
Лекции / Лекци3
.docЛекция 3
Пиростатика.
Изучает горение пороха в постоянном объеме. Позволяет изучить влияние формы, размеров, природы пороха условий заряжания, давления пороховых газов на интенсивность газообразования.
Горение пороха.
Зажигание – начало горения под влиянием внешнего импульса (быстрый нагрев, удар). tвозгор= 2000C (бездымные); 3000 (дымные).
Воспламенение – по поверхности (шероховатая, гладкая).
Горение – вглубь зерна.
На открытом воздухе бездымные пороха воспламеняются в 2 – 3 раза быстрее, чем горят (Uв=2 – 4 мм/c ; u=10 мм/c).
Горение бездымного пороха параллельными слоями.
- основное отличие от бризантных ВВ.
Открыл Вьель(при =const, 2/1)=e”1/e’1). Закон назван геометрическим. В его основе допущения:
-
масса однородна по химической природе и физическим свойствам (структура, , размер)
-
воспламенение мгновенно
-
горение параллельными слоями с одинаковой линейной скоростью
Закон скорости горения.
Закон скорости горения - это основная зависимость ВБ.
С
Выражение закона
(функциональная зависимость)
И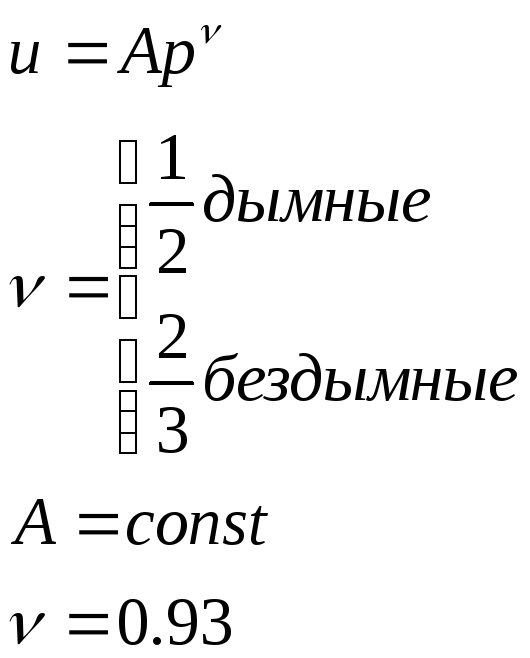 звестен
ряд эмпирических зависимостей. Получают
сжиганием пороха в бомбе и обработкой
кривой P(t).
звестен
ряд эмпирических зависимостей. Получают
сжиганием пороха в бомбе и обработкой
кривой P(t).
-
Закон Вьеля:
По Забудскому.
-
З
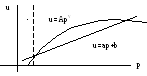 акон
Вуколова и Граве:
акон
Вуколова и Граве:
400 кг.см2
u=ap+b; a, b – const;
-
Закон Дроздова, Шмица:
u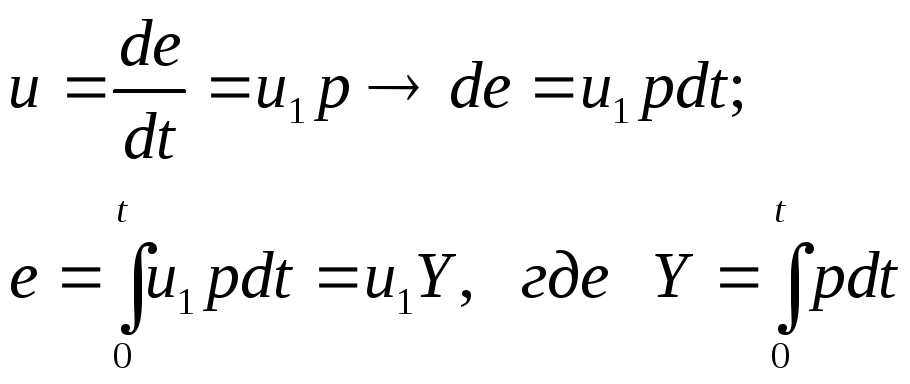 =A1p
или
u=u1p;
u1
– константа скорости горения (скорость
горения при 1 атм).
=A1p
или
u=u1p;
u1
– константа скорости горения (скорость
горения при 1 атм).
- импульс давления ПГ.
Д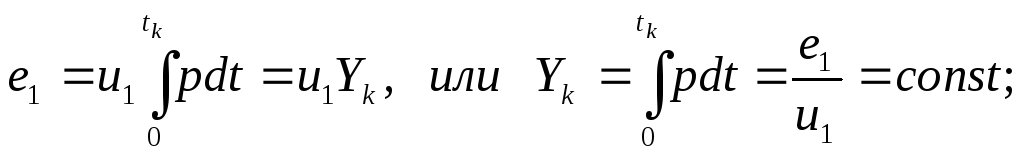 ля
конца горения e=e1,
t=tk:
ля
конца горения e=e1,
t=tk:
Т.е. Yk=Yk(e1,u1) и YkYk();
Н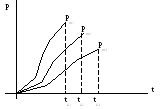 о
кривые P(t)
ведут себя
по разному.
о
кривые P(t)
ведут себя
по разному.
П
Получено
экспериментально.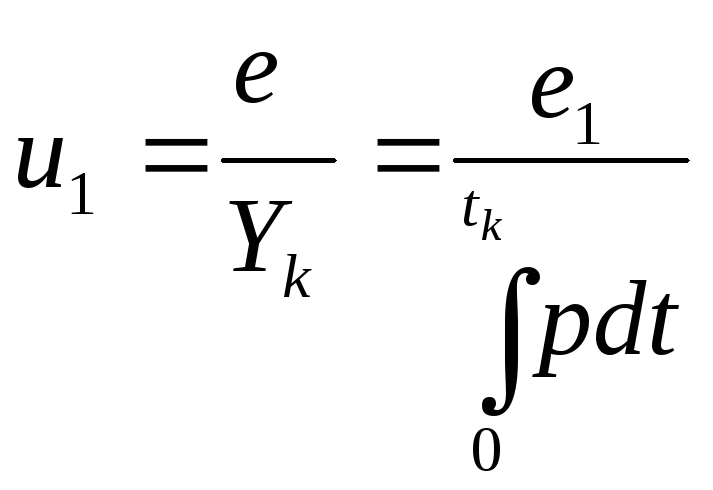
Быстрота газообразования.
Для управления процессом выстрела надо регулировать газоприток.
О
Относительная
часть сгоревшего заряда или относительный
объем.![]()
’ – объем сгоревшего пороха (’=r/) 1 – начальный объем заряда (1=/), тогда r=; ’=1;
d/dt – быстрота газообразования (объемная скорость горения).
(d/dt) – секундный массовый приток; (d/dt) – секундный приток энергии, определяет характер нарастания давления. Т.к. , - const важно знать зависимость d/dt от всех факторов. Выведем:
П
1
S1


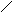

ост



de



e



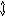
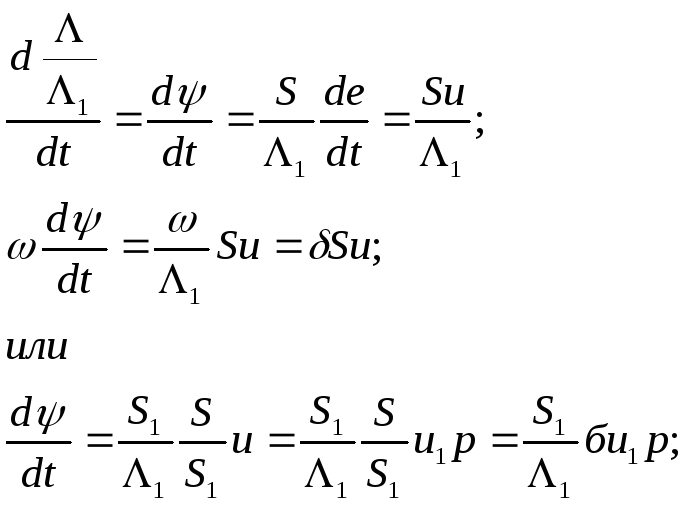
О
- Массовая скорость
газообразования.
S1/1 –начальная «оголенность» (начальная уд. поверхность пороха).
S/S1= - относительная поверхность горения.
Д
- Объемная скорость
газообразования.![]() ля
данной природы пороха (u1=const).
Можно меняя форму и размер изменять
газоприток.
ля
данной природы пороха (u1=const).
Можно меняя форму и размер изменять
газоприток.
Su1- объем ПГ, образующихся в единицу времени при p=1 атм.
S![]() u1/1
– удельная
интенсивность газообразования отнесенной
к p=1
атм.
– ее
обозначим через Г:
u1/1
– удельная
интенсивность газообразования отнесенной
к p=1
атм.
– ее
обозначим через Г:
Когда =1 Г=Г1=(S1/1)u1 – начальная удельная интенсивность газообразования (живучесть пороха) или острота отнесенная к p=1 атм.
Если - порох прогрессивной формы.
Если - порох дегрессивной формы.
Связь между геометрией пороха и образованием газов.
Рассмотрим порох дегрессивной формы ().
Обозначим: e1; e; z=e/e1 – относительная толщина сгоревшего пороха.
=/1; =S/S1.
Во время горения 01; от 1 до k<1.
Используя основные положения геометрического закона, выведем зависимости (z); (z); (); S1/1.
Для всех форм порохов справедливо: (z)=z(1+z+ z2) – на основе исследований.
Где , , =const – формы.
Для ленточного пороха:
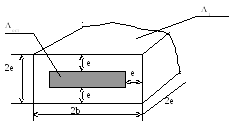
сг – объем сгоревшей части.
 ост
– объем оставшейся части.
ост
– объем оставшейся части.
Введем характеристики растянутости ленты:
2e1/2b=e1/b=<1 – относительное уменьшение ширины за t горения.
2e1/2c=e1/c=<1 – относительное уменьшение длины за t горения.
Т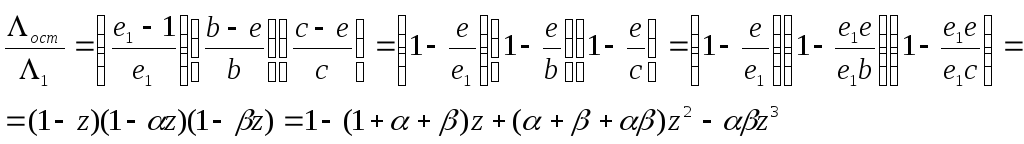 огда:
огда:
Подставим в =1-(ост/1) получим:
=(1++)z-((++)z2 +z3
если вынесем 1ый - член за скобки и обозначим:
в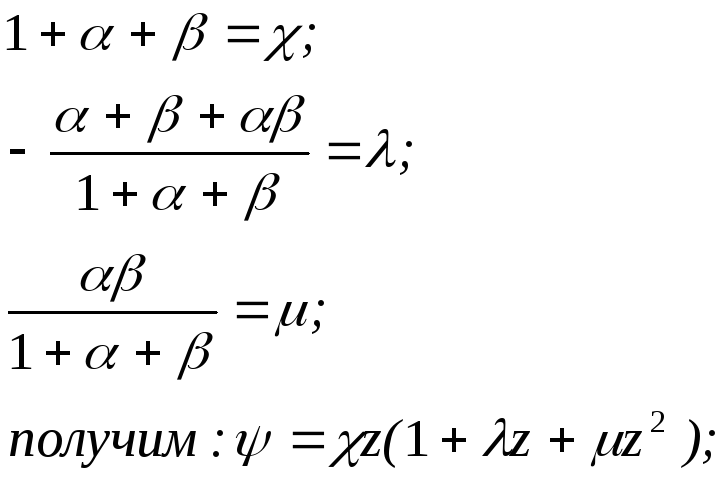 конце горения:
zk=1;k=1
1=(1++);
конце горения:
zk=1;k=1
1=(1++);
численные характеристики , , должны удовлетворять этому равенству (служит для проверки расчетных характеристик).
Рассмотрим некоторые формы порохов:
-
Т
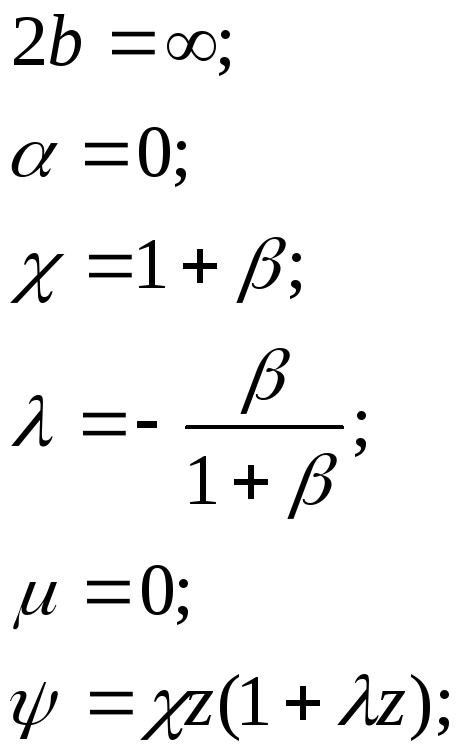
Лента бесконечной длины.
рубка:
Диаметр не влияет.
-
Л
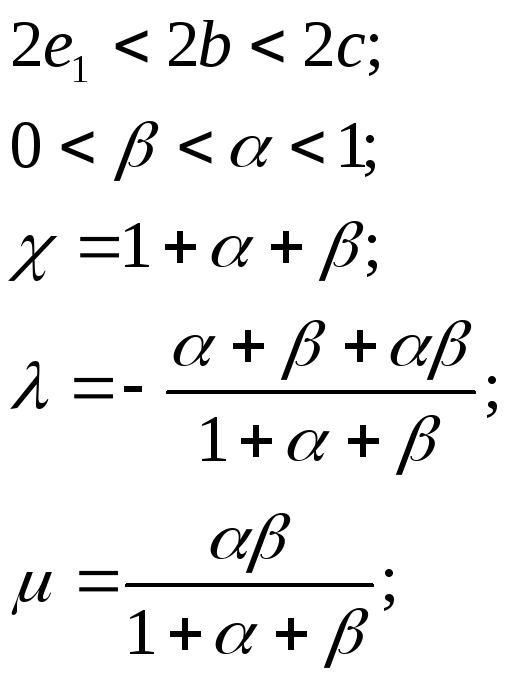
Длина > ширины
ента:
-
К
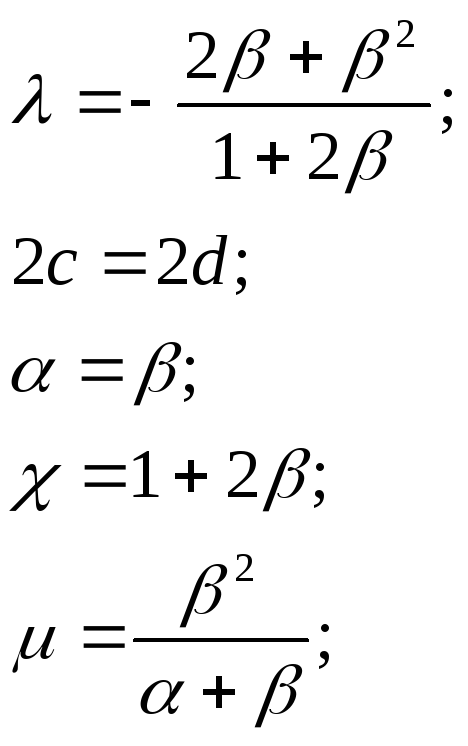 вадратная
пластинка:
вадратная
пластинка:
-
К
 вадратный
брусок:
вадратный
брусок:
-
К
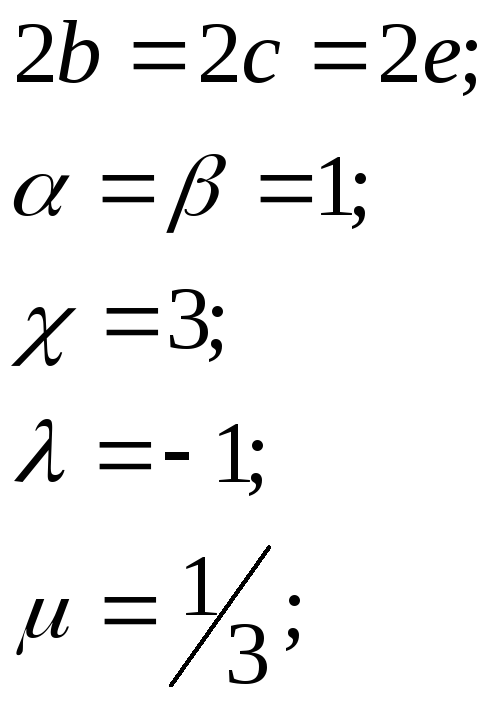 уб:
уб:
Зависимость для = S/S1:
Выше было получено =z(1+z+z2); т.к. d=Sde и S=d/ то для (z) возьмем:
d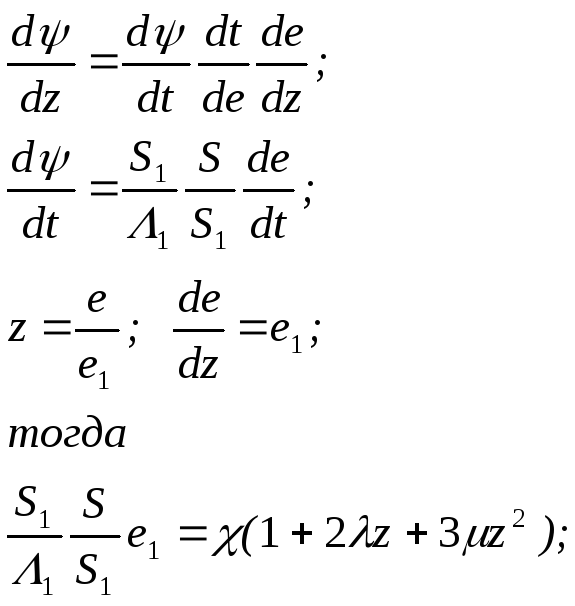 /dz=(1+2z+32);
подставим:
/dz=(1+2z+32);
подставим:
д
(1)![]()
В начале горения при z=0; 0=1; в конце горения k=1+2+3;
Для начала оголения S1/1=/e1; зависит от формы зерна () и от размеров (e1).
Подставим в (1) d/dz=; (d/dz)0=.
И![]() спользуя
полученные зависимости, формулу для Г
можно представить:
спользуя
полученные зависимости, формулу для Г
можно представить:
Где S1/1=(/e1); (S/S1)=;
В зависимости от характера изменения S или пороха делятся на две группы:
Дегрессивной формы d/dt<0;
Прогрессивной формы d/dt>0;
Г
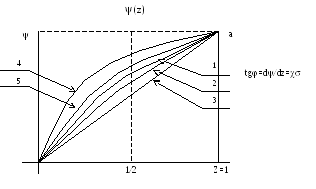 рафики
(z)
и (z)
называют
листами прогрессивности.
рафики
(z)
и (z)
называют
листами прогрессивности.
Характеристики порохов дегрессивной формы.
№ |
Форма пороха |
|
|
k |
1 |
Труба |
1.00 |
0 |
1.00 |
2 |
Лента |
1.06 |
-0.06 |
0.88 |
3 |
Кв. Пластина |
1.20 |
-0.20 |
0.67 |
4 |
Кв. Брусок |
2.00 |
-1.0 |
0 |
5 |
Куб |
3.00 |
-1.0 |
0 |
Д вучленная
зависимость (z).
вучленная
зависимость (z).
1
2
3
4
5
z=0; z=1/2; z=1.
z=0; =0;z=1/2; /2(1+(2)+( /4))=1/2(1+1/2); z=1; 1=(1++)=1(1+1).
Решая систему получим:
1=-(/2)=(1-/2)=1++-(/2); 1=Y1-1 и 11=1-1=-(+-/2).
При двучленной зависимости =1+21z; =1z(1+1z);
И сключая
из формулы z
получим:
сключая
из формулы z
получим:
