3. Квазилинейные факторы и формулы Карлемана

Использование нелинейных одномерных моделей данных (кривых) принципиально не отличается от использования линейных моделей (прямых). Предлагается использовать квазилинейные модели, допускающие простые явные формулы обработки данных и опирающиеся на описанный алгоритм построения линейных моделей.

Пусть, как и в случае линейных моделей, задана таблица с пропусками A. Построение квазилинейных моделей, наилучшим образом приближающих данные, предлагается проводить в несколько этапов.

Построение линейной модели – решение задачи (1). Для определенности полагаем, что (y,b)=0, (y,y)=1 – этого всегда можно добиться.

Интерполяция (сглаживание)

Строится вектор-функция f(t), минимизирующая функционал:

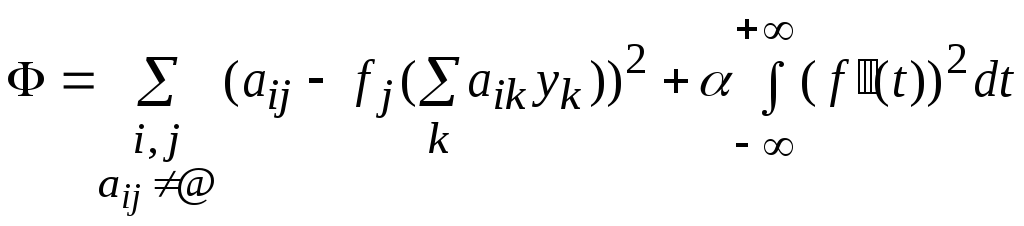, где>0 – параметр сглаживания.

При этом решение задачи сглаживания дается либо одним полиномом, либо кубическими сплайнами.

Экстраполяция

Вектор-функция f(t) экстраполируется при помощи касательных.

Сглаженная вектор-функция f(t) экстраполируется с некоторого конечного множества{t_k} (которое не обязательно связано с проекциями на прямуюz_j=ty_j+b_j исходных строк данных) на всю вещественную прямую с использованием формул Карлемана [1] (с помощью формул Карлемана экстраполируется отклонение кривойf(t) от прямойty+b).

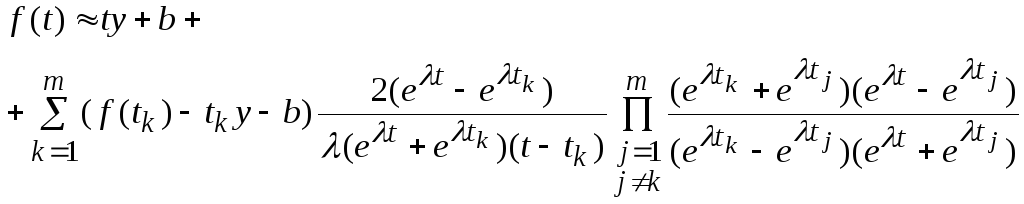, (5)

где – параметр метода, характеризующий, насколько широка полоса на плоскости комплексных чисел, в которой гарантированно голоморфна экстраполируемая функция (эта ширина равна).

Интерполяция со сглаживанием

При решении задачи интерполяции со сглаживанием необходимо нормировать значения x_i иa_ij таким образом, чтобы они лежали в отрезке[-1,1]. В последствии, при вычислении значения функции, полученные значения денормируются.

Интерполяция полиномом степени n

В случае аппроксимация полиномом степени n ставится задача наилучшего приближения матрицыA полиномами вида , т.е.:

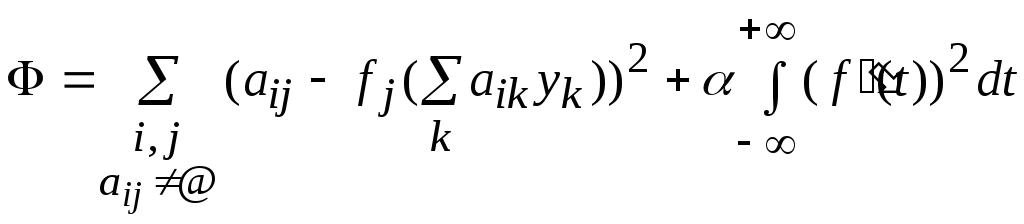, где>0 – параметр сглаживания.

Так как значения x_i=(a_i,y), гдеa_i–i-ая строка матрицыA, фиксированы (вычислены на предыдущем этапе), то значения коэффициентов полинома(k=0..n), доставляющие минимум функционалу, определяются из системы равенств(k=0..n) следующим образом:

Вычислим значение интеграла при параметре сглаживания:

,, тогда:

. Следовательно, интеграл будет равен (учитывая, что искомая функция определена на отрезке[-1,1]):

.

Тогда: .

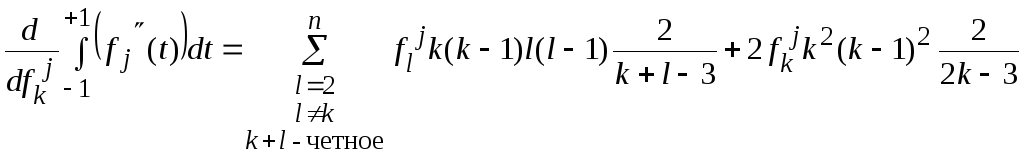Окончательно, для k=0..n, имеем:

.

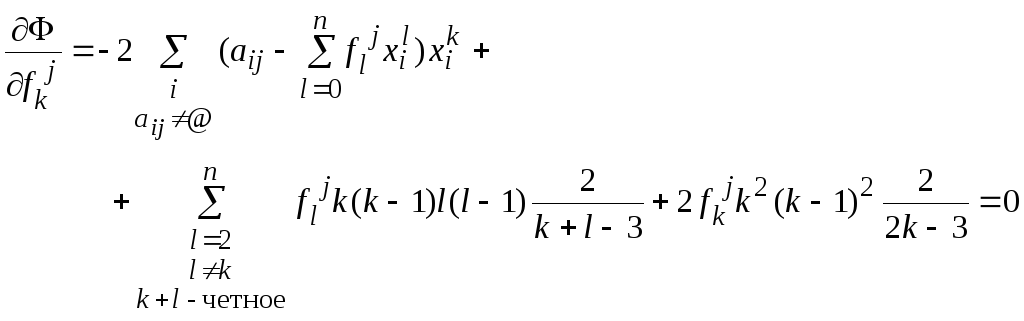Группируя коэффициенты при (k=0..n), получим:

, дляk=0..n, где:

,

.

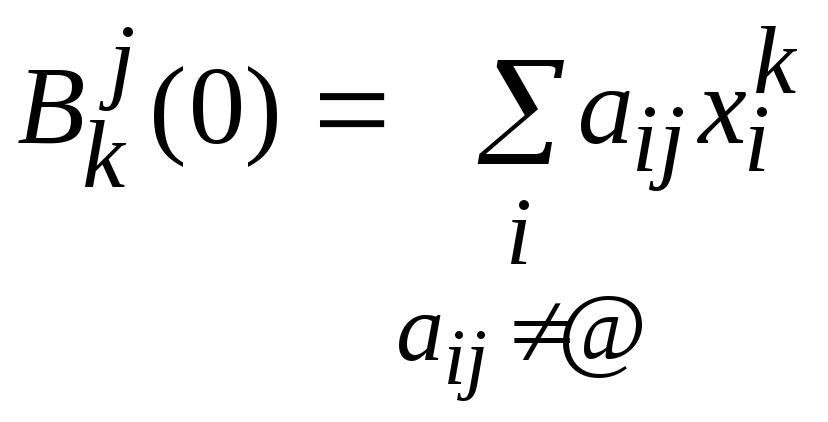Возьмем 1-ое уравнение,выразим через оставшиеся и подставим полученное выражение во все остальные уравнения системы:

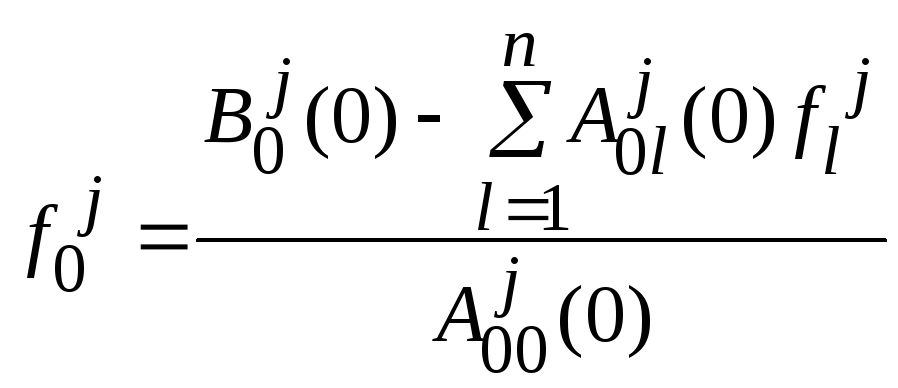. Отсюда получаем:

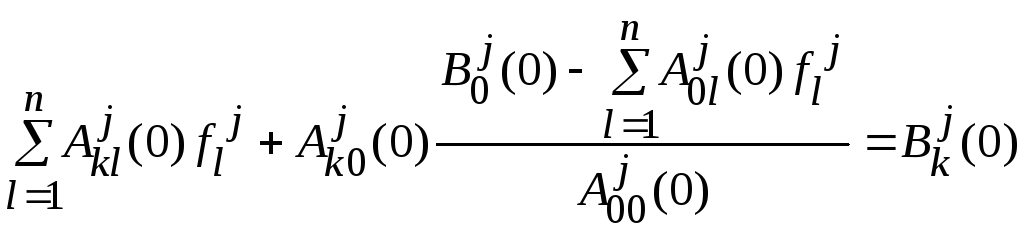дляk=1..n,

, дляk=1..n.

Эту систему можно записать в следующем виде:

, дляk=1..n,где,

.

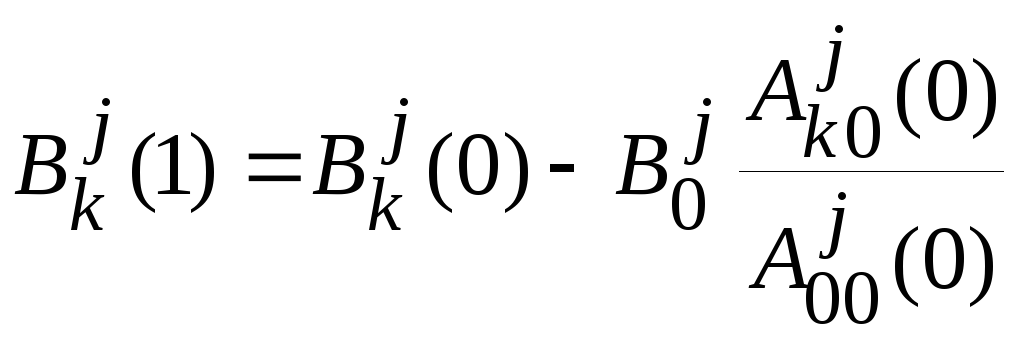Теперь аналогичным образом исключаем и т.д.

Пусть m таких исключений уже сделано, тогда имеем систему:

, дляk=m..n. Аналогично описанному выше из первого уравнения системы (k=m) выразими подставим в оставшиеся уравнения. В итоге получим:

,

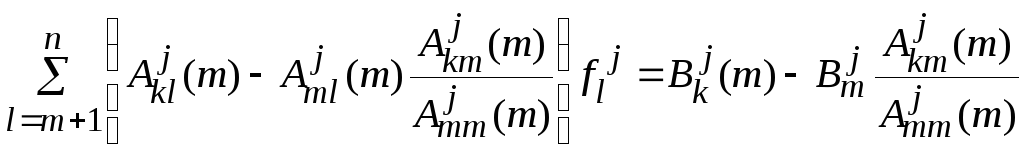, дляk=m+1..n. Следовательно:

, дляk=m+1..n, где

,.

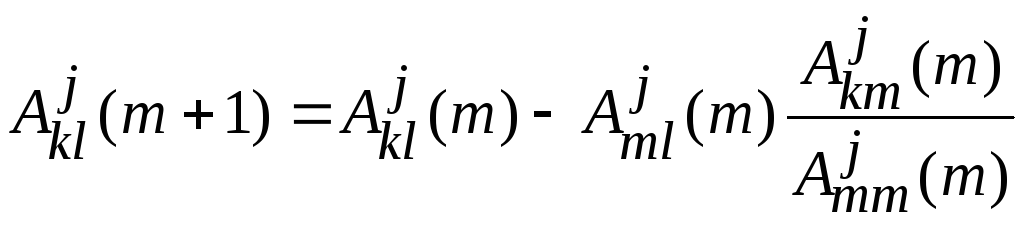Таким образом, для нахождения (k=0..n) получили следующие рекуррентные соотношения:

,,

,,

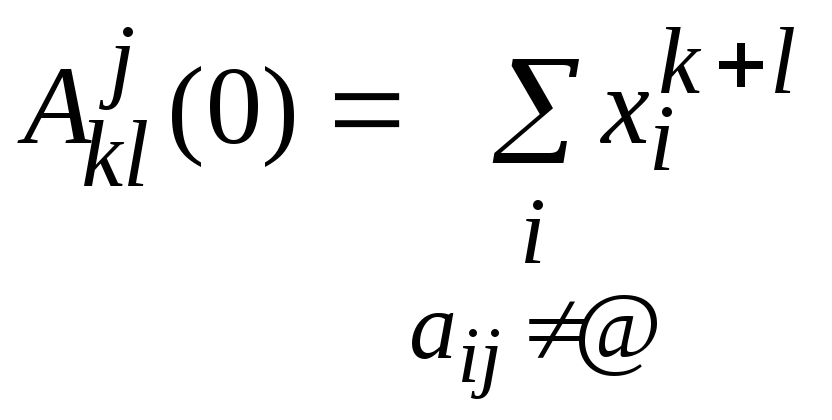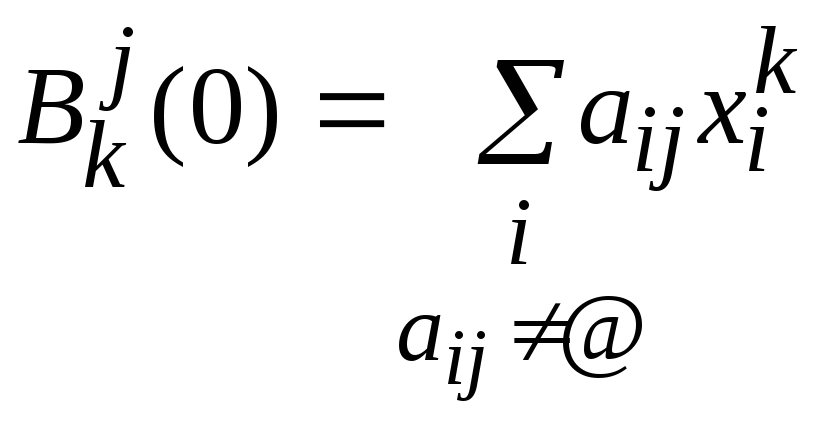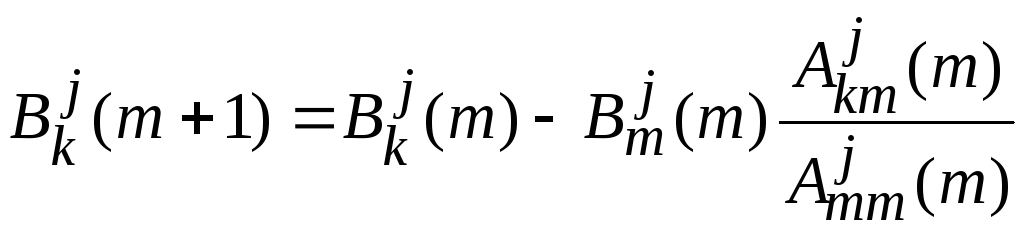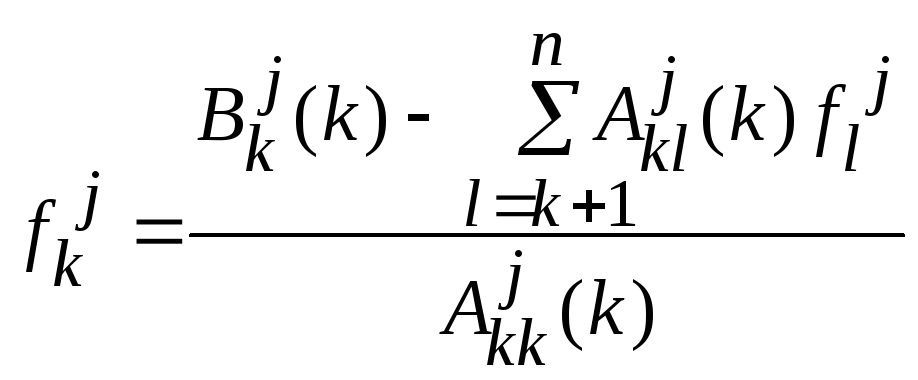, дляk=n..0.

Интерполяция кубическими сплайнами

Требуется решить с использованием кубических сплайнов следующую задачу сглаживания:

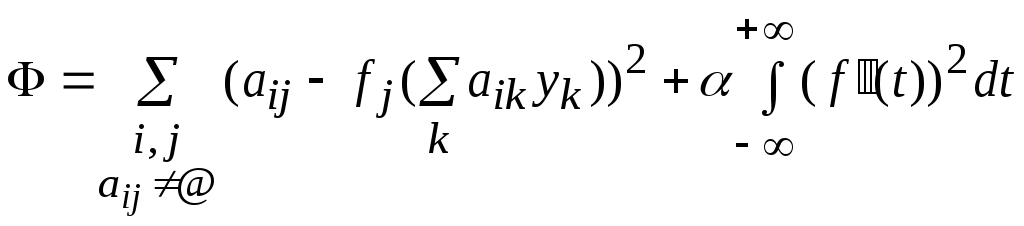, где>0 – параметр сглаживания.

При решении этой задачи имеем отрезок [-1,1]. Разобьем его на n частей точками ,s=0..n, где:. При этом:.

Пусть , где,s=1..n, тогда имеем:

.

Посчитаем производные:

,.

Значение интеграла при коэффициенте гладкости:

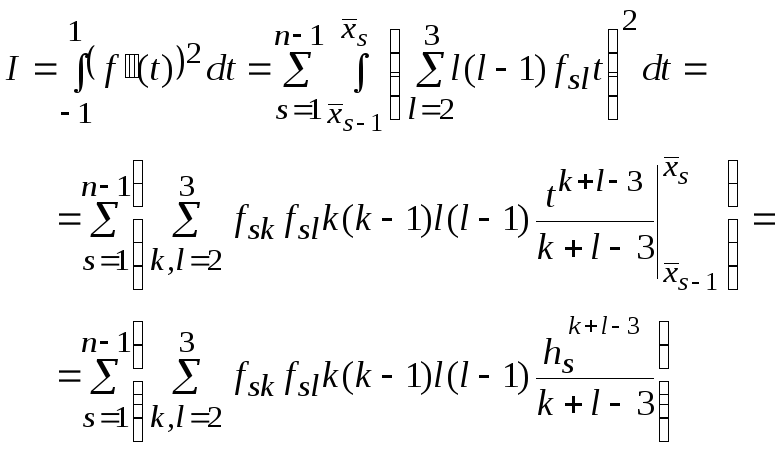
Таким образом, исходная задача сглаживания запишется в следующем виде:

=H+Imin, где

,.

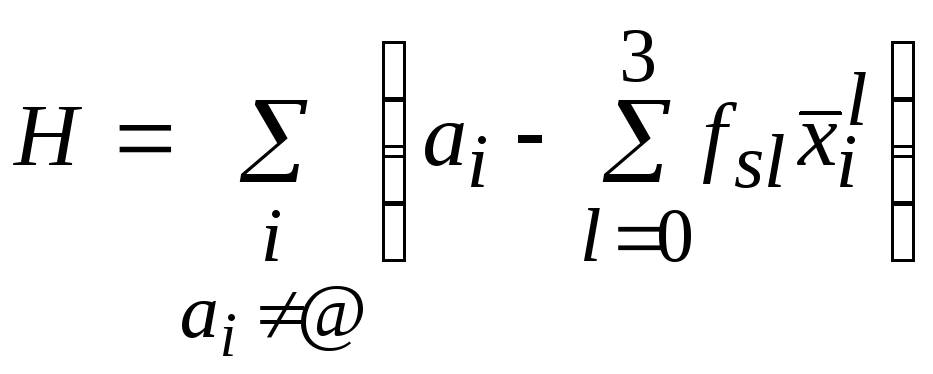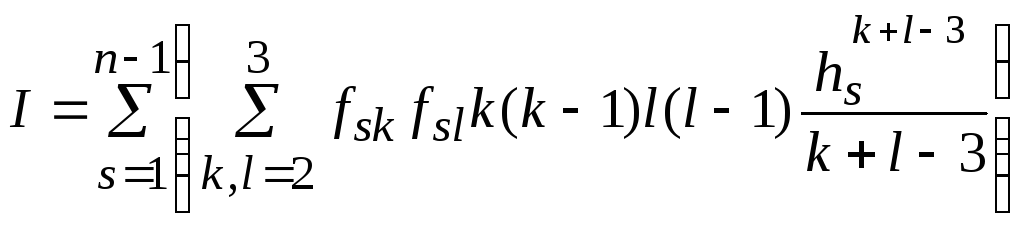Полученная сплайн-функция должна быть непрерывная в узлах сетки вместе со своей первой и второй производной.

Поэтому из условий непрерывности получим следующую систему:

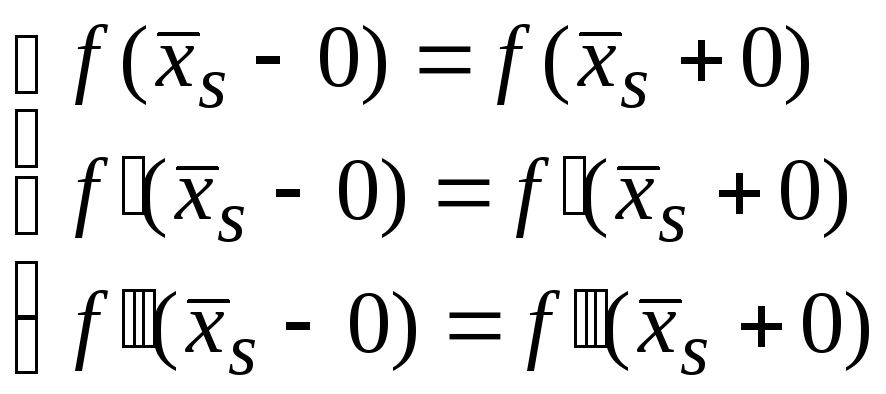, гдеs=1..n-1.

Подставив соответствующие значения, получим условия на коэффициенты сплайнов:

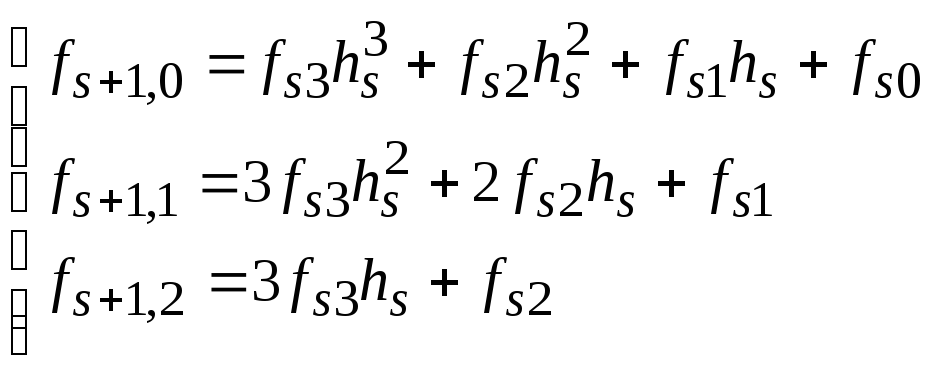, гдеs=1..n-1.

Исходная задача сглаживания решается методом множителей Лагранжа:

, где:

, приs=1..n, – линейные ограничения, полученные из условий непрерывности.

Нужно решить следующую систему:

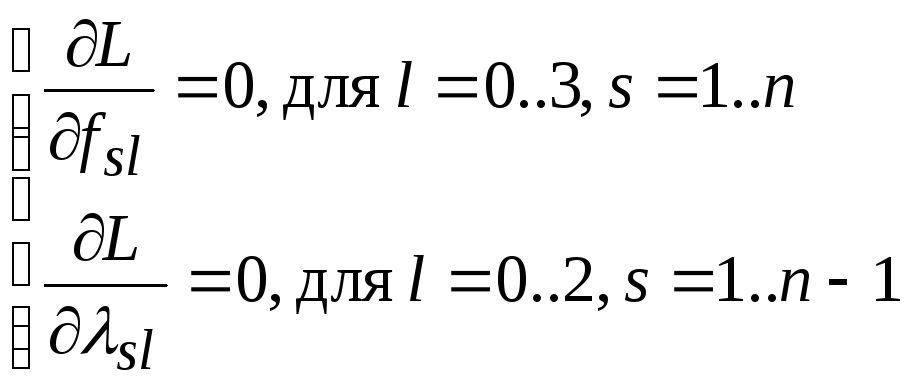, т.е. систему из (7n-3) уравнений и с (7n-3) неизвестными.

Первые строчки этой системы можно расписать следующим образом:

, где:

,,

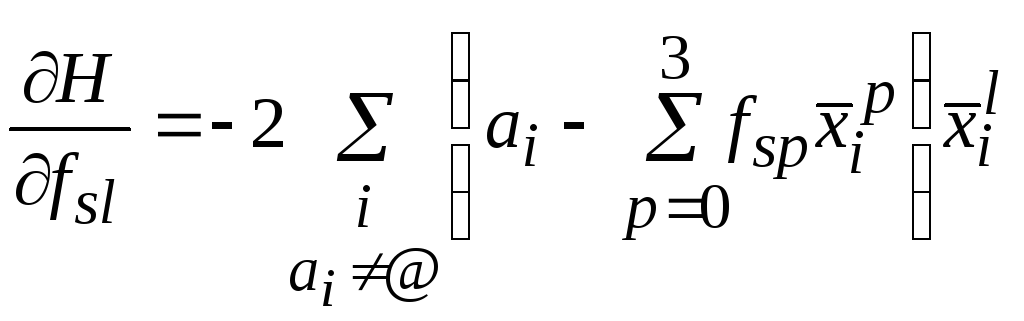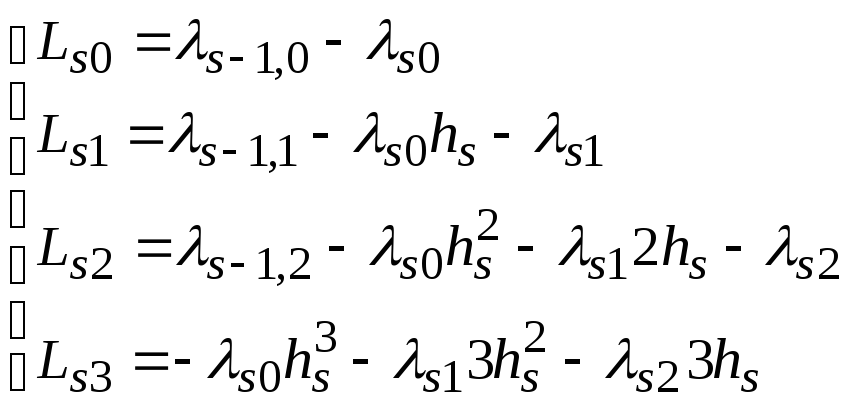, при этом коэффициенты с индексомs-1берутся дляs=2..n, коэффициенты с индексомs берутся дляs=1..n-1.

Подставив все это в исходную систему, можно заметить, что она имеет практически блочно-диагональный вид, где размер отдельных блоков достаточно мал, поэтому, несмотря на большой размер ((7n-3)(7n-3)), она с хорошей точностью решается методом Гаусса.

Экстраполяция

Необходимость в экстраполяции вызвана двумя обстоятельствами: во-первых, построенная на втором этапе сглаженная зависимость в принципе интерполяционная и не может быть экстраполирована, во-вторых, в ней фактически содержится в явном виде информация о каждой строке матрицы данных. Сглаживание просто многочленом небольшой степени по методу наименьших квадратов свободно от второго недостатка (информация "сворачивается" в несколько коэффициентов), но также не дает хорошей экстраполяции.

Экстраполяция прямыми

При экстраполяции прямыми полученная функция экстраполируется с отрезка [-1,1]на всю вещественную ось за счет добавления касательных к функции в концах отрезка.

Экстраполяция при помощи формул Карлемана

С помощью формул Карлемана экстраполируется отклонение кривой f(t) от прямойty+b. Формулы Карлемана обеспечивают хорошую экстраполяцию аналитических функция на всю прямую (конечно, строго говоря, в каждом конкретном случае нет гарантий, что именно по формуле (5) будет получена наилучшая экстраполяция, однако существует ряд теорем о том, что формула (5) и родственные ей дают наилучшее приближение в различных классах аналитических функций[1]).

Последовательность квазилинейных факторов

Точка на построенной кривой f(t), соответствующая полному ("комплектному") вектору данныхaстроится какf((a,y)), в этом и заключается квазилинейность метода: сначала ищется проекция вектора данных на прямую Pr(a)=ty+b,t=(a,y), затем строится точка на кривойf(t). Также и для неполных векторов данных – сначала ищется точка на прямой по формуле (3), а затем – соответствующая точка на кривойf(t) приt=t(a).

После построения кривой f(t) данные заменяются на уклонения от модели. Далее снова ищется наилучшее приближение видаx_iy_j+b_jдля матрицы уклонений, вновь строится сглаживание, потом – экстраполяция по Карлеману и т.д., пока уклонения не приблизятся в достаточной степени к нулю.

Действуя по этой схеме, для таблиц данных с пропусками A=(a_ij) получаем последовательность уклонений , таблиц(для определенности полагаем (y^q,b^q)=0, (y^q,y^q)=1 – этого всегда можно добиться) и кривыхf^q(t).

Это последовательности связаны следующим образом:

,– наилучшее приближение такого вида (решение задачи (1)) для таблицы,

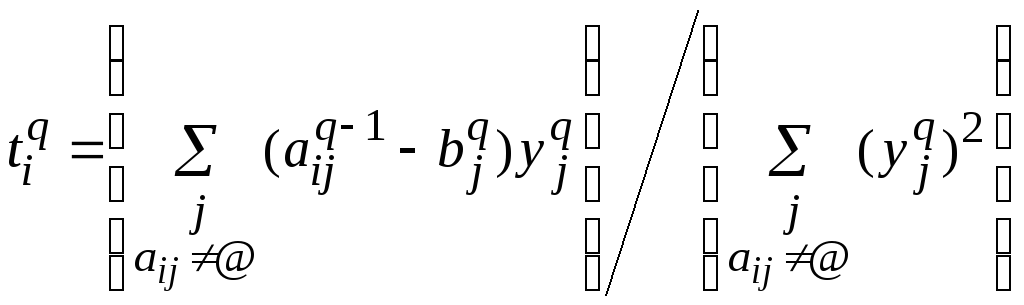, (6)

кривая f^q(t) получается в два этапа: сглаживается зависимость, заданная на конечном множествеследующим образом:, еслии, если, – после чего сглаженная зависимость экстраполируется с помощью формул (5). Последовательность уклонений определяется с помощью кривойf^q(t) и значений:.

В результате исходная таблица предстает в виде . Еслиa_ij@, то эта формула аппроксимирует исходные данные, если же, то она дает способ восстановления данных. Большой интерес вызывает вопрос: сколько слагаемых следует брать для обработки данных? Существует несколько вариантов ответов, но большинство из них подчиняется эвристической формуле:число слагаемых должно быть минимальным среди тех, что обеспечивают удовлетворительное (терпимое) тестирование метода на известных данных.

Алгоритм применим в том случае, когда матрица данных не может быть приведена перестановкой строк и столбцов к следующему блочно-диагональному виду:

, (7)

где 0 – прямоугольные матрицы с нулевыми элементами.

Приведенный алгоритм заполнения пробелов не требует их предварительного априорного заполнения – в отличие от многих других алгоритмов, предназначенных для той же цели. Однако же он требует предварительной нормировки ("обезразмеривания") данных – перехода в каждом столбце таблицы к "естественной" единице измерения. Чаще всего производится нормировка на единичное среднеквадратичное уклонение в столбцах или на единичный разброс данных в каждом столбце (если нет каких-либо специфических ограничений, связанных со смыслом задачи).