6. Среднеквадратические оценки погрешностей весов синапсов

Перейдем теперь к оценке среднеквадратических отклонений погрешностей весов синапсов. Предполагаем, что погрешности весов синапсов являются независимыми случайными величинами. При этом можно налагать менее жесткие ограничения при вычислении погрешностей весов синапсов и сигналов сети.

Нам задана – допустимая погрешность выходного сигнала сети. Будем рассматривать ее как величину среднеквадратического отклонения погрешности выходного сигнала сети.

Выходной сигнал сети одновременно является выходным сигналом нелинейного преобразователя. Поэтому, зная величину среднеквадратического отклонения погрешности выходного сигнала , мы можем вычислить среднеквадратическое отклонение погрешности входного сигнала нелинейного преобразователя методом обратного распространения точности. Среднеквадратическое отклонение погрешности входного сигнала вычисляется по формуле:, где– функция активации нелинейного преобразователя,A – его точный входной сигнал.

Среднеквадратическое отклонение погрешности входного сигнала нелинейного преобразователя , в свою очередь, является одновременно среднеквадратическим отклонением погрешности выходного сигнала сумматора. Дисперсия выходного сумматора равна.

Зная дисперсию выходного сигнала сумматора, мы можем вычислять среднеквадратические отклонения погрешностей весов синапсов и входных сигналов сумматора.

Как и для интервальных оценок, получим формулы для пропорционального и равномерного распределения среднеквадратических отклонений погрешностей по входам сумматора.

Предварительно заметим, что математические ожидания случайных величин иравны нулю. Случайные величиныиявляются независимыми, поэтому

.

Выясним сначала, как вычисляются среднеквадратические отклонения погрешностей для пропорционального распределения.

Как было показано для интервальной оценки погрешностей, при пропорциональном распределении получили формулу . Рассмотрим дисперсию обеих частей этого неравенства:

.

Отсюда получаем .

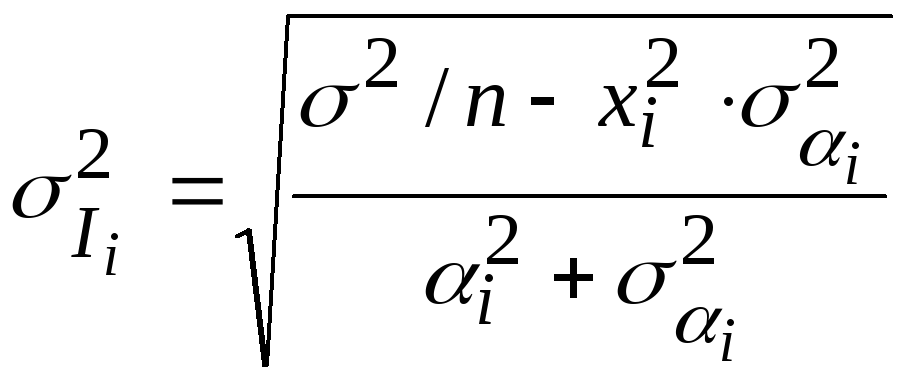В этой формуле две неизвестных величины: и. Чтобы вычислить, требуется присвоить некоторое значение величине. Представим. Тогда числитель подкоренного выражения можно представить в виде. Нам требуется, чтобы числитель был положительной величиной. Поэтому следует выбрать. Выбирая такое, мы определяеми можем вычислить. Мы получили формулу для пропорционального распределения среднеквадратических отклонений погрешностей.

Дисперсия выходного сигнала сумматора равняется . Как было показано выше, погрешность выходного сигнала сумматора складывается из погрешностей сигналов и весов синапсов:. Рассмотрим дисперсию этой суммы:

=

==

==

=.

Предполагаем, что дисперсии погрешностей входных сигналов сумматора равны между собой и дисперсии погрешностей его весов синапсовравны между собой.

Вычислим среднеквадратическое отклонение погрешностей входных сигналов сумматора:

В этой формуле две неизвестных величины: и. Чтобы вычислить, требуется задать некоторое значение величинетак, чтобы числитель был положительной величиной. То есть следует выбрать. Выбирая такое, мы определяеми можем вычислить. Мы получили формулы для равномерного распределения среднеквадратических отклонений погрешностей.

Таким образом, мы можем вычислить среднеквадратические отклонения погрешностей весов синапсов и входных сигналов сумматора. Вычислив эти отклонения для одного слоя, можно переходить к предыдущему слою и т.д.

Как и в случае интервальных оценок, выбор на каждом шаге достаточно произволен. Если вычисленные среднеквадратические отклонения погрешностей для данного слоя по каким-то причинам нас не устраивают, можно вернуться на предыдущий слой, выбрать другоеk, удовлетворяющее накладываемому на него условию, и вычислить новые величины для погрешностей.

Вообще говоря, вычисленные допустимые погрешности весов синапсов могут достаточно сильно отличаться как в разных слоях, так и внутри одного слоя. Если требуется, чтобы погрешности весов синапсов имели достаточно близкие значения, можно попытаться выровнять их за счет итерационного вычисления погрешностей весов синапсов. То есть мы уменьшаем допустимые погрешности весов синапсов последних слоев сети. За счет этого должны увеличиться допустимые погрешности первых слоев сети. Если при этом допустимые погрешности первых слоев сети получились больше, чем допустимые погрешности последних слоев, то увеличиваем допустимые погрешности последних слоев сети. Итерации повторяются до тех пор, пока полученные результаты нас не устроят.