Порядок проведения работы:

1. Теоретически определить резонансные частоты и формы колеблющейся балки. Для теоретического расчета используется численный алгоритм (см. главу 3).

2. Провести эксперимент и проанализировать результаты.

2.1. Собрать схему установки (см. рис. 2, 3, 4).

2.2. Доложить преподавателю о готовности к работе.

КАТЕГОРИЧЕСКИ ЗАПРЕЩАЕТСЯ ВКЛЮЧАТЬ СХЕМУ И ОТДЕЛЬНЫЕ ПРИБОРЫ БЕЗ РАЗРЕШЕНИЯ ПРЕПОДАВАТЕЛЯ!

2.3. Снять амплитудно-частотные характеристики для двух различных балок в диапазоне частот от 0 до 300 Гц.

2.4. Произвести наблюдение форм колебаний балки с применением стробоскопического метода.

2.5. Графически представить результаты эксперимента и сравнить их с теоретическими значениями.

Контрольные вопросы:

1. Приведите уравнение вынужденных изгибных колебаний балки постоянного поперечного сечения.

2. Какими методами можно получить решение задачи о вынужденных изгибных колебаниях балки (системы с распределенными параметрами)?

3. Какие экспериментальные методы используются для измерения частоты колебаний механических систем?

4. Как строится амплитудно-частотная характеристика системы?

3. Метод парабол отыскания корней алгебраических и трансцендентных уравнений

Метод парабол [3] предназначен для приближенного решения уравнения вида

f(z)=0 , (21)

г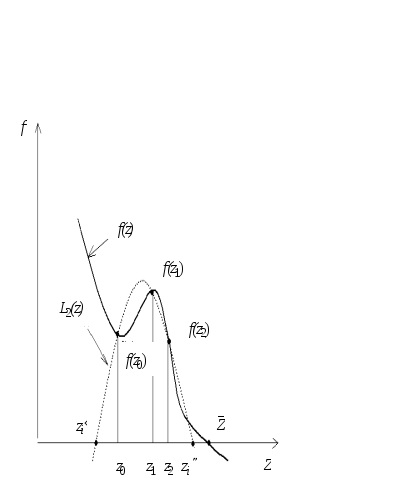деf(z)  заданная функция действительного или комплексного аргумента, позволяет находить все корни уравнения (21) без знания их начальных приближений (см. рис.5). Необходимо уточнить, что функция f(z) может быть задана в виде алгоритма, позволяющего вычислять значение f по заданному аргументу z, аналитический вид не требуется.

Рис. 5.

Исходя из некоторых трех точек z₀, z₁, z₂ строится интерполяционный полином Лагранжа второй степени (парабола). Один из корней этого полинома z_i выбирается в качестве приближения, и организуются новые три точки (z₀, z₁, z_i). По ним опять строится полином и определяются его корни. Доказано, что такая последовательность сходится к корню уравнения (21). На рис.5 графически изображено одно приближение в методе парабол;  корень уравнения, и корни полинома Лагранжа L₂(z).

Полином L₂(z) для i-го приближения имеет вид

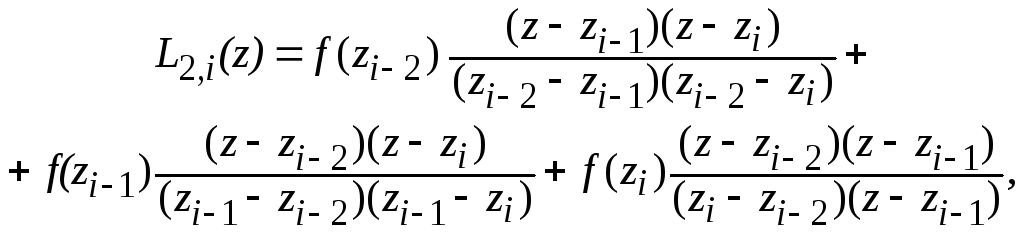(22)

где .

Точка z_i+1 определяется как ближайший к z_i корень уравнения . Для более удобной формы записи введем обозначения:

, ,,,, (i = 2, 3,…). (23)

Тогда соотношение (22) относительно новой переменной  запишется так:

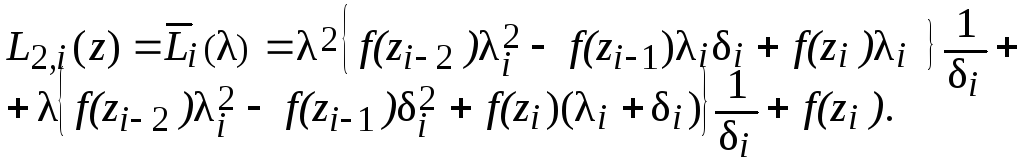(24)

Корни квадратного трехчлена (24) относительно  будут иметь следующий вид:

(25)

где .

В (25) знак перед фигурной скобкой, чтобы модуль знаменателя был наибольшим, тогда

. (26)

При реализации на ЭВМ точность определения корня уравнения задается по формуле

, (27)

где наперед заданное положительное число, определяющее требуемую точность вычислений.

Сходимость метода парабол доказана, если начальные значения z₀, z₁, z₂ находятся в достаточно малой окрестности корня уравнения (21). Но большой практический опыт применения метода показал, что последовательность всегда сходится к некоторому корню уравнения (21) независимо от выбораz₀, z₁, z₂. Если z₀=-1, z₁=1, z₂ = 0, то последовательность сходится к наименьшему по модулю корню.

После того, как найден корень уравнения, требуется его выделить и приступить к отысканию следующего. Эту процедуру можно осуществить с помощью неявной схемы Горнера. Для определения второго корня уравнения, вместо исходного уравнения (21), рассматривается

,

где z₁  первый корень уравнения, затем

,

и так далее.

Укажем очевидные преимущества метода парабол:

1. Не требуется знание начальных приближений корней.

2. В методе необходимо вычислять только значения функции (большинство методов требуют вычисления производных).

3. Если приближение выбрано симметрично относительно начала координат, то корни определяются в порядке возрастания.