28. Замена переменных в двойном интеграле. Пример: случай полярных координат.

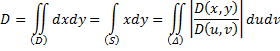
Вычислим интеграл , используя замену переменных . Рассмотрим интеграл как предел интегральных сумм. Область (D) сеткой кривых разделяется на частичные области D_i, внутри каждой частичной области берём произвольные точки (x_i, y_i). Составляем интегральную сумму: , где D_i – площадь i-ой частичной области. Устремим максимальный диаметр к нулю: . По определению, . Совершим замену переменных (*). При замене (*) площадь .

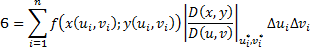
Если , то и , следовательно,

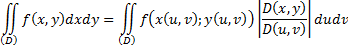
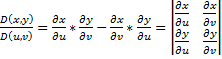– якобиан преобразования (*).

П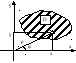ример с полярными координатами.

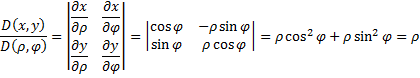
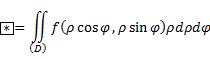
29. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.

Замена переменных в тройном интеграле в общем случае.

Пусть имеется тело (V) с границей (S).

Пусть , тогда .

Замена: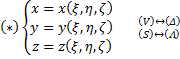

П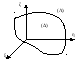реобразование (*) будем считать взаимно-однозначным, то есть всё можно выразить друг через друга, а именно: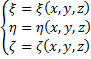

Пусть поверхность (Λ) задаётся параметрически, то есть:

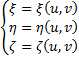
Получаем параметрическое задание поверхности (S) (см. рис. ниже).

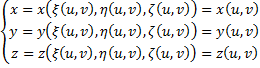
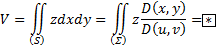
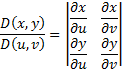
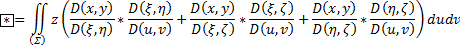
Два последних двойных интеграла равны, так как: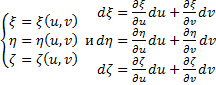

Применим к последнему выражению формулу Гаусса-Остроградского, то есть эту формулу: .

Пусть ,,, тогда:

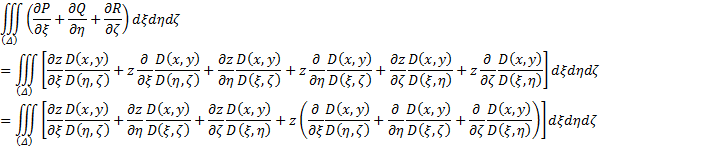
Выражение в скобках равно нулю. Оставшееся выражение запишем так:

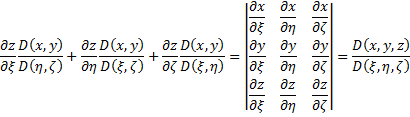
Это якобиан преобразования. Окончательно получаем:

А для общего случая:

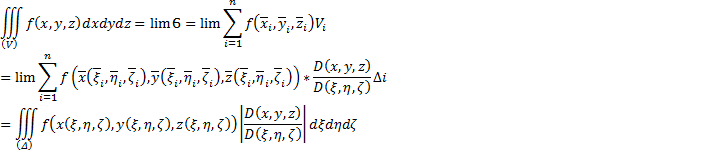
Цилиндрические координаты:

Переходим от координаты M(x,y,z) к M(ρ,φ,z). Это цилиндрические координаты, где: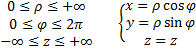

Получаем, что .

Сферические координаты:

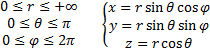
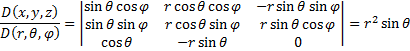
Получаем элемент объёма сферических координат: .

30. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.

Рассмотрим кусок поверхностиS, заданной уравнением F=(x,y,z)=0. Пусть выполняется условие , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором . Разобьем поверхность S сеткой гладких кривых на элементарные области (разбиение Z). Пусть   – наибольший из диаметров элементарных областей. Если независимо от разбиения Z существует , то он и называется площадью данной поверхности. Пусть S однозначно проектируется на плоскость xy и  G – это проекция. Элементу площади dxdy области G на плоскости xy соответствует элемент площади поверхности S, равный , где – угол между нормалью к поверхности S и осью Z. Поэтому вычисление площади поверхности сводится к вычислению двойного интеграла  по проекции поверхности на плоскость. Если поверхность задана уравнением , , а нормаль представляет собой градиент функции, то есть: , то    и площадь поверхности вычисляется по формуле:

, здесь G – проекция поверхности S на плоскость xy.

Если поверхность однозначно проектируется на другие координатные плоскости, то соответственно изменится формула вычисления площади поверхности.

Если кривая задана параметрическими уравнениями и , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми и и отрезком [a,b] оси Ox, выражается формулой где определяются из уравнений

Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением и двумя полярными радиусами  находится по формуле .

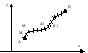
31. Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление.

Определение криволинейного интеграла первого рода, его основные свойства и вычисление.

Кривая должна быть простой кривой, то есть .

Пусть кривая будет разбита точками разбиения. Составим интегральную сумму.

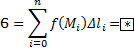
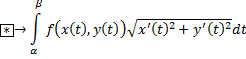
Полученный интеграл называется криволинейным интегралом первого рода.

На словах можно сказать так. Если существует предел интегральной суммы (см. выше) при стремлении к нулю наибольшей из длин Δlk (то есть ), то этот предел называется криволинейным интегралом первого рода от функции f(x,y) по кривой L и обозначается символом или .

Если кривая задана не параметрически, а, к примеру, так: , тогда .

Основные свойства:

Линейность:

Аддитивность (если дуга AB составлена из двух дуг AC и CB):

Монотонность: если f<=g на L, то:

Изменение направления обхода кривой интегрирования не влияет на знак:

Оценка модуля интеграла:

Вычисление. Пусть L – кривая, как на рисунке, заданная параметрически. Пусть функция f(x,y) определена и интегрируема вдоль кривой l как криволинейный интеграл первого рода. Тогда: .

Таким образом, для вычисления по длине дуги АВ надо, используя параметрическое уравнение кривой, выразить подынтегральную функцию через параметр t, заменить dl дифференциалом дуги в зависимости от параметра t и проинтегрировать полученное выражение по t.

Определение криволинейного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.

П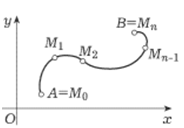усть кривая L на координатной плоскости Оху задана параметрически уравнениями. L называется простой (плоской) незамкнутой кривой, если функции, непрерывны на и различным значениям параметра t из сегмента соответствуют различные точки,. Если точка совпадает с точкой , а остальные точки не являются кратными, то L называется простой замкнутой кривой. Простая кривая L называется спрямляемой, если существует предел (длинa кривой L) длин ломаных, вписанных в кривую, при Δt → 0.

Пусть на кривой AB заданы две функции, P(x, y) и Q(x, y). Разобьем сегмент на n частей точками . Кривая АВ разобьется на n частей точками в направлении от A к B. Пусть – координаты точки ,,, – длина дуги . На каждой дуге возьмем некоторую точку (координаты ) и составим две интегральные су­ммы: , . Если существует предел интегральной суммы при стремлении к нулю наибольшей из длин , то этот предел называется криволинейным интегралом второго рода . Сумма называется общим криволинейным интегралом второго рода.

Из определения криволинейного интеграла второго рода следует, что при изменении направления обхода кривой AB изменяется и знак интеграла . Аналогично вводится для пространственной кривой, заданной параметрически

Криволинейные интегралы обладают теми же свойствами, что и обычные определенные: Линейность . Аддитивность: . Монотонность: если f≤g, то .

Кривая L кусочно-гладкая, если она непрерывна и распадается на конечное число не имеющих общих внутренних точек кусков, каждый из которых представляет собой гладкую кривую.

Вычисление криволинейного интеграла второго рода с помощью определенного интеграла.

Если AB – кусочно-гладкая кривая, а функции Р=Р(x,y) и Q=Q(x,y) кусочно непрерывны вдоль кривой AB, то справедливо равенство: =.

Если кривая AB задана уравнением y = у(x), a≤x≤b, и имеет кусочно-непрерывную производную, а функции P(x,y) и Q(x,y) кусочно непрерывны вдоль кривой AB, то имеет место равенство:=.

Связь между криволинейными интегралами первого и второго рода.

Пусть AB− кусочно гладкая кривая, функции Р=P(x,y) и Q=Q(x,y) кусочно непрерывны вдоль кривой AB и − единичный касательный вектор к кривой AB в точке M(x,y), причем направление соответствует направлению движения от А к В (α − угол между векторомв точке M(x, y) и осью Oх).. Для пространственной кривой справедлива аналогичная теорема:.

Из лекций:

Это и есть криволинейный интеграл второго рода.

– то же самое, только по y.

Каждый интеграл второго рода может быть сведён к первому роду.

или

32+нет доказательства!. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.

Ф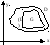ормула Грина: Если C – замкнутая граница области D и функции P(x,y) и Q(x,y) вместе со своими частными производными первого порядка непрерывны в замкнутой области D (включая границу C), то справедлива формула Грина: , причем обход вокруг контура C выбирается так, что область D остается слева.

Из лекций (не МВД2015): Пусть заданы функции P(x,y) и Q(x,y), которые непрерывны в области D вместе с частными производными первого порядка. Интеграл по границе (L), целиком лежащий в области D и содержащий все точки в области D: . Положительное направление контура такое, когда ограниченная часть контура находится слева.

У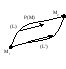словие независимости криволинейного интеграла 2-го рода от пути интегрирования. Необходимым и достаточным условием того, что криволинейный интеграл первого рода, соединяющий точкиM₁ и M₂, не зависит от пути интегрирования, а зависит только от начальной и конечной точек, является равенство: .

.

.

.