9. Вычисление определенного интеграла по частям и заменой переменной.

При выводе формулы интегрирования по частям было получено равенство u dv =d (uv) –v du. (d (uv)= u dv+ v du)

Проинтегрировав его в пределах от aдоbи учитывая теорему «о свойствах определённого интеграла», получим

Как это следует из теоремы «о свойствах неопределённого интеграла», первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. Записав эту разность кратко в виде

получаем формулу интегрирования по частям для вычисления определенного интеграла:

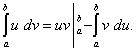
Перейдём к вычислению определённого интеграла методом замены переменной.

Пусть

где, по определению, F(x) – первообразная для f(x). Если в подынтегральном выражении произвести замену переменной

то в соответствии с формулой (16?) можно записать

В этом выражении

первообразная функция для

В самом деле, её производная, согласно правилу дифференцирования сложной функции, равна

Пусть α и β – значения переменной t , при которых функция

принимает соответственно значения aи b, т.е.

Тогда

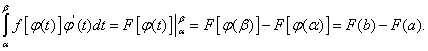
Но, согласно формуле Ньютона-Лейбница, разность F(b) – F(a) есть

поскольку F(x) – первообразная для f(x).

Итак,

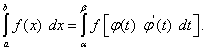(50)

Это и есть формула перехода к новой переменной под знаком определённого интеграла. С её помощью определённый интеграл

после замены переменной преобразуется в определённый интеграл относительно новой переменной t. При этом старые пределы интегрированияa и b заменяются новыми пределами α и β. Чтобы найти новые пределы, нужно в уравнение

поставить значения x = a и x = b, т.е. решить уравнения

и

относительно α и β. После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.

При вычислении определённого интеграла методом замены переменной часто бывает удобно выражать не старую переменную как функцию новой, а, наоборот, новую – как функцию старой.

10. Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения).

Вычисление площадей плоских фигур:

Прямоугольные координаты

Площадь криволинейной трапеции, расположенной «выше» оси абсцисс (ƒ(х) ≥ 0), равна соответствующему определенному интегралу:

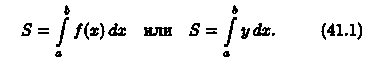
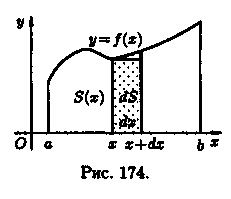
Формула (41.1) получена путем применения метода сумм. Пусть криволинейная трапеция ограничена линиями у = ƒ(х) ≥ 0, х = а, х = b, у = 0 (см.  рис. 174).

Для нахождения площади S этой трапеции проделаем следующие операции:

1. Возьмем произвольное х  [а; b] и будем считать, что S = S(x).

2. Дадим аргументу х приращение Δх = dx (х + Δх є [а; b]). Функция S = S(x) получит приращение ΔS, представляющее собой площадь «элементарной криволинейной трапеции» (на рисунке она выделена).

Дифференциал площади dS есть главная часть приращения ΔS при Δх → 0, и, очевидно, он равен площади прямоугольника с основанием dx и высотой у: dS = у • dx.

3. Интегрируя полученное равенство в пределах от х = а до х = b, получаем

О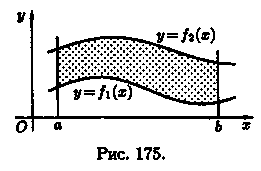тметим,что если криволинейная трапеция расположена «ниже» оси Ох (ƒ(х) < 0), то ее площадь может быть найдена по формуле

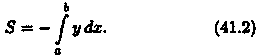
Формулы (41.1)и (41.2) можно объединить в одну:

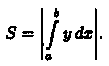
Если криволинейная трапеция ограничена прямыми у = с и у=d, осью Оу и непрерывной кривой х = φ(у) ≥ 0 (см. рис. 177), то ее площадь находится по формуле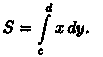

И, наконец, если криволинейная трапеция ограничена кривой, заданной параметрически

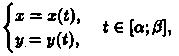
прямыми х = а и х = b и осью Ох, то площадь ее находится по формуле

где а и β определяются из равенств х(а) = а и х(β) =b.

Полярные координаты

Найдем площадь S криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией r=r(φ) и двумя лучами φ=а и φ=β (а < β), где r и φ — полярные координаты (см. рис. 180).

1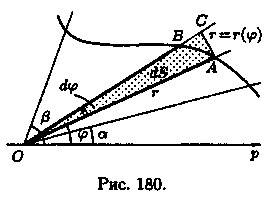. Будем считать часть искомой площади S как функцию угла φ, т. е. S = S(φ), где а ≤φ≤β (если φ = а, то S(a) = 0, если φ=β, то S(β) = S).

2. Если текущий полярный угол φ получит приращение Δφ = dφ, то приращение площади AS равно площади «элементарного криволинейного сектора» OAB.

Дифференциал dS представляет собой главную часть приращения ΔS при dφ→0 и равен площади кругового сектора О АС (на рисунке она  заштрихована) радиуса r с центральным углом dφ. Поэтому

3. Интегрируя полученное равенство в пределах от φ = а до φ = β, получим искомую площадь

Вычисление длины дуги плоской кривой

Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.

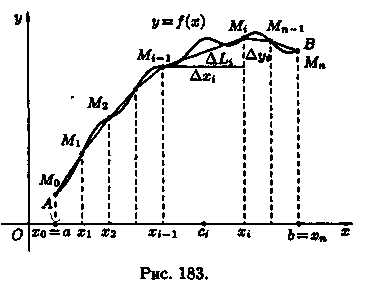
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у' = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную

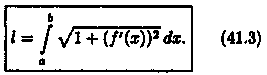
1. Точками х₀ = а, х₁..., х_n = b (х₀ < x₁ < ...< х_n) разобьем отрезок [а; b] на n частей (см. рис. 183).  Пусть этим точкам соответствуют точки М₀ = А, M₁,...,M_n =В на кривой АВ. Проведем хорды М₀M₁, M₁M₂,..., М_n-1М_n, длины которых обозначим соответственно через ΔL₁, AL₂,..., ΔL_n. Получим ломаную M₀M₁M₂ ... M_n-ιM_n, длина которой равна L_n=ΔL₁ + ΔL₂+...+ ΔL_n =

2. Длину хорды (или звена ломаной) ΔL₁ можно найти по теореме Пифагора из треугольника с катетами Δx_i и Δу_i:

По теореме Лагранжа о конечном приращении функции Δу_i=ƒ'(с_i)•Δх_i, где ci є (x_i-1;x_i). Поэтому

а длина всей ломаной M₀M₁... М_n равна

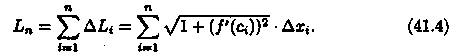
3.Длина l кривой АВ, по определению, равна

.

Заметим, что при ΔL_i→0 также и Δx_i →0 ΔLi =и, следовательно, |Δx_i|<ΔL_i).

Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δx_i→ 0:

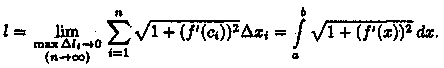
Таким образом,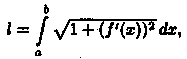или в сокращенной записи  l =

Вычисление объема тела

Вычисление объема тела по известным площадям параллельных сечений

Пусть требуется найти объем V тела, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ох: S = S(x), а ≤ х ≤ b.

1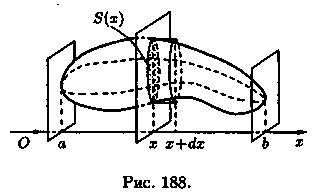. Через произвольную точку х є [a;b] проведем плоскость ∏, перпендикулярную оси Ох (см. рис. 188). Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении х. Через v(x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; х] величина v есть функция от х, т. е. v = v(x)  (v(a) = 0, v(b) = V).

2. Находим дифференциал dV функции v = v(x). Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках х и х+Δх, который приближенно может быть принят за цилиндр с основанием S(x) и высотой dx. Поэтому дифференциал объема dV = S(x) dx.

3. Находим искомую величину V путем интегрирования dV в пределах от а до b:

Полученная формула называется формулой объема тела по площади параллельных сечений.

 Объем тела вращения

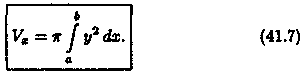
Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = ƒ(х), отрезком а ≤ x ≤ b и прямыми х = а и х = b (см. рис. 190). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох (хÎ [а; b]), есть круг с радиусом у = ƒ(х). Следовательно, S(x)=πy^2.

П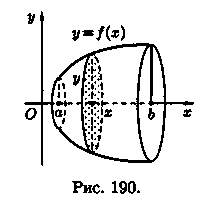рименяя формулу (41.6) объема тела по площади параллельных сечений, получаем

Если криволинейная трапеция ограничена графиком не прерывной функции х=φ(у) ≥ 0 и прямыми х = 0, у = с,

у = d (с < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой (41.7), равен

11++. Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости.

Выражение(1)

где (u_k)kÎ N — заданная числовая последовательность, называется числовым рядом. Конечные суммы S₁ = u₁, S₂ = u₁ + u₂, .... S_n = u₁ + u₂ +...+ u_n, называются частичными суммами ряда (1).

Если существует конечный предел последовательности частичных сумм (2)

то ряд (1) называется сходящимся, а число S—суммой ряда (1)

Необходимое условие сходимости:

Если ряд (1) сходится, то

Доказательство:

Пусть ряд u₁+u₂+…+u_n… сходится, то есть существует конечный предел =S. Тогда имеет место также равенство=S, так как при nи (n-1). Вычитая почленно из первого равенства второе, получаем-==u_n=0, что и требовалось доказать.

Критерий Коши:

Для того чтобы числовой ряд (1) был сходящимся, необходимо и достаточно, чтобы для любого ε > 0 су­ществовало N = N(ε) такое, что для всех n > N и р = 1, 2, … выполнялось неравенство:

Доказательство:

=>

Частный случай:

При p=1: |x_n+1| < ε, следовательно, (необходимое условие сходимости ряда).

12+. Признаки Даламбера и Коши сходимости рядов с неотрицательными членами.

Признак Даламбера:

Пусть дан знакоположительный числовой ряд

(7)

и пусть существует предел При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.

(Михайлов доказывал другую форму признака Даламбера, не предельную, а для , где 0<q<1 и для >1, представляя это как геом. Прогрессию. Аналогично и для признака Коши. Но доказательство практически такое же для обоих признаков – все сводится к геом. прогрессии.)

Доказательство:

По условию существует предел . Это означает, что для любого положительного числа ε существует такой номер N(ε), что для всех номеров n>N выполняется условие

или p-E<(10) (E – это ε)

Пусть сначала p<1. Выберем ε так, что p+ε=q<1. Для всех n>N имеем … или

или

(11)

Рассмотрим ряды:

(12)

. (13)

Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.

Пусть теперь p>1. Выберем ε так, что p-ε>1. Тогда из левой части неравенства (10) следует, что при n>N выполняется или u_n+1>u_n, то есть члены ряда возрастают с возрастанием номера n. Поэтому u_n≠0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.

 

Замечания:

1. Если расходимость ряда установлена с помощью признака Даламбера, то u_n≠0.

2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.

3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.

Признак Коши:

Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)

и пусть существует предел При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.

Доказательство:

По условию существует Это означает, что для любого положительного числа Е существует такой номер N, что для всех n>N выполняется условие || <E или

p-E<<p+E. (14)

Пусть p<1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем <q или u_n<qⁿ для всех n>N. Рассмотрим ряды

(15)

(16)

Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что u_n<qⁿ для всех n>N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).

Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие p-E >1. Тогда из (14) получаем >1 или u_n>1, следовательно, u_n≠0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.