13. Интегральный признак Коши сходимости числового ряда.
Пусть члены
знакоположительного числового ряда
u1+u2+…+un…
(7) не возрастают: u1≥u2≥…≥un≥…
и пусть f(x) такая положительная,
непрерывная, невозрастающая на промежутке
[1;∞) функция, что f(1)=u1,
f(2)= u2
,…, f(n)= =un,…
. Тогда ряд (7) сходится или расходится
одновременно с несобственным интегралом
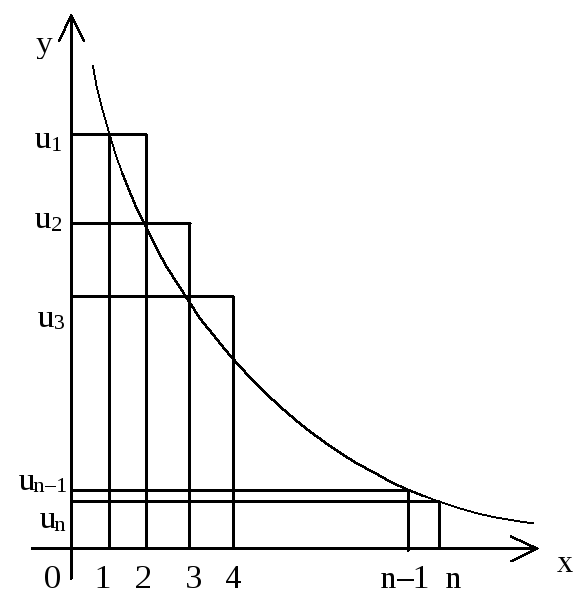
Доказательство:
Построим график функции y=f(x) на отрезке [1;n] и построим прямоугольники с основаниями [1;2], [2;3], …, [n-1;n] и высотами u1,u2,…,un-1, а также с высотами u2,u3,…,un.
Sn=u1+u2+…+un-1+un,
Sвпис=u2∙1+u3∙1+…+un∙1 = u2+u3+…+un = Sn-u1, (u1 нет, так как ряд начинается с 1, а не с 0 и отрезка [0;1] нет)
Sопис=u1∙1+u2∙1+…+ +un-1∙1 = Sn-un. (так как u1 – это площадь внешнего прямоугольника с основанием [1;2] и высотой u1)
Площадь криволинейной
трапеции S=
.
Получаем
Sвпис
< S
< Sопис
Sn-u1
<
<Sn-un.
Отсюда:
Sn<u1+
(17)
и Sn>un+
(18)
=>un+
<Sn
< u1+
Пусть
сходится. Это означает, что существует
конечный предел
=Y.
Соотношение (17) принимает вид: Sn<u1+Y
при любом n. Это означает, что
последовательность частичных сумм Sn
ряда (7) ограничена и, следовательно, ряд
(7) сходится. Пусть
расходится. Это означает, что
=∞
и тогда из (18) следует, что последовательность
частичных сумм Sn
ряда (7) неограничена и, следовательно,
ряд (7) расходится. Теорема доказана.
14++. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.
Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.
Числовой ряд вида u1-u2+u3-u4+…+ +(-1)n-1un+…, где un – модуль члена ряда, называется знакочередующимся числовым рядом.
Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.
Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно.
Признак Лейбница:
Если для знакочередующегося числового ряда
(19)
Выполняются два условия:
Члены ряда убывают по модулю u1>u2>…>un>…,
то ряд (19)
сходится, причём его сумма положительна
и не превосходит первого члена ряда.
Такой ряд называется рядом Лейбница.
Доказательство:
Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n).
По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n.
С другой стороны
S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n].
Выражение в квадратных скобках
положительно и S2n>0,
поэтому S2n<u1
для любого n.
Таким образом, последовательность
частичных сумм S2n
возрастает и ограничена, следовательно,
существует конечный
S2n=S.
При этом 0<S≤u1.
Рассмотрим теперь
частичную сумму нечётного числа членов
ряда S2n+1=S2n+u2n+1.
Перейдём в последнем равенстве к пределу
при n→∞:
S2n+1=
S2n+
u2n+1=S+0=S.
Таким образом, частичные суммы как
чётного, так и нечётного числа членов
ряда имеют один и тот же предел S,
поэтому
Sn=S,
то есть данный ряд сходится. Теорема
доказана.
Замечания:
1. Теорема Лейбница справедлива и если условие un>un+1 выполняется, начиная с некоторого номера N. Другими словами - отбрасывание конечного числа членов ряда не влияет на сходимость.
2. Условие un>un+1 не является необходимым. Ряд может сходиться, если оно не выполняется. (ЧЕГО? Это условие, иначе он уже не будет рядом Лейбница и признак не будет работать! Откуда взялось это замечание???)
15++. Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального ряда.
Определение. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают:
u1(x)+u2(x)+
… + un(x)
+ … =
(1)
Где un(x) – функции переменной x, рассматриваемые на некотором промежутке, например на отрезке [a,b].
Если фиксировать
произвольное число x0
є[a,b],
получим числовой ряд:
,
если такие ряды сходятся для каждого
x0
є[a,b],
то их суммы представляют собой функцию
S(x),
называемую суммой ряда (1).
Определение. Если при x = x0 ряд (1) сходится, то x0 называется точкой сходимости ряда (1).
Определение. Множество всех значений x, при которых функциональный ряд сходится, называется областью сходимости этого ряда.
Очевидно, что в области сходимости функционального ряда его сумма является функцией от x. Будем ее обозначать S(x).
—n-ная частичная
сумма.
Ряд называется сходящимся равномерно, если последовательность Sn(x) его частичных сумм сходится равномерно.
Отличие поточечной сходимости от равномерной:
Поточечная: в каждой
точке x0:
для
.
Для другогоx0
и того же ε будет другой номер n>N(ε),
для которого |fn(x)-f(x0)|<ε.
Равномерная
сходимость:
если для
всех x0
є[a,b],
для
Свойства равномерно сходящихся рядов.
1. Сумма S(x)
равномерно сходящегося ряда
в
областиХ,
где un(x)
(n = 1, 2, 3, …) -
непрерывные функции, является непрерывной
функцией в области Х.
2. Равномерно
сходящийся ряд
,
гдеun(x)
(n = 1, 2, 3, …) -
непрерывные функции, можно почленно
интегрировать, т.е. справедливо равенство
.
(26)
3. Если ряд
,
составленный из
функций, имеющих непрерывные производные
,
сходится в областиC
и его сумма равна S(x),
а ряд из производных
сходится
в этой области равномерно, то производная
суммы ряда
равна
сумме ряда из производных:
.
(27)
Определение.
Частными (частичными) суммами
функционального ряда
называются
функции
Определение.
Функциональный ряд
называется
сходящимся в точке (х=х0),
если в этой точке сходится последовательность
его частных сумм. Предел последовательности
называется
суммой ряда
в
точке х0.
Определение.
Совокупность всех значений х, для которых
сходится ряд
называется
областью сходимости ряда.
Определение. Ряд
называется
равномерно сходящимся на отрезке[a,b],
если равномерно сходится на этом отрезке
последовательность частных сумм этого
ряда.
Теорема. (Критерий Коши равномерной сходимости ряда)
Для равномерной
сходимости ряда
необходимо
и достаточно, чтобы для любого числаε>0
существовал такой номер N(ε),
что при n>N
и любом целом p>0
неравенство |un+1(x)+un+2(x)+
… + un+p(x)|
< ε
выполнялось
бы для всех х
на отрезке [a,b].
16+. Признак Вейерштрасса равномерной сходимости.
Признак Вейерштрасса (достаточный признак равномерной сходимости ф. ряда):
Если числовой ряд
с неотрицательными членами
сходится,
и для членов функционального ряда
при всехn
и всех
выполняется
,
то ряд сходится абсолютно и равномерно
в областиX.
Говорят в этом
случае, что числовой ряд
«мажорирует» исходный функциональный
ряд, а сам числовой ряд называют
мажорантным.
Существует простой признак для проверки равномерной сходимости (принак Вейерштрасса)
Можно рассматривать 
и
при этом сохраняется терминология
числовых рядов, связанная с абсолютной
и условной сходимостью.
Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость.
Теорема (Вейерштраса):
,
, 
—
сходится. Тогда 
равномерно
сходится на 
.
Доказательство:
Применим критерий Коши:
Сопоставляя с
предыдущим неравенством, которое
верно 
,
.
Тогда, по критерию Коши, ряд равномерно
сходится.
17++. Свойства равномерно сходящихся функциональных рядов. Теорема о непрерывности суммы равномерно сходящегося ряда из непрерывных функций. Теорема о почленном интегрировании и дифференцировании ряда (без доказательства).
Общие свойства функциональных рядов
О
п р е д е л е н и е. Ряды
u1(x)+u2(x)+
… + un(x)
+ … =
,
(24)
члены которых являются функциями от х, называются функциональными. Предполагается, что все функции un(x) определены и непрерывны в одном и том же интервале, конечном или бесконечном.
Ряд (24) может сходиться для одних значений х и расходиться для других.
Значение
х = х0,
при котором
получающийся из (24)
числовой ряд
(25)
сходится, называется точкой сходимости ряда (24). Совокупность всех точек сходимости ряда называется областью сходимости ряда. Областью сходимости функционального ряда обычно бывает какой-нибудь промежуток оси Ох. Говорят, что ряд (24) сходится в этой области.
Сумму n первых членов ряда (n-ю частичную сумму) обозначают через Sn(x) , а остаток ряда обозначают через Rn(x). Функциональный ряд сходится при некотором значении х, если существует конечный предел
и
.
S(x) – сумма функционального ряда. Ее можно представить в виде S(x) = Sn(x) + Rn(x). Каждому значению х из области сходимости Х соответствует определенное значение S(x).
Равномерная сходимость ряда
О п р е д е л е н и е. Функциональный ряд (24) называется равномерно сходящимся в некоторой области Х, если для любого сколь угодно малого числа ε > 0 можно указать такое целое число N(ε) > 0, зависящее только от ε и не зависящее от х, что при всех n > N(ε) неравенство |Rn(x)| < ε выполняется для всех х из области Х.
Достаточный признак равномерной сходимости функционального ряда – признак Вейерштрасса
Если
члены функционального ряда (24) u1(x),
u2(x),u3(x),…,
un(x)…
в некоторой области Х по абсолютной
величине не превосходят соответствующих
членов некоторого сходящегося числового
ряда с положительными членами
,
то функциональный ряд
u1(x)+u2(x)+
… + un(x)
+ … =
,
в этой области сходится равномерно.
Это
значит, что во всех точках области Х
должно выполняться неравенство
,
(n = 1, 2, 3, …).
Ряд
называется
мажорантным (усиливающим) по отношению
к ряду (24).
Свойства равномерно сходящихся функциональных рядов:
1.
Сумма S(x)
равномерно сходящегося ряда
в
области Х,
где un(x)
(n
= 1, 2, 3, …) - непрерывные функции, является
непрерывной функцией в области Х.
2.
Равномерно
сходящийся ряд
,
где un(x)
(n
= 1, 2, 3, …) -непрерывные функции, можно
почленно интегрировать, т.е. справедливо
равенство
.
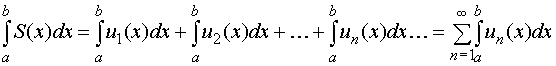(26)
3. Если ряд
u1(x)+u2(x)+
… + un(x)
+ … =
,
составленный
из функций, имеющих непрерывные
производные
,
сходится в областиC
и его сумма равна S(x),
а ряд из производных
сходится
в этой области равномерно, то производная
суммы ряда S′(x)
равна сумме ряда из производных:
S′(x)
= u′1(x)+u′2(x)+
… + u′n(x)
+ … =
(27)
Коротко эту теорему формулируют так:
Если ряд, составленный из производных сходящегося ряда (27), сходится равномерно, то исходный ряд (24) можно почленно дифференцировать.
Отметим:
здесь не предполагаются равномерная
сходимость исходного ряда, а также
дифференцируемость его суммы; они
следуют из условий теоремы. Однако
проверка равномерной сходимости ряда
является
обязательной; при невыполнении этого
теорема может потерять смысл (т.е.
оказаться неприменимой).
18+-(нет доказательства теоремы). Степенной ряд. Теорема Абеля.
Важным случаем функциональных рядов являются степенные ряды:
(13)
или
Для выяснения
свойств степенных рядов достаточно
ограничиться рассмотрением рядов вида
(13), так как ряд по степеням
легко свести к виду (13) заменой переменных
,
т.е. переносом начала координат в точку
Для выяснения характера области сходимости степенного ряда сформулируем следующую теорему:
Теорема 6.1. (Абеля):
Пусть степенной
ряд (13) сходится в точке
Тогда он сходится абсолютно для всех
х, таких, что
и равномерно в любой области
Следствие: Если
степенной ряд (13) расходится в точке
x1,
то он расходится и во всех точках x
таких, что
.
Для определения области сходимости степенного ряда используется либо признак Даламбера, либо признак Коши.
Рассмотрим степенной ряд:
.
(14)
Вычислим предел:
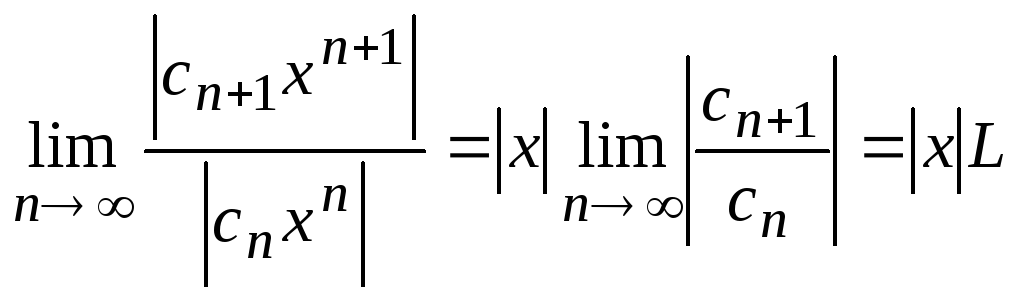.(15)
Если существует
предел (15), то ряд (14) сходится, если
,
и расходится, если
.
Следовательно, ряд (14) сходится
абсолютно, если
,
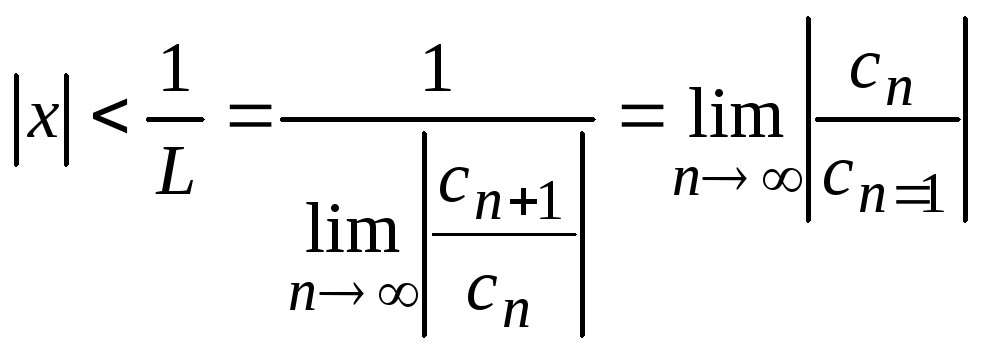и расходится, если
.
Определение:
Число
,
такое, что для всех x, удовлетворяющих
условию
ряд (13) сходится, а для всех х
удовлетворяющих условию
ряд расходится, называется радиусом
сходимости ряда.
Формула для радиуса сходимости, получаемая с помощью признака Даламбера, имеет вид
(16)
Область сходимости ряда - так называют множество точек сходимости функционального ряда, т.е. множество значений аргумента х, для которых ряд (бесконечная сумма) сходится
Пример 6.1.
Найти область сходимости ряда Область сходимости ряда
при
.
По признаку Даламбера:
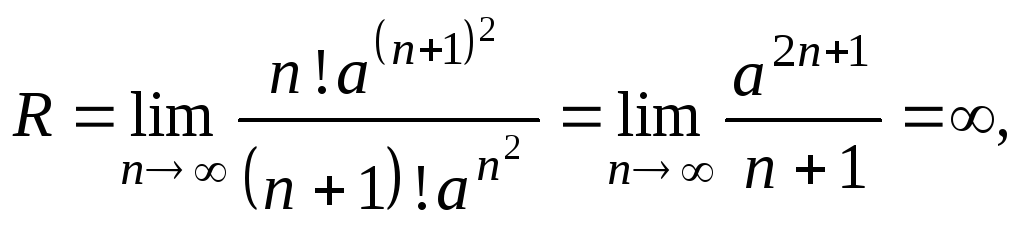
что означает, что ряд сходится на всей оси Х.
19++. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.
Из т. Абеля следует, что степенной ряд сходится в области |x-x0| < R, которая называется радиусом сходимости.
Найдем этот радиус.
Применим признак Коши сходимости числового ряда:
=>
ряд сходится,
un
= an(
x
- x0)n
=>
,
,
тогда ряд сходится в области
Следовательно, радиус сходимости степенного ряда определяется формулой:
(формула
Коши – Адамара)
Итак, в своей области
сходимости степенной ряд сходится к
некоторой функции f(x),
т.е.
20+. Вопрос для консультации – надо ли доказывать? На лекциях Михайлов не доказывал!
Кроме того – лучше его переспросить еще раз и саму теорему, так как в его интерпретации она отличается от общепринятой формулировки, в которой требуется только лишь существование всех производных, а вовсе не их ограниченность ≤n!!!
Ряд Тейлора. Теорема Тейлора о разложимости функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора-Маклорена: ex,sinx,cosx, (1+x)a,ln(1+x).
(Формулировка с лекции Михайлова от 26.03.15 будет ниже).
Пусть функция
бесконечно
дифференцируема в некоторой окрестности
точки
.
Формальный ряд
называется рядом
Тейлора функции
в
точке
.
В случае, если
,
этот ряд также называется рядом Маклорена.
Пусть 
.
Тогда ряд
называется
рядом Тейлора функции
в
точке
.
Если 
,
то
по
формуле Тейлора:
, где 
-
остаточный член формулы Тейлора, т.е.
,
где
-
n-ая частичная сумма ряда Тейлора
функции
в
точке
ряд
Тейлора сходится на
тогда
и только тогда, когда
Пусть 
и
,
тогда на
Доказательство:
,
где 
-
остаточный член формулы Тейлора в форме
Лагранжа:
.
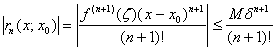Рассмотрим
ряд 
,
по
признаку Даламбера ряд сходится
.
Перейдем к пределу при
в
неравенстве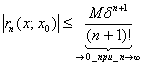
на
.
Теорема Тейлора
Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.{Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.
Пусть х - любое
значение из этой окрестности, но а
х
Тогда между точками х и а найдется
такая точка ,
что справедлива формула:
это
выражение называется формулой Тейлора,
а выражение:
называется
остаточным членом в форме Лагранжа.
Михайлов формулировал без остаточного члена, и, соответственно, не использовал ε, у него не было остатка и разложение было бесконечным, а не до n . Зато у него было дополнительное условие, его формулировка (26.03.15):
Если в некоторой
окрестности точки x0
= a
производные всех порядков функции f(x)
равномерно ограничены, т.е. |f(k)(x)|
≤ n
для всех k,
то f(x)
представима, и при том единственным
образом, степенным рядом:
Доказательство.
Представим функцию f(x)
в виде некоторого многочлена Pn(x),
значение которого в точке х
= а равно
значению функции f(x),
а значения его производных равно
значениям соответствующих производных
функции в точке х = а.
(1)
Многочлен
Pn(x)
будет близок к функции f(x).
Чем больше значение n,
тем ближе значения многочлена к значениям
функции, тем точнее он повторяет
функцию.
Представим этот многочлен
с неопределенными пока коэффициентами:
(2)
Для
нахождения неопределенных коэффициентов
вычисляем производные многочлена в
точке х = а и составляем систему
уравнений:
(3)
Решение
этой системы при х = а не вызывает
затруднений, получаем:
…………………….
Подставляя
полученные значения Ci
в формулу (2), получаем:
Как
было замечено выше, многочлен не точно
совпадает с функцией f(x), т.е. отличается
от нее на некоторую величину. Обозначим
эту величинуRn+1(x).
Тогда: f(x) =
Pn(x)
+ Rn+1(x)
Теорема
доказана.
для
всех
для всех
для всех
и всех
комплексных α где
21++. Ряд Фурье. Разложение функций: в общий ряд Фурье, в ряд по синусам, в ряд по косинусам.
Ряд Фурье:
,
если этот ряд сходится на некотором
промежутке, то назовем эту функциюf(x).
Обратный вопрос: представима ли рядом Фурье некоторая данная f(x)?
Вначале рассмотрим функцию на отрезке [-π;π]. Предположим, что разложение имеет место:
Чтобы получить an умножим обе части на cos(kx) и проинтегрируем:
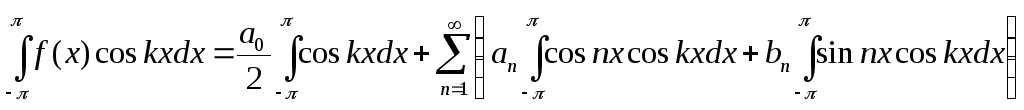
При всех n≠k интегралы равны 0:
,
а для sinnx∙cosnx
– равно 0 даже при n=k.
Получим:
Аналогично, после домножения на sin(kx):
1) При xє(-π;π) и в которых f(x) непрерывна, ряд сходится к f(x).
2) В точках разрыва
ряд Фурье сходится к
3) В точках x=±π
ряд сходится к
Если промежуток от [-L;L], то делается замена: x = π/L ∙ y:
22-. Функции многих переменных. Понятие n-мерного евклидового пространства. Множество точек евклидового пространства. Последовательность точек и ее предел. Определение функции нескольких переменных.
Выше мы говорили о функциях от одной переменной. Но можно говорить также о функциях двух, трех и вообще n переменных. Функция от двух переменных определяется следующим образом. Рассматривается множество E пар чисел (x,y). При этом имеются в виду упорядоченные пары. Это значит, что две пары (x1,y1) и (x2,y2) считаются равными (совпадающими) тогда и только тогда, когда x1=x2 и y1=y2. Если, в силу некоторого закона, каждой паре (x,y)єE приведено в соответствие число Z, то говорят, что этим определена на множестве E функция z=f(x,y) от двух переменных x и y.
Так как каждой паре чисел (x,y) соответствует на плоскости, где введена декартова система координат, точка с абсциссой x и ординатой y, и, наоборот, каждой точке, таким образом, соответствует пара (x,y), то можно говорить, что наша функция f(x,y) задана на множестве E точек плоскости.
Функцию z=f(x,y) от двух переменных изображают в трехмерном пространстве, где задана прямоугольная система координат X,Y,Z в виде геометрического места точек (x, y, f(x,y)), проекции которых (x,y) принадлежат множеству E определения f.
Например, таким геометрическим местом для функции
,
является верхняя половина шаровой поверхности радиуса 1 с центром в нулевой точке.
В этом же духе можно определить функцию трех переменных. Областью ее определения может теперь служить некоторое множество упорядоченных троек чисел (x,y,z) или, что все равно, соответствующих им точек трехмерного пространства, где введена декартова система координат.
Если каждой тройке чисел (точке трехмерного пространства) (x,y,z)єE , в силу некоторого закона, соответствует число u, то говорят, что этим на E определена функция u=F(x,y,z).
Аналогично можно рассматривать множество E упорядоченных систем (x1, … xn) из n чисел, где n - заданное натуральное число. Опять, если каждой такой системе, принадлежащей E, соответствует в силу некоторого закона число Z, то говорят, что Z есть функция от переменных x1, … xn, определенная на множестве E, и записывается эта функция в виде z=f(x1, … xn).
В случае n>3 в нашем распоряжении уже нет реального n - мерного пространства, чтобы использовать его для изображения систем (x1, … xn) в виде принадлежащих ему точек. Но математики выдумали n-мерное пространство, и оно им благополучно служит, и притом не хуже, чем реальное трехмерное пространство. Именно, n-мерным пространством называется множество всевозможных систем n чисел (x1, … xn) .
Если две функции
f и φ от
n переменных
заданы на одном и том же множестве
E систем
(x1,
… xn) -
точек n-мерного
пространства, - то можно определить
сумму f+φ,
разность f-φ,
произведение f∙φ и
частное f/φ,
как функции, определенные на E при
помощи равенств, аналогичных равенствам
(2), где надо только числа x заменить
системами (x1,
… xn) .
Естественным образом определяются
также сложные функции, такие, как
,
где
-
тройки чисел, принадлежащих некоторому
множеству троек.
N-мерная евклидова геометрия — обобщение евклидовой геометрии на пространство большего числа измерений. Хотя физическое пространство является трёхмерным, и человеческие органы чувств рассчитаны на восприятие трёх измерений, N-мерная геометрия широко применяется в качестве математического инструмента при решении различного рода задач, связанных с манипулированием большим числом параметров (например, задачи оптимизации с большим числом переменных, задачи геометрической вероятности).
Система координат
Поскольку достаточно трудно работать с многомерными объектами, используя интуитивные представления трёхмерного мира, в N-мерной геометрии широко применяются аналитические методы. В качестве системы координат чаще всего используется прямоугольная декартова система с числом осей более трёх. Таким образом, некоторая точка А представляется в N-мерной геометрии как набор из N действительных чисел
Несмотря на то, что интуитивно трудно представить себе четыре взаимно перпендикулярные оси, понятие перпендикулярности естественным образом обобщается из трёхмерного пространства на случай четырёх и более измерений. Так, скалярное произведение взаимно перпендикулярных векторов в случае N измерений также равно нулю.
Евклидово пространство однородно и изотропно, то есть его свойства, в том числе и формула для расстояния, не зависят ни от положения начала координат, ни от направления осей координат. Это даёт возможность свободно вращать и переносить объекты, не изменяя их геометрических свойств.
В N-мерном пространстве существуют подпространства всех размерностей k<N , часто называемые гиперплоскостями или k-плоскостями, где k — размерность подпространства. Термин «гиперплоскость» используется также в узком смысле для обозначения подпространства размерности N–1 (коразмерности 1). Одномерное подпространство по аналогии с обычной геометрией называется прямой, двумерное подпространство — плоскостью. Никакого принципиального различия между k-плоскостью и k-пространством нет. Название «плоскость» подчёркивает тот факт, что объект находится внутри пространства большей размерности, то есть является подпространством. Например, в 4-пространстве обычное трёхмерное пространство является 3-плоскостью.
Можно показать, что в пространстве размерности N имеет место аналогичная ситуация — подпространство размерности k задаётся системой N–k линейных уравнений:
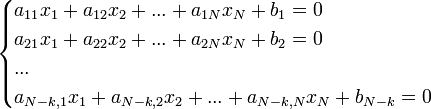
Если каждой
упорядоченной паре чисел
по
некоторому закону
поставлено
в соответствие единственное действительное
число
,
то говорят, что задана функция двух
переменных
или
.
Числа
называются
при этом независимыми переменными или
аргументами функции, а число
–
зависимой переменной.
23-. Предел функции нескольких переменных. Непрерывность функции. Частные производные.
Определение. Число
А
называется пределом функции f(M),
где М(x1,x2,…xn)
– точка n-мерного
пространства, при стремлении точки М
к точке М0(x10,x20,…xn0)
любым образом, если для всякого сколь
угодно малого ε>0
существует такое число δ>0,
что из условия |MM0|<δ,
где |MM0|
- расстояние между точками М и М0,
следует
<ε.
Обозначается:
А
.
Пусть z=f(x,y). Придадим
x и y приращения
и
.
Получим приращение
функции
z=f(x,y). Если
,
(1)
т.е. бесконечно малым аргументам соответствует бесконечно малое приращение функции, то говорят, что функция непрерывна.
Распишем
x0+
y+
-f(x0,y0)
и положим x0+
x=x,y0+
,то выражение(1) можно записать в виде
f(x,y)=f(x
0,y0),
(2)
т.е. непрерывность функции означает, что ее предел равен ее значению от пределов аргументов.
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области. Если в некоторой точке не выполняется условие (2), то эта точка называется точкой разрыва.
Частные производные.
Пусть z=f(x,y).
Зафиксируем какую-либо точку (x,y), а
затем, не меняя закрепленного значения
аргумента y, придадим аргументу x
приращение
.
Тогда z получит приращение, которое
называется частным приращением z по x и
обозначается
и
определяется формулой
.
Аналогично, если
x сохраняет постоянное значение, а y
получает приращение
,
то z получает частное приращение z по
y,
.
Определение. Частной
производной по x от функции z=f(x,y) называется
предел отношения частного приращения
по
x к приращению
при
стремлении
к
нулю, т.е.
Частная производная
обозначается одним из символов
.
Аналогично определяется частная производная по y:
.
Таким образом, частные производные функции двух переменных вычисляются по тем же правилам, что и производные функции одного переменного.
Пример. Найти частные производные функции z=x2e x-2y.
Решение.
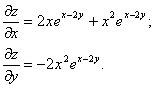
Частные производные функции любого числа переменных определяются аналогично.
4. Геометрическая интерпретация частных
производных функции двух переменных
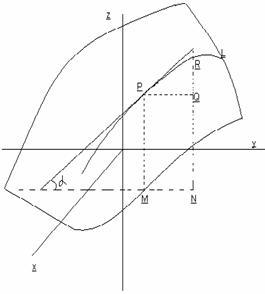
Пусть уравнение
z=f(x,y) –это уравнение поверхности.
Проведем плоскость x=const. L- линия
пересечения поверхности с плоскостью
x=const. При данном x на плоскости ХОУ возьмем
точку М. На поверхности z=f(x,y) ей
соответствует точка Р(x,y,z). Дадим
переменному y приращение
Тогда
функция z получит приращение
Отношение
равно
тангенсу угла, образованного секущей
RР с положительным направлением оси
ОУ,
Итак, частная
производная
численно
равна тангенсу угла
наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const.
Аналогично,
частная производная
численно
равна тангенсу угла наклона касательной
к кривой, получающейся в сечении
поверхности z=f(x,y) плоскостью x=const.
24+--. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.
Производные ФНП.
Рассмотрим функцию
u = F(x1,
… xn),
определенную в некоторой области D.
Пусть
− фиксированная точка. Дадим координате
х1 приращение
.
Если существует конечный предел
,
то он называется частной производной
функции F(x) по переменнойх1
и обозначается
Аналогично определяются частные производные по всем остальным переменным.
Замечания.
1. Частная производная по какой либо переменной есть обычная производная, при условии, что все остальные переменные – константы.
2. Последнее обозначение, в отличие от функций одной переменной, не равно частному от деления двух дифференциалов, а является неразрывным символом.
В частном случае двух переменных частная производная равна тангенсу наклона касательной к сечению поверхности плоскостью, перпендикулярной ко второй переменной.
Примеры.
Частные производные высших порядков.
Вычисляя частные
производные ФНП, мы снова получаем
функцию тех же переменных, от которой
можно взять частную производную, в том
числе и по другой переменной (если она,
конечно, существует):
Частные производные по одной и той же
переменной называются повторными, а
по различным переменным – смешанными.
Например:
Примеры.
Теорема 1 (О равенстве смешанных производных). Пусть функция z = f(x,y) имеет вторые частные производные в окрестности т. М0 , непрерывные в самой точке М0.
В этом случае
{Рассмотрим функции
Для
аналогично получаем:
Из равенства
следует
.
Устремив h к нулю , в силу непрерывности
производных, получаем:
}
Если u = u(x1,…,xn), то все вторые частные производные можно записать с помощью
.
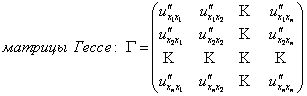Из т.1 следует, что матрица Гессе – симметрична.
Дифференциал ФНП.
Пусть функция
u = F(x)
определена в области D
и
− фиксированная точка. Дадим приращение
каждому аргументу хţ :
Величину
будем называть вектором приращения. В
свою очередь функция u получит приращение
равное
Определение 1. Функция u = F(x) называется дифференцируемой в т. х , если ее приращение может быть представлено в следующем виде:
где
Aţ = Aţ(x) и не зависит
от Δх, а
− бесконечно малая при
Величина вектора
Δх равна:
Используя это
обозначение, можно написать
Легко показать,
что
{
}
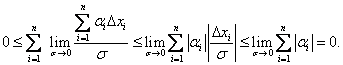Определение 2.
Главная и линейная часть приращения
дифференцируемой функции называется
дифференциалом:
Теорема 1.
Функция, дифференцируемая в т. хo −
непрерывна в этой точке. {
}
Теорема 2.
(Необходимое условие дифференцируемости)
Если F(x) дифференцируема в т. х , то она
имеет все частные производные в этой
точке, причем
{Пусть
}
Отсюда,
Если х − независимая переменная, то
и
окончательно
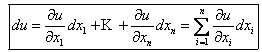
Теорема 3. (Достаточное условие дифференцируемости) Пусть F(x) имеет все частные производные в окрестности т. хо , непрерывные в самой этой точке. Тогда функция дифференцируема в т. хо .
{без доказательства}
Замечание. Для дифференцируемости функции одной переменной достаточно существования производной.
Дифференциал функции u называют полным дифференциалом.
Определение 3.
Выражение
называется дифференциальной формой.
Теорема 4.
Дифференциальная форма является полным
дифференциалом некоторой функции
u(х,у) тогда и только тогда, когда
выполнено условие
{1.Необх.:
Тогда
2. Дост. – без доказательства}
Пример. Найти общее решение дифференциального уравнения:
Геометрический смысл дифференцируемости. Касательная плоскость и нормаль к поверхности.
Рассмотрим
поверхность S: z = f(x,y), дифференцируемую
в т.
S.
Определение 1.
Плоскость, проходящая через т. М0 ,
называется касательной плоскостью к
поверхности S в т.М0 , если угол между ней
и секущей (М0М1) (
)
стремится к нулю при
.
Определение 2. Вектор, ортогональный к касательной плоскости в т.М0 , называется нормальным вектором к поверхности в этой точке. Нормалью к поверхности называется
прямая, проходящая через т.М0 перпендикулярно касательной плоскости в этой точке.
Обозначим
,
.
Вектор приращения:
Из условия
дифференцируемости функции z следует,
что
Рассмотрим
плоскость
и угол φ между секущей и этой плоскостью:
при
Отсюда
сразу следует, что плоскость П –
касательная к поверхности в т.М0. В
результате имеем:
Функция z = f(x,y),
дифференцируемая в некоторой точке
(х0,у0) имеет в соответствующей т.М0
касательную плоскость:
и нормальный вектор
Пример.
Дифференциалы высших порядков.
Определение 1.
Дифференциал от первого дифференциала
функции называется вторым дифференциалом:
Аналогично определяются дифференциалы
более старших порядков.
Вычислим второй
дифференциал функции двух переменных
.
При этом будем считать, что дифференциалы
независимых переменных dx и dy – величины
постоянные (т.е. не зависят от т.(х,у) и
не меняются при вычислении каждого
последующего дифференциала).
.
Не трудно видеть, что второй дифференциал представляет собой квадратичную форму от
переменных dx и dy. Матрица этой квадратичной формы есть матрица Гессе, т.е.
d2z = (dx,dy)Г(dx,dy)T (см. раздел «Линейная алгебра», квадратичные формы). Кроме того,
второй дифференциал
можно записать в символическом виде:
Можно показать,
что в общем случае дифференциал 2 – го
порядка функции u = F(x) равен
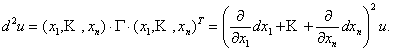
Дифференциал m –
го порядка равен
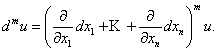
25++?-по Тейлору, у меня нет этой лекции. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.
Как известно, функцию F(T) при условии существования ее производных по порядок N+1 можно разложить по формуле Тейлора с остаточным членом в форме Лагранжа. Запишем эту формулу в дифференциальной форме:
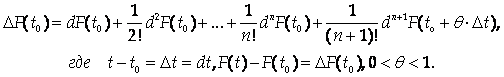
В этой форме формулу Тейлора можно распространить на случай функции нескольких переменных.
Рассмотрим функцию двух переменных F(X, Y), имеющую в окрестности точки (Х0 , у0) непрерывные производные по (N + 1)-й порядок включительно. Зададим аргументам Х И У некоторые приращения DХ и DУ и рассмотрим новую независимую переменную T:
Эти формулы задают прямолинейный отрезок, соединяющий точки (x0 ,у0) и (x0+∆x, у0+∆y). Тогда вместо приращения ∆F(x0,y0) можно рассматривать приращение вспомогательной функции
F(t) = F(x0+t ∆x, y0+t∆y),
Равное ∆F(0) = F(1) – F(0). Но F(t) является функцией одной переменной T, следовательно, к ней применима формула, приведенная в начале раздела. Получаем:
Отметим, что при Линейной замене переменных дифференциалы высших порядков обладают свойством инвариантности, то есть
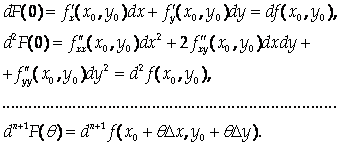
Подставив эти выражения в предыдущую формулу, получим Формулу Тейлора для функции двух переменных:
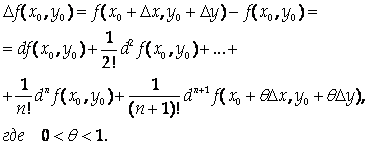
Замечание. В дифференциальной форме формула Тейлора для случая нескольких переменных выглядит достаточно просто, однако в развернутом виде она весьма громоздка. Например, даже для функции двух переменных первые ее члена выглядят так:
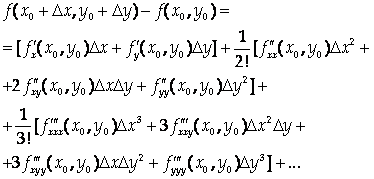
Максимум и минимум функции нескольких переменных
Напомним, что под окрестностью точки плоскости понимается внутренность любого прямоугольника, окружающего эту точку, исключая саму точку (проколотая окрестность).
В пространстве это будет произвольный параллелепипед, содержащий эту точку за вычетом самой точки.
Определение. Максимумом (строгим) функции f(x, y) называется такое значение f(x1, y1) этой функции, которое больше всех ее значений f(x, y), принимаемых данной функцией в точках некоторой окрестности точки О(х1, у1). (Окрестность может быть весьма малой по своим линейным размерам).
Определение. Минимумом (строгим) функции f(x, y) называется такое значение f(x2,y2), которое меньше всех ее значений f(x,y), принимаемых данной функцией в точках некоторой окрестности О(х2, у2).
Максимум или минимум функции f(x, y) называется экстремумом этой функции. Точка, в которой достигается экстремум, называется точкой экстремума (точка минимума, точка максимума).
Аналогично определяется экстремум функции f (x, y, z) и т.д.
Теорема. (Необходимый признак экстремума функции нескольких переменных). В точке экстремума функции нескольких переменных каждая ее частная производная первого порядка либо равна нулю, либо не существует.
Д о к а з а т е л ь
с т в о.
Пусть u = f (x, y) и f (x0,
y0)
- ее максимум (для минимума рассуждения
аналогичны). Зафиксируем одну из
переменных, например, у, полагая у =
у0,
тогда получим функцию одной переменной
U1 = f (x, yo), которая, очевидно, будет иметь
максимум при х = хо. Отсюда, на основании
теории экстремума одной переменной,
получаем, что
или
не существует.
Пусть теперь у=у0,
а х0-
фиксируем, тогда
или не существует.
С л е д с т в и е.
В точке экстремума М0
(х0,
у0)
дифференцируемой функции f
(x, y) выполнены
равенства
Для U = f(x, y, z) в
точке Мо (хо ,уо, zо) будет выполнено
условие
.
З а м е ч а н и е. Точку, в которой частные производные первого порядка либо не существуют, либо равны нулю, называют критической.
Т.е. экстремумы функции нескольких переменных могут достигаться лишь в критических точках.
Пример.
Покажем, что указанные выше условия не
являются достаточными. Пусть z = f(x,
y) = x ×
y тогда имеем
Следовательно,
Однако точка 0(0,0) не является точкой
экстремума, т.к. в любой окрестности
точки0
(о,о)
имеются точки
A (e,e) и B(- e, e) " e > 0 :
f(A) = e2 > 0 = f(0) и f(B) = -e2 < f(0).
Абсолютный экстремум
Определение. Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции. (Соответственно, абсолютный минимум, абсолютный максимум).
Теорема. (Вайерштрасс) Функция, непрерывная в ограниченной и замкнутой области, достигает в этой области своего наименьшего и своего наибольшего значения. (Без доказательства)
Теорема . Абсолютный экстремум функции в данной области достигается либо в критической точке функции, принадлежащей этой области, либо в граничной точке области. (Без доказательства)
Пример. Для функции z = x × y найти абсолютный экстремум в треугольной области S с вершинами О(0,0), А(1,0), В(0,2).
Определим
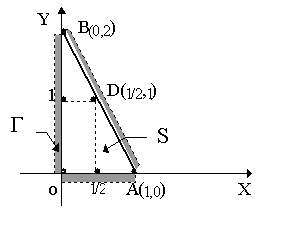
Рис. 15.1.
Критическая точка O(0,0) Î S. На участке ОА имеем у = 0 (0 £ х £ 1) и тогда z = 0.
Аналогично ОВ: х = 0 (0 £ у £ 2) Þ z = 0.
Наконец, отрезок
АВ имеет уравнение
или у = 2 - 2х (0£
х £
1).
Отсюда z = x × y = 2x - 2x2 .
Имеем
,
т.е. при
и т.к.
,
то в точке
функция Z достигает своего наибольшего
значения
на отрезке АВ.
Итак, наименьшее
значение z в S есть m=0 и оно реализуется
в точках отрезков ОВ и ОА, составляющих
часть границы Г.
достигает в точке
Теорема.
(достаточное условие экстремума)
Если
дважды
дифференцируема в стационарной точке
,
то
--
точка минимума (максимума), если
квадратичная форма
положительно
(отрицательно) определена. Если эта
форма не определена, то экстремума в
этой точке нет. Если она вырождена, то
неизвестно, является ли
точкой
экстремума.
Доказательство.
По формуле Тейлора приращение функции
в точке
можно
записать в виде
,
поскольку, по необходимому условию
экстремума, частные производные будут
равны нулю. Перепишем выражение в виде
,
причем
при
.
Заметим, что новые переменные
изменяются
на единичной сфере, т.к.
.
Кроме того, квадратичная форма
непрерывна
и по теореме Вейерштрасса на сфере
принимает наименьшее значение, обозначим
его
.
Пусть форма положительно определена.
Тогда
.
Теперь благодаря тому, что
при
можно
подобрать такое
,
что при
выполнено
,
тогда выполнено
в
этой окрестности. Что и означает, что
--
точка минимума. Для точки максимума
доказательство аналогично.
Замечание .
В случае двух переменных матрица
квадратичной формы имеет вид
.
Тогда если
,
то для положительной определенности
достаточно
--
тогда имеется минимум. Если же
,
то достигается максимум. Если же
,
то ничего сказать нельзя.
Лекция Михайлова от 16.04.15:
Точка M0(x0,y0) называется точкой максимума, если в некоторой окрестности этой точки f(x0,y0)≥f(x.y).
(Если f(x0,y0)>f(x.y), то строгий максимум.)
Точка M0(x0,y0) называется точкой минимума, если в некоторой области этой точки f(x0,y0)≤f(x.y). Строгий минимум при строгом <.
Необходимое условие экстремума дифференцируемой функции: ∂f|M=M0=0, т.е. все частные производные в точке экстремума (M0) равны нулю.
Достаточное условие экстремума:
- приращение, через
ф-лу Тейлора
Если df|M=M0=0, то точка M0 называется точкой возможного экстремума при этом приращении функции
∆f=f(x,y) – f(x0,y0) < 0 – максимум
∆f > 0 – минимум.
Т.е. наличие и характер экстремума в М0 определяется знаком второго дифференциала.
Знак второго дифференциала, а следовательно и приращения функции ∆f определяется знаком квадратного трехчлена:
,
а именно, если A>0
и D=B2-AC<0
– минимум, если A<0
и D<0
– минимум. Если D≥0
– экстремума нет.
26+. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
О
пределение
двойного интеграла. Пусть на плоскости
XY задана функцияz=f(x,y)
и область (P) (область задания функции
f(x,y)),
её площадь P. Произведём разбиение
площади сеткой кривых Pi,
где Pi
– частичная область. Внутри частичной
области возьмём произвольную точку с
координатами (ξi,ηi).
Составим интегральную сумму: 
.
Пусть λ – характеристика разбиения,
которая равна 
,
где di
– диаметр частичной области. Диаметр
– максимальное расстояние между любой
парой точек в области. Устремим λ к нулю.
Если существует предел интегральных
сумм 
,
то этот предел и называется двойным
интегралом: 
.
Основные свойства двойного интеграла:
Свойство аддитивности:
Свойства линейности:
а) 
б) 
Модуль интеграла меньше или равен интегралу от модуля:
Теорема о среднем.
Так как 
то, проинтегрировав это неравенство,
получим:
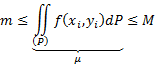
Где 
Сведение двойного интеграла к повторному.
Т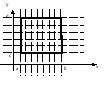
еорема.
Если функция f(x,
y) интегрируема
в прямоугольнике, указанном на рисунке,
и если 
и существует интеграл 
,
тогда существует повторный интеграл
и
он равен двойному: 
=
.
З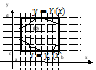
амечание.
Еслиf(x, y)
интегрируема в прямоугольнике, указанном
на рисунке, и 
и существует интеграл 
тогда
существует повторный интеграл 
.
Предположим, что
область D произвольного вида. Делаем
разбиение и проводим параллельные
линии. Заключим область (D) в прямоугольник
(D*), 
,
и в нём определим функцию f*(x,y): 
.
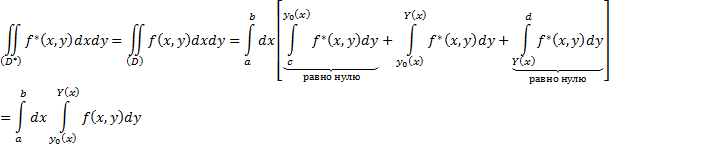
Формула в общем
виде: 
.
Так же доказывается, что 
27+. Тройной интеграл, сведение его к повторному.
О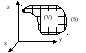
пределение
тройного интеграла. Пусть в некоторой
трехмерной области (V)
с границей (S)
задана в каждой точке функция f(x,y,z).
Разобьём тело (V)
сеткой поверхностей на частичные области
(Vi).
В каждой (Vi)
возьмём произвольную точку (ξi,
ηi,
ζi)
и составим интегральную сумму: 
.
Устремим максимальный диаметр (макс.
расстояние между любой парой точек в
области) к нулю: 
,
а количество разбиений к бесконечности:
n→∞.
Тогда, если существует предел интегральных
сумм, то он равен тройному интегралу:
.
(в пределе выше надо еще указать, что n→∞)
На всякий случай
определение интегральной суммы. Пусть
на нек-ом отрезке 
задана 
.
Произведём разбиение отрезка: 
.
Число 
,
называется интегральной суммой функции
f(x),
соответствующей данному разбиению
T(ξi;xi)
сегмента [a;b]
и данному выбору промежуточных точек
ξi
на частичных
сегментах [xi-1;xi],
Δ –хар-тика разбиения: 
С
ведение
к повторному интегралу. Рассмотрим
первый простейший случай. Пусть тело V
– прямоугольный параллелепипед. Проведём
секущую плоскость. Возьмём приращение
плоскости (жирные линии). Тогда:
.
Р
ассмотрим
второй случай.
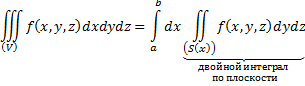
Р
ассмотрим
третий случай – область (V) цилиндрического
типа.
