- •Оглавление
- •1*. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.
- •2**. Ограниченность интегрируемой функции.
- •3**(-). Критерий интегрируемости ограниченной на отрезке функции.
- •4≠. Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций.
- •5*. Основные свойства определенного интеграла.
- •6*. Формула среднего значения для определенного интеграла.
- •7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.
- •8. Формула Ньютона-Лейбница для определенного интеграла.
- •9. Вычисление определенного интеграла по частям и заменой переменной.
- •10. Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения).
- •13. Интегральный признак Коши сходимости числового ряда.
- •28. Замена переменных в двойном интеграле. Пример: случай полярных координат.
- •29. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.
- •30. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.
- •31. Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление.
- •33. Поверхностные интегралы первого и второго рода, их основные свойства и вычисление.
- •34. Теорема Гаусса-Остроградского, ее запись в координатной и векторной (инвариантной) формах.
- •35. Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.
- •36. Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.
- •37. Оператор Гамильтона. (набла) его применение (примеры).
- •38. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (оду) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.
- •43. Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (фср) однородного уравнения, общее решение неоднородного уравнения.
- •44. Система линейных дифференциальных уравнений первого порядка. Фср однородной системы. Общее решение однородной системы.
4≠. Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций.
Следствие №3 (из критерия Коши) :
Если f(x) ограничена и монотонна на [a, b], то она интегрируема на этом отрезке.
Доказательство:
![]()
![]() ;
; ![]()
![]()
в силу монотонности функции все разности под знаком модуля в получившейся сумме имеют один знак
![]() {т.к.
{т.к. ![]() и
и ![]() }=
}=![]() ч.т.д.
ч.т.д.
Следствие №2 (из критерия Коши) :
Если функция f непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Доказательство:
f - непрерывна на
[a, b] ![]() она
равномерно непрерывна
она
равномерно непрерывна ![]()
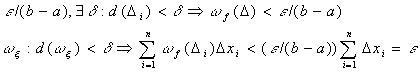 ч.т.д.
ч.т.д.
5*. Основные свойства определенного интеграла.
Основные свойства определённого интеграла. (приведены в порядке и составе М.В.Д., так что в дальнейших доказательствах ссылки в формулах не соответствуют порядку данных свойств)
![]()
1)
![]() -
не зависит от названия переменной
-
не зависит от названия переменной
2)
![]()
3)
![]() ;
;
4)
![]()
5)
![]() ;
(следует из определения интеграла как
предела интегральных сумм).
;
(следует из определения интеграла как
предела интегральных сумм).
6) Если f(x) и g(x) интегрируемы на [a,b], то f(x)∙g(x) интегрируемы на [a,b]
7) Если [a,b] разбить точкой C на два интервала: [a,c] и [c,b], то:
- Из интегрируемости f(x) на [a,b] => интегрируемость f(x) на [a,c] и [c,b],
- Из интегрируемости f(x) на [a,c] и [c,b] => интегрируемость f(x) на [a,b],
-
![]()
8) Если f(x)
интегрируема
на [a,b]
и для
![]() ,
то
,
то![]()
- Следствие 1: Если
для любого х из [a,b]
f(x)≥0
и f(x)
– интегрируема на [a,b]
=>
![]() ≥
0
≥
0
- Следствие 2: Если
f(x)
и g(x)
интегрируемы на [a,b]
и для любого х из [a,b]
f(x)
≥ g(x)
=>
![]() ≥
≥![]()
9) Если f(x)
интегрируема
на [a,b],
то |f(x)|
интегрируема на [a,b]
и
![]() ;
;
(Михайлов не называл свойства линейностью и аддитивностью и доказывал несколько иначе и не всегда то , но и так сойдет)
Линейность.
Если функции f(x),
g(x)
интегрируемы по отрезку [a,b]
, то по этому отрезку интегрируема их
линейная комбинация A
f(x)
+ B
g(x)
(A,
B
= const), и
![]()
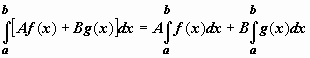 (лучше
безA
и B,
чтобы соответствовало одному их свойств
выше, но можно и так, просто тогда это
будет доказательством сразу двух свойств
по М.В.Д. – 4 и 5).
Док-во:
для любого разбиения отрезка и любого
выбора точек
(лучше
безA
и B,
чтобы соответствовало одному их свойств
выше, но можно и так, просто тогда это
будет доказательством сразу двух свойств
по М.В.Д. – 4 и 5).
Док-во:
для любого разбиения отрезка и любого
выбора точек
![]() выполняется
выполняется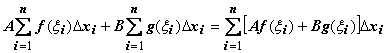
Перейдем в этом
равенстве к пределу при
![]() .
Так как существуют пределы интегральных
сумм, стоящих в левой части равенства,
то существует предел линейной комбинации
этих сумм, следовательно, существует
предел правой интегральной суммы, откуда
следует истинность и утверждения, и
равенства.
.
Так как существуют пределы интегральных
сумм, стоящих в левой части равенства,
то существует предел линейной комбинации
этих сумм, следовательно, существует
предел правой интегральной суммы, откуда
следует истинность и утверждения, и
равенства.
Аддитивность.
Если y
= f(x)
интегрируема по отрезку [a,b]
и точка c
принадлежит этому отрезку, то
![]()
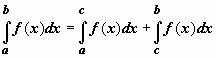 .
Док-во.
Если f(x)
удовлетворяет условиям интегрируемости
по отрезку [a,b],
то она удовлетворяет условиям
интегрируемости по отрезкам [a,c]
и [c,b].
Будем брать такие разбиения отрезка
[a,b]
, чтобы точка c
являлась одним из узлов xi:
c
= xi.
Тогда
.
Док-во.
Если f(x)
удовлетворяет условиям интегрируемости
по отрезку [a,b],
то она удовлетворяет условиям
интегрируемости по отрезкам [a,c]
и [c,b].
Будем брать такие разбиения отрезка
[a,b]
, чтобы точка c
являлась одним из узлов xi:
c
= xi.
Тогда
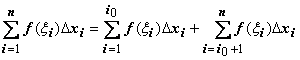 .
.
В этом равенстве
первая сумма справа - интегральная сумма
для
![]() ,
вторая - для
,
вторая - для![]() .
Переходим к пределу при
.
Переходим к пределу при![]() .
Пределы для всех трёх сумм существуют,
и
.
Пределы для всех трёх сумм существуют,
и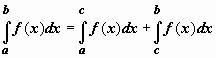 .
.
Свойство аддитивности
остаётся верным при любом расположении
точек, если только функция интегрируема
по самому широкому интервалу. Пусть,
например, c
< b
< a,
и f(x)
интегрируема по [c,
a].
Тогда, по доказанному,
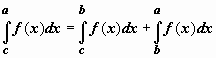 .
Отсюда и из определения интеграла для
случая, когда нижний предел больше
верхнего, следует, что
.
Отсюда и из определения интеграла для
случая, когда нижний предел больше
верхнего, следует, что![]() .
.
Интеграл от единичной функции ( f(x) = 1). Если f(x) = 1, то
 .
Док-во. Если f(x) = 1 , то для любого
разбиения
.
Док-во. Если f(x) = 1 , то для любого
разбиения
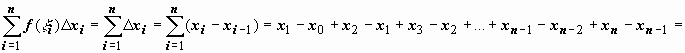 =
xn - x0 = b – a, т.е любая интегральная сумма
равна длине отрезка. Предел постоянной
равен этой постоянной, откуда и следует
доказываемое утверждение.
=
xn - x0 = b – a, т.е любая интегральная сумма
равна длине отрезка. Предел постоянной
равен этой постоянной, откуда и следует
доказываемое утверждение.
Теорема об интегрировании неравенств. (В случае М.В.Д. – это не теорема, а следствие свойства 8)
Если в любой точке
![]() выполняется
неравенство
выполняется
неравенство![]() ,
и функции f(x), g(x) интегрируемы по отрезку
[a,b], то
,
и функции f(x), g(x) интегрируемы по отрезку
[a,b], то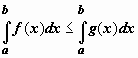 .
Док-во. Для любого разбиения отрезка
и любого выбора точек
.
Док-во. Для любого разбиения отрезка
и любого выбора точек![]() при
при![]()
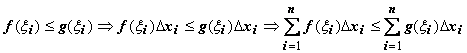 .
Переходя в этом неравенстве к пределу
при
.
Переходя в этом неравенстве к пределу
при![]() ,
получаем требуемое неравенство.
,
получаем требуемое неравенство.
Теоремы об оценке
интеграла. (а
вот и само св-во 8 по М.В.Д. – на всякий
случай лучше и не называть его теоремой,
а доказать как свойство.)
1.
Если на отрезке [a,b] функция удовлетворяет
неравенству
![]() ,
то
,
то![]()
![]()
![]()
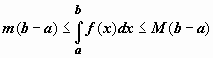 .
.![]()
![]() Док-во.
Докажем левое неравенство (цифрами над
знаками импликации обозначены номера
применяемых ранее доказанных свойств):
Док-во.
Докажем левое неравенство (цифрами над
знаками импликации обозначены номера
применяемых ранее доказанных свойств): .
.
Аналогично
доказывается и правое неравенство.
2.
Если функция f(x) интегрируема по отрезку
[a,b], то
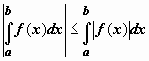 .
Док-во.
.
Док-во.
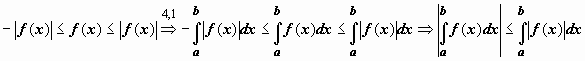 .
Теорема о
среднем. Если
f(x) непрерывна на отрезке [a,b], то существует
точка
.
Теорема о
среднем. Если
f(x) непрерывна на отрезке [a,b], то существует
точка
![]() ,
такая что
,
такая что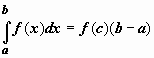 .
Док-во. Функция, непрерывная на отрезке,
принимает на этом отрезке своё наименьшее
m и наибольшее M значения. Тогда
.
Док-во. Функция, непрерывная на отрезке,
принимает на этом отрезке своё наименьшее
m и наибольшее M значения. Тогда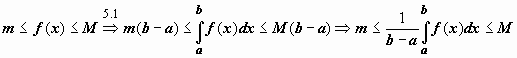 .
Число
.
Число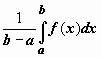 заключено
между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между m и M. Таким образом, существует
точка
заключено
между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между m и M. Таким образом, существует
точка![]() ,
такая что
,
такая что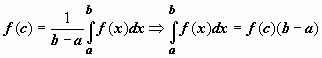 .
Это свойство имеет простую геометрическую
интерпретацию: если
.
Это свойство имеет простую геометрическую
интерпретацию: если![]() непрерывна
на отрезке [a,b], то существует точка
непрерывна
на отрезке [a,b], то существует точка![]() такая,
что площадь криволинейной трапеции
ABCD равна площади прямоугольника с
основанием [a,b] и высотой f(c) (на рисунке
выделен цветом).
такая,
что площадь криволинейной трапеции
ABCD равна площади прямоугольника с
основанием [a,b] и высотой f(c) (на рисунке
выделен цветом).