1*. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.

Пусть на некотором промежутке задана функция .

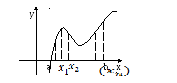
Произведём разбиение отрезка точками . Внутри каждого отрезка возьмём произвольную точку .

- интегральная сумма.

Устремим . Максимум - мелкость разбиения (характеристика разбиения). (по М.В.Д это - ∆, далее, во всех вопросах, будет использоваться и то и другое обозначения, чтобы не исправлять все лямбды в формулах).

Фигура под кривой называется криволинейной трапецией.

- определение определенного интеграла (если предел существует).

Интегральные суммы и их свойства:

Нижняя интегральная сумма: , где

Верхняя интегральная сумма: , где

1) , при данном конкретном разбиении.

2) если разбиение T' получается из разбиения T добавлением одной точки разбиения, то нижняя интегральная сумма может только увеличиться, а верхняя только уменьшиться, т.е.

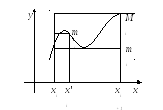
Следствие: при добавлении к любому разбиению T любого дополнительного числа точек разбиения нижняя интегральная сумма может только увеличиться, а верхняя - только уменьшиться.

3) Для любых 2-х разбиений T' и T'', нижняя интегральная сумма любого разбиения не превосходит интегральную сумму другого разбиения .

Доказательство: по предыдущему свойству рассмотрим разбиение T, полученное из всех точек разбиения T' и T''. Тогда . Аналогично. И т.к., то, что и требовалось доказать.

4) Все нижние интегральные суммы ограничены сверху, а все верхние интегральные суммы ограничены снизу. Как известно, множество чисел, ограниченных сверху имеют точную верхнюю грань аналогично и для ограниченных снизу - нижняя грань .

- верхняя грань для s (нижний интеграл Дарбу, именно так! Точная верхняя грань нижних инт.сумм = нижний инт.Дарбу).

- нижняя грань для S (верхний интеграл Дарбу).

Геометрический смысл определенного интеграла - это площадь фигуры, ограниченной прямыми , осью и графиком функции.

Основные свойства определённого интеграла.

1) - не зависит от названия переменной

2)

3) ;

4)

5) ; (следует из определения интеграла как предела интегральных сумм).

6) Если f(x) и g(x) интегрируемы на [a,b], то f(x)∙g(x) интегрируемы на [a,b]

7) Если [a,b] разбить точкой C на два интервала: [a,c] и [c,b], то:

- Из интегрируемости f(x) на [a,b] => интегрируемость f(x) на [a,c] и [c,b],

- Из интегрируемости f(x) на [a,c] и [c,b] => интегрируемость f(x) на [a,b],

-

8) Если f(x) интегрируема на [a,b] и для , то

9) Если f(x) интегрируема на [a,b], то |f(x)| интегрируема на [a,b] и ;

2**. Ограниченность интегрируемой функции.

Если функция интегрируема на отрезке, то она ограничена на этом отрезке.

Замечание: условие ограниченности является необходимым условием интегрируемости функции по Риману на отрезке.

Доказательство:

От противного. Предположим, что функция не ограничена на [a,b], при составлении интегральной суммы

_{, если ф-я не ограничена => она не ограничена по крайней мере на одном отрезке разбиения, поэтому в выражении для σ по крайней мере одно из слагаемых неограниченно => вся сумма неограниченна => lim σ не равен конечному числу, т.е. интеграл не существует. Противоречие.}

3**(-). Критерий интегрируемости ограниченной на отрезке функции.

Необходимое и достаточное условие существования опред.интеграла состоит в том, что для такое разбиение отрезка, чтоS-s≤ε.

Необходимость: 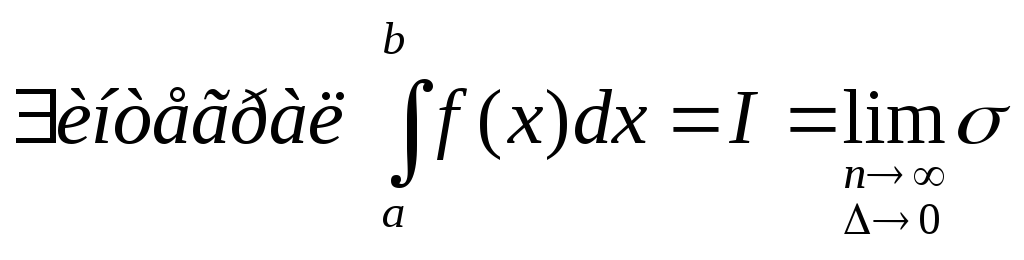. Доказать, что длятакое разбиение отрезка, чтоS-s≤ε.

Т.к. существует lim σ = I => оценим разностьS-s = S – σ + σ – I + I – s:

|S – s| ≤ |S – σ| + |I – σ| + |I – s| ≤ (соответственно:) ε/4 (почему?) + ε/4 (по определению предела) + ε/4 (почему?) ≤ ¾ ε < ε

Достаточность: дано: разбиение:S – s<ε. Доказать, что ф-я интегрируема, т.е. .

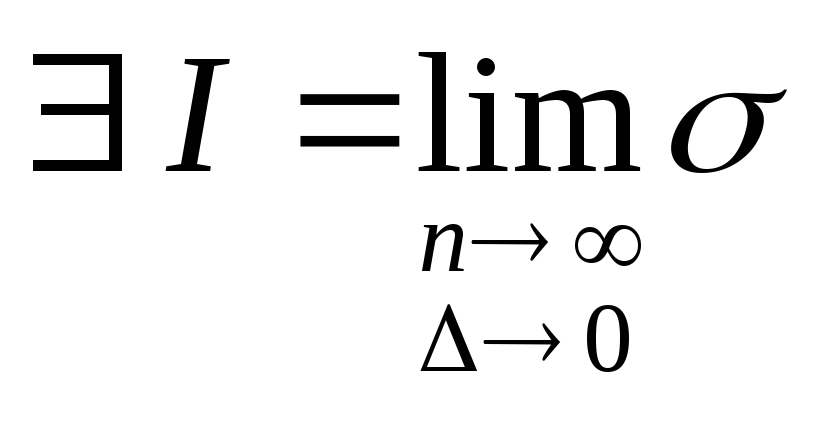S – s < ε

- для в.и.Дарбу при такое разбиение, чтоS – ≤ ε/2 (из определения inf S)

Аналогично для : притакое разбиение, что–s≤ ε/2 (из определения sup s)

Складываем неравенства: S – + –s ≤ ε, но нам дано, что S – s<ε =>

–≤ε => = = I => S – I < ε => lim S = I => I = lim σ.