37. Оператор Гамильтона. (набла) его применение (примеры).

Оператор набла (оператор Гамильтона) – векторный дифференциальный оператор, обозначаемый символом . Для трёхмерного евклидова пространства в прямоугольных декартовых координатах оператор набла определяется следующим образом:

Для трёхмерного евклидова пространства в прямоугольных декартовых координатах. оператор набла определяется следующим образом:

, где — единичные векторы по осям x, y, z.

Через оператор набла естественным способом выражаются основные операции векторного анализа: grad (градиент), div (дивергенция), rot (ротор), а также оператор Лапласа (см. ниже). Широко употребляется в описанном смысле в физике и математике (хотя иногда графический символ используется также для обозначения некоторых других, хотя в некотором отношении не совсем далеких от рассмотренного, математических объектов, например, ковариантной производной).

Под n-мерным оператором набла подразумевается вектор с компонентами в n-мерном пространстве.

38. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (оду) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.

Дифференциальным уравнением называется соотношение , в котором x – независимая переменная, y – искомая функция. Это обыкновенное дифференциальное уравнение (ОДУ) первого порядка.

– уравнение, разрешённое относительно производной.

f(x,y) – заданная, непрерывная в некоторой области D переменных (x,y) функция.

Пусть. График функции называется интегральной кривой, – изоклины кривые.

Пусть правая часть уравнения (*) не зависит от y, то есть , тогда .

На рисунке представлено семейство интегральных кривых, зависящих от одного параметра C.

Пусть . Будем считать независимой переменной y, а x – функция от y, то есть . Тогда. Но если и это уравнение имеет корень , то добавляется решение, которое надо добавить к общему семейству, зависящему от параметра C.

Всякая функция вида при подстановке в (*), после чего (*) становится тождеством, является решением (общим решением дифференциального уравнения (*)).

Если C взято равным конкретному числу, то решение φ(x,C0) называется частным решением уравнения (*). - отсюда находится значение C.

Условие Коши – когда указано, какому x0 соответствует y0. Задача Коши: – условие уравнения + условие Коши, то есть . Задачу Коши геометрически можно сформулировать так: среди всех интегральных кривых уравнения (*) найти ту кривую (рисунок слева), которая проходит через заданную точку (x0, y0).

Пример. Дано: и . Решить задачу Коши.

Когда , то :

– частное решение задачи Коши.

39++. Интегрирование ОДУ первого порядка с разделяющимися переменными и однородных.

Уравнением с разделенными переменными называется дифференциальное уравнение вида: с непрерывными функциями f(х) и g(y). Равенство , где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.

Принцип решения таких уравнений:

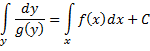
Если дано условие Коши, то есть и , то. Если и уравнение имеет корень , то это решение добавляется к основному семейству.

Определение однородной функции. Функция f(x,y) называется однородной функцией своих переменных x и y, если, каково бы ни было число , выполняется следующее: , где p – степень (показатель) однородности. Например, – однородная функция, степень однородности p = 3, так как . Степень p может быть равной нулю, если .

Уравнение называется однородным, если функция, стоящая в правой части, является однородной функцией своих переменных. Пусть f(x,y) будет однородной функцией степени 0, то есть . Пусть , тогда . Уравнения такого типа решаются заменой (переходом к новой функции): .

– общее решение.

Если , а , то:

Если , то уравнение имеет корень u0, тогда: – решение: – прямая наряду с семейством.

Общий вид однородного уравнения, если его записать в виде дифференциалов:

То есть M(x,y) и N(x,y) должны быть однородными функциями одной и той же степени однородности.

40++. Интегрирование линейных ОДУ первого порядка и уравнения Бернулли.

ДУ первого порядка называется линейным, если неизвестная функция y(x) и её производная y’(x) входят в уравнение в первой степени: . P(x), Q(x) – непрерывные функции. Уравнение однородное, если Q(x)=0.

Форма вариации производной постоянной: (1), обнуляем правую часть

. Общее решение уравнения:. Находим производную . Подставим y и y’ в уравнение (1):

, :.

Уравнения Бернулли имеют следующий вид:

Принцип решения:

Если обозначить за Z(x), то . Отсюда . Подставим это выражение выше и получим:

Получили дифференциальное линейное уравнение, принцип решения которого рассмотрен выше.

Пример: , ,

41++. Интегрирование ОДУ первого порядка в полных дифференциалах. Интегрирующий множитель.

Дано уравнение вида

Если левая часть есть дифференциал некоторой функции u(x,y): – общий интеграл уравнения; если , а , то критерий полного дифференциала .

Предположим, что критерий выполняется. Найдём эту функцию u. Пусть , тогда . Так как , то . Отсюда находится φ'(y).

Пример: +

Интегрирующий множитель.

– неполный дифференциал.

Существует ли функция (интегрирующий множитель) по умножению на которую (*) станет полным дифференциалом?

Если найдены два интегрирующих множителя и , то – решение.

Если зависит только от x

Пример:

;

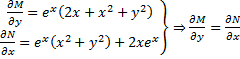
Интегрирующие комбинации:

42++. Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.

Уравнения, не разрешённые относительно производной, выглядят так: .

Уравнения первого порядка n-ой степени решаются так:

Если из уравнения y можно выразить, то есть , то это решается методом введения параметра, а именно: Обозначим, получим:

Продифференцируем по x:

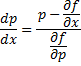
Получили уравнение, разрешённое относительно производной. p(x,C) подставляем в (*), получим: . Это и будет решение.

Рассмотрим теперь случай, когда из уравнения можно явно выразить x, то есть . Вводим параметр , получаем . Дифференцируем по y обе части:

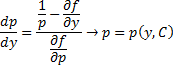
Мы получили уравнение, разрешённое относительно производной . В итоге получаем: .

Уравнение Лагранжа – это уравнение, линейное относительно x и y, оно имеет вид: . Уравнения Лагранжа ВСЕГДА интегрируется в квадратурах.

Принцип решения: Вводим параметр , получаем:

Пусть , поделим всё выражение на A(p):

Продифференцируем по x:

, т.к. :

Получили линейное уравнение первого порядка. Отсюда находим .

В итоге решение в параметрическом виде:

Отдельно рассмотрим случай, когда :

Если это тождество, то есть , то:

Если это не тождество, а уравнение с корнями: например, p₀ – корень, то есть , тогда – решение.

Частный случай уравнения Лагранжа – это уравнение Клеро. Это когда уравнение Лагранжа имеет следующий вид: . Принцип решения: Вводим параметр , получаем . Дифференцируем по x, получаем:

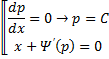
Общее решение уравнения Клеро:

Здесь – семейство всевозможных кривых; – огибающая этого семейства, тоже является решением и называется особое решение.