
Задание 4.1 – 4.10.
4.1. Составить уравнение линии, расстояния каждой точки которой от начала координат и от точки А(5; 0) относятся как 2 : 1. Сделать чертеж.
4.2. Составить уравнение линии, для каждой точки которой ее расстояние до точки F(– 1; – 2) равно расстоянию от прямой х = – 3. Сделать чертеж.
4.3. Составить уравнение линии, расстояние каждой точки которой от точки А(– 1; 0) вдвое меньше расстояния ее от прямой х = – 4. Сделать чертеж.
4.4.
Составить уравнение линии, для каждой
точки которой отношение расстояний до
точки F(7;
0)
и прямой х
= 1
равно

 .
Сделать чертеж.
.
Сделать чертеж.
4.5. Составить уравнение линии, расстояния каждой точки которой от точки А(2; 0) и от прямой 5х + 8 = 0 относятся как 5 : 4. Сделать чертеж.
4.6.
Составить уравнение линии, для каждой
точки которой отношение расстояний до
точки F(2;
0)
и прямой х
= 3
равно

 .
Сделать чертеж.
.
Сделать чертеж.
4.7. Составить уравнение линии, каждая точка которой находится вдвое дальше от точки А(4; 0), чем от точки В(1; 0). Сделать чертеж.
4.8. Составить уравнение линии, для каждой точки которой ее расстояние до точки F(3; 3) равно расстоянию от прямой у = – 2. Сделать чертеж.
4.9. Составить уравнение линии, расстояния каждой точки которой от точки А(2; 0) и от прямой 2х + 5 = 0 относятся как 4 : 5.
4.10.
Составить уравнение линии, для каждой
точки которой отношение расстояний до
точки F(2;
0)
и прямой
 равно 2.
Сделать чертеж.
равно 2.
Сделать чертеж.
Задание 5.1 – 5.10. Найти пределы функций
5.1.
1)
 при а) х0
= 3, б)
х0
= ∞;
2)
при а) х0
= 3, б)
х0
= ∞;
2)
 ;
;
3)
 4)
4)
 5)
5)

5.2.
1)
 при а)
х0
= 2, б)
х0
= ∞;
2)
при а)
х0
= 2, б)
х0
= ∞;
2)
 ;
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
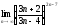 .
.
5.3.
1)
 при а)
х0
= – 3, б)
х0
= ∞;
2)
при а)
х0
= – 3, б)
х0
= ∞;
2)
 ;
;
3)
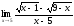 ;
4)
;
4)
 ;
5)
;
5)
 .
.
5.4.
1)
 при а)
х0
= – 2, б)
х0
= ∞;
2)
при а)
х0
= – 2, б)
х0
= ∞;
2)
 ;
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 .
.
5.5.
1)
 при а) х0
= 4,
б) х0
= ∞;
2)
при а) х0
= 4,
б) х0
= ∞;
2)
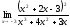 ;
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 .
.
5.6.
1)
 при а) х0
= 5,
б) х0
= ∞;
2)
при а) х0
= 5,
б) х0
= ∞;
2)
 ;
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
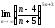 .
.
5.7.
1)
 при а) х0
= – 4,
б) х0
= ∞;
2)
при а) х0
= – 4,
б) х0
= ∞;
2)
 ;
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 .
.
5.8.
1)
 при а) х0
= – 5,
б) х0
= ∞;
2)
при а) х0
= – 5,
б) х0
= ∞;
2)
 ;
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 .
.
5.9.
1)
 при а) х0
= 1,
б) х0
= ∞;
2)
при а) х0
= 1,
б) х0
= ∞;
2)
 ;
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 .
.
5.10.
1)
 при а) х0
= – 1,
б) х0
= ∞;
2)
при а) х0
= – 1,
б) х0
= ∞;
2)
 ;
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 .
.
Задание 6.1 – 6.10. Дана функция y = f(x). Требуется исследовать ее на непрерывность, найти точки разрыва, если они есть, и установить характер разрыва.
6.1.
 6.2.
6.2.

6.3.
 6.4.
6.4.

6.5.
 6.6.
6.6.

6.7.
 6.8.
6.8.

6.9.
 6.10.
6.10.

Задание 7.1-7.10. Найти производную функции:
7.1.
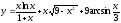 .
7.2
.
7.2
 .
.
7.3.
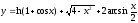 .
7.4
.
7.4
 .
.
7.5.
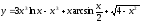 .
7.6.
.
7.6. .
.
7.7.
 .
7.8.
.
7.8.
 .
.
7.9.
 .
7.10.
.
7.10.
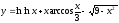 .
.
Задание 8.1-8.2. Проведите полное исследование функции и постройте ее график.
8.1 8.2
8.2
 8.3
8.3
 8.4
8.4

8.5
 8.6
8.6
 8.7
8.7
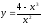
8.8
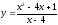 8.9
8.9
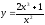 8.10
8.10

Задание
9.1-9.10.
Найти полный дифференциал функции
 .
.
9.1.
 9.2.
9.2.

9.3.
 9.4.
9.4.

9.5.
 9.6.
9.6.
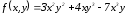
9.7.
 9.8.
9.8.

9.9.
 9.10.
9.10.

Задание 10.1-10.10. Найти неопределенные интегралы. Результаты проверить дифференцированием.
11.


12.


13.



14.


15.


16.



17.


18.


19.


20.


