Угловое ускорение тела

Пусть теперь известен закон изменения угловой скорости

и в момент времени угловая скорость тела равна, а в момент времени - .

Тогда

- приращение угловой скорости за время.

Средним угловым ускорением тела за промежуток времени называется отношение приращения угловой скорости к промежутку времени, за который это изменение произошло, т.е.

.

Алгебраическим угловым ускорением тела в данный момент времени называется предел отношения приращения угловой скорости к промежутку времени, за которое это приращение произошло, при стремлении последнего к нулю.

. (7.3)

Таким образом, алгебраическое угловое ускорение тела в данный момент времени равно первой производной по времени от алгебраической угловой скорости или второй производной от угла поворота

. (7.4)

Угловое ускорение тела характеризует быстроту изменения угловой скорости тела с течением времени.

Если знаки и совпадают, т.е., то вращение тела называется ускоренным.

Если знаки и не совпадают, т.е., то вращение тела называется замедленным.

Абсолютное значение углового ускорения будем обозначать :

.

Единица измерения углового ускорения тела в системе СИ – рад/с².

Частные случаи

1. Равномерное вращение

- условие равномерного вращения.

Определим закон движения.

Пусть при :,.

Из условия равномерного вращения следует

.

Откуда и, следовательно, закон равномерного вращения тела

2. Равнопеременное вращение твердого тела

- условие равнопеременного вращения.

Из этого условия следует

Откуда .

Из последнего следует

И, следовательно, закон равнопеременного вращения тела имеет вид .

При этом, если знаки и совпадают, то вращение называется равноускоренным, если знаки иразличны, то вращение называется равнозамедленным.

Замечание. Угловая скорость и угловое ускорение могут быть только у тела. Нельзя говорить угловая скорость или угловое ускорение точки. На первой лекции мы определили, что под материальной точкой понимают простейшую модель материального тела любой формы, размерами и вращением которого можно пренебречь. У точки есть только скорость и ускорение.

Таким образом, угловая скорость и угловое ускорение являются кинематическими характеристиками твердого тела. Определение этих характеристик, как известно из прошлой лекции, является второй основного задачей кинематики твердого тела. Перейдем к третьей задаче кинематики вращательного движения твердого тела.

Распределение скоростей и ускорений в теле при вращательном движении

Выберем в теле произвольную точку М. Обозначим ее начальное положение М₀. Проведем через нее и ось вращения неподвижную плоскость отсчета П_о. Свяжем также точку М с подвижной плоскостью П. Если закон вращательного движения задан , то положение точкиМ в момент времени t будет определяться углом . Траекторией точкиМ будет окружность, лежащая в плоскости перпендикулярной оси вращения. На рис. 7.1 изображено это сечение.

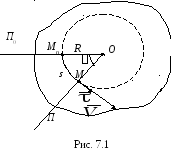
Пусть задано положительное направление отсчета угла против хода часовой стрелки в сторону движения. П₀, П – прямые пересечения соответствующие плоскостей с плоскостью сечения. Тогда зависимость дуги от угла запишется для движения точки М следующим образом

, (7.5)

где - радиус окружности, по которой движется точка.

Так как задано, то таким образом движения точкиМ будет задано естественным способом. При этом проекция вектора скорости точки на касательную равна

. (7.6)

Направление вектора скорости точки определяется направлением вращения тела:

. (7.7)

Таким образом, величина скорости равна:

. (7.8)

Скорости точек тела при его вращении вокруг неподвижной оси пропорциональны их кратчайшим расстояниям до этой оси. Скорости точек тела направлены по касательным к траекториям и, следовательно, перпендикулярны радиусам вращения.

Определим ускорение произвольной точки М при естественном способе задания ее движения (7.5). Раскладывая ускорение точки на касательную и нормальную составляющие , получим

,

.

Величина полного ускорения равна .

Таким образом, ускорение произвольной точки тела при вращательном движении вокруг неподвижной оси определяется по формулам:

, ,. (7.9)

Как видно из формул (7.9) касательное, нормальное и полное ускорения точек, как и скорости, распределены по линейному закону. Они линейно зависят от расстояний до оси вращения. Вектор нормального ускорения направлен по радиусу окружности к оси вращения (рис.7.2).

Направление вектора касательного ускорения зависит от знака алгебраического углового ускорения. Если знаки и совпадают, т.е. ,то направления векторов исовпадают, если, то векторы инаправлены противоположно друг другу.

Обозначим угол α между полным ускорением и радиусом вращения. Имеем

, (7.10)

т.е. угол α для всех точек тела один и тот же и от расстояния до оси вращения не зависит. Откладывать его следует от вектора ускорения к радиусу вращения в направлении дуговой стрелки углового ускорения, независимо от направления вращения тела.