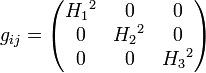FTF 2 semestr.MARTINOV / 15

Коэффициенты Ламе

Выпишем дифференциал дуги в криволинейных координатах в виде (используется правило суммирования Эйнштейна):

Принимая во внимание ортогональность систем координат ( при ) это выражение можно переписать в виде

где

Положительные величины , зависящие от точки пространства, именуются коэффициентами Ламе или масштабными коэффициентами. Коэффициенты Ламе показывают, сколько единиц длины содержится в единице координат данной точки и используются для преобразования векторов при переходе от одной системы координат к другой.

Тензор римановой метрики, записанный в координатах , представляет из себя диагональную матрицу, на диагонали которой стоя́т квадраты коэффициентов Ламе:

для i≠j

, то есть

• Правило суммирования Эйнштейна: если одна и та же буква в обозначении индекса встречается и сверху, и снизу, то такой член полагается просуммированным по всем значениям, которые может принимать этот индекс. Например, в выражении

буква i встречается и сверху, и снизу, поэтому это выражение считается эквивалентным сумме

Точнее

где n — размерность пространства, на котором определены a и b (здесь предполагается, что нумерация координат начинается с единицы).

Замечание

В некоторых случаях^[1] (если метрический тензор полагается всегда равным ) верхние и нижние индексы в формулах не различают. В таком случае суммирование ведётся по любой паре повторяющихся индексов, встречающихся в одном и том же произведении тензоров. Например, в 

Используя стандартное соглашение Эйнштейна, следовало бы писать .