FTF 2 semestr.MARTINOV / 17

Разложение вектора по базису.

Определение: Пусть  – произвольный вектор,  – произвольная система векторов. Если выполняется равенство  ,                       (1)

то говорят, что вектор  представлен в виде линейной комбинации данной системы векторов. Если данная система векторов  является базисом векторного пространства, то равенство (1) называется разложением вектора  по базису . Коэффициенты линейной комбинации  называются в этом случае координатами вектора  относительно базиса .

Теорема: (О разложении вектора по базису.)

Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.

Доказательство:

1) Пусть L произвольная прямая (или ось) и – базис . Возьмем произвольный вектор . Так как оба вектора  и  коллинеарные одной и той же прямой L, то . Воспользуемся теоремой о коллинеарности двух векторов. Так как , то найдется (существует) такое число , что  и тем самым мы получили разложение вектора  по базису  векторного пространства .

   Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису  векторного пространства :

 и , где . Тогда  и используя закон дистрибутивности, получаем:

                      .

Так как , то из последнего равенства следует, что , ч.т.д.

2) Пусть теперь Р произвольная плоскость и  – базис . Пусть  произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведемпрямую , на которой лежит вектор , прямую , на которой лежит вектор . Через конец вектора  проведем прямую параллельную вектору и  прямую параллельную вектору . Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма , и , ,  – базис ,  – базис .

   Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа , что

  и . Отсюда получаем:

 и возможность разложения по базису доказана.

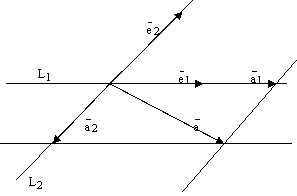
                                         рис.3.

   Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора  по базису  векторного пространства :  и . Получаем равенство

, откуда следует . Если , то , а т.к. , то  и коэффициенты разложения равны: , . Пусть теперь . Тогда , где . По теореме о коллинеарностидвух векторов отсюда следует, что . Получили противоречие условию теоремы. Следовательно,  и , ч.т.д.

3) Пусть – базис  и пусть  произвольный вектор. Проведем следующие построения.

Отложим все три базисных вектора  и вектор  от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы , плоскость  и плоскость ; далее через конец вектора  проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:

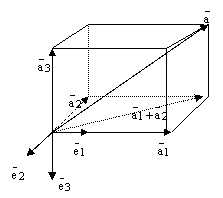
                             рис.4.

По правилу сложения векторов получаем равенство:

                        .                                    (1)

По построению . Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число , такое что . Аналогично,  и , где . Теперь, подставляя эти равенства в (1), получаем:

                                             (2)

 и возможность разложения по базису доказана.

   Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора  по базису :

 и . Тогда

       .       (3)

   Заметим, что по условию векторы   некомпланарные, следовательно, они попарно неколлинеарные.

Возможны два случая:  или .

а) Пусть , тогда из равенства (3) следует:

           .                        (4)

Из равенства (4) следует, что вектор  раскладывается по базису , т.е. вектор  лежит в плоскости векторов  и, следовательно, векторы  компланарные, что противоречит условию.

б) Остается случай , т.е. .  Тогда из равенства (3) получаем  или

             .                           (5)

Так как – базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что  и , ч.т.д.

Теорема доказана.

Контравариантные и ковариантные векторы

Контравариантные векторы

Пусть V -некоторое векторное пространство. Пусть в векторном пространстве V задан некоторый базис . Произвольный вектор  можно представить как линейную комбинацию векторов базиса: . Обозначим координаты с верхним индексом и примем правило Эйнштейна - если в выражении участвуют одинаковые разноуровневые индексы, то по ним предполагается суммирование. Таким образом можно записать: . Зададим новый базис с помощью матрицы преобразования . По тем же соображениям введем нижние и верхние индексы (чтобы не писать знаки суммирования) - . Тогда  (предполагается суммирование по индексу j). Обозначив обратную матрицу  можно записать: . Подставив эту формулу в координатное представление вектора x получим: . Таким образом координаты вектора в новом базисе оказываются равными , то есть преобразуются "противоположно" (обратно) изменению базиса. По этой причине такие векторы называют контравариантными - изменяющимися противоположно базису. Контравариантные векторы - это обычные векторы. Контрвариантные векторы в координатном представлении обычно записывают как "вектор-столбец".

Ковариантные векторы

Пространство всех линейных функционалов, отображающих векторы в числа называют сопряженным пространством V*. Оно также является векторным пространством. В этом пространстве также можно определить базис. Обозначим элементы базиса сопряженного пространства с верхним индексом . Любой функционал можно представить в этом базисе через координаты, которые будем обозначать нижними индексами. Тогда применяя правило Эйнштейна можем записать: , то есть любой линейный функционал можно записать просто набором чисел , как обычный вектор (за исключением нижнего расположения индекса).

Выберем базис в сопряженном пространстве так, что , то есть эти функционалы находят -ю координату вектора (проекцию на базисный вектор ). Такой базис называют дуальным (базису основного пространства). При смене базиса основного пространства необходимо сохранить это условие, то есть . Таким образом, дуальный базис изменяется обратно изменению основного базиса. Координаты произвольного линейного функционала  будут меняться противоположно собственному базису (как и в любом пространстве), то есть с помощью матрицы . Следовательно, они будут меняться так как основной базис! Это свойство называют ковариантностью. Сами линейные функционалы в координатном представлении в дуальном базисе называют ковекторами. Внешне ковектор "выглядит" как обычный вектор - в смысле обычного набора чисел, представляющих его координаты. Отличие ковектора от контрвариантного вектора заключается в правиле преобразования его координат при смене базиса - они преобразуются так как базис, в отличие от контрвариантных векторов, преобразующихся противоположно базису. Для идентификации ковекторов используется нижний индекс, в отличие от обычных (контравариантных) векторов. Ковекторы в координатной форме записывают как "вектор-строку".