FTF 2 semestr.MARTINOV / 11
.docx|
Дифференциальные операции второго порядка |
|
||||||||
|
Обратимся вновь к понятиям градинта, дивергенции и ротора: grad u = ∇ u , div A = ∇ A , rot A = ∇ × A. Последовательным применением оператора набла, можно образовать шесть дифференциальных операций второго порядка: ∇2 u , ∇ × ∇ u , ∇2 A , ∇ (∇ A) , ∇ (∇ × A) , ∇ × (∇ × A). При условии непрерывности функций и их производных второе и пятое выражения обращаются в нуль: ∇ × ∇ u = rot grad u = 0, ∇ (∇ × A) = div rot A = 0. Хотя эти два утверждения ранее уже были доказаны, представляется разумным проанализировать их с другой точки зрения. Если чисто формально воспринимать векторный оператор ∇ как просто вектор, то выражение ∇ × ∇ представляет собой векторное произведение двух одинаковых векторов, которое всегда равно нулю. С этих же позиций выражение ∇ (∇ × A) является смешанным произведением, содержащим два одинаковых вектора, что также всегда равняется нулю. Однако алгебра операторов в некоторых отношениях совпадает с векторной алгеброй, но имеются и существенные различия между ними. Действительно, рассмотрим вектор ∇ × ∇ u , представив его в виде разложения по базису прямоугольной системы координат:
Координаты этого вектора обращаются в нуль, если смешанные производные не зависят от порядка дифференцирования, т.е. при условии непрерывности функций и их производных. Таким образом, уравнение ∇ × ∇ u = 0 не является тождеством, а удовлетворяется только для определенного класса функций. Суммируя изложенное, представим результаты дифференциальных операций второго порядка в виде таблицы. |
|||||||||
|
|||||||||
Опера́тор Лапла́са —
дифференциальный оператор, действующий
в линейном пространстве гладких функций
и обозначаемый символом 
.
Функции 
он
ставит в соответствие
функцию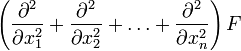 
.
Оператор
Лапласа эквивалентен последовательному
взятию операций градиента и дивергенции: 
,
таким образом, значение оператора
Лапласа в точке может быть истолковано
как плотность источников
(стоков) потенциального
векторного поля 
в
этой точке. В декартовой системе координат
оператор Лапласа часто обозначается
следующим образом 
,
то есть в виде скалярного произведения оператора
набла на
себя. Оператор Лапласа унитарен.
Формулы Грина
Формулы получаются непосредственно из теоремы о дивергенции
,
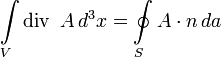которая
справедлива для любого векторного поля
А, определённого в объёме V, ограниченном
замкнутой поверхностью S. Пусть 
,
где 
и 
—
произвольные дважды непрерывно-дифференцируемые
скалярные функции. Тогда
и
,
где 
— нормальная
производная на
поверхности S (по направлению внешней
нормали по отношению к объёму V). Подставляя
(1) и (2) в теорему о дивергенции, мы придем
к первой
формуле Грина
.
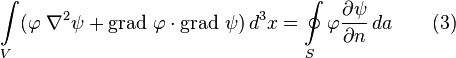Напишем
такую же формулу, поменяв в ней
местами 
и 
,
и вычтем её из (3). Тогда члены с
произведением 
сократятся
и мы получим вторую
формулу Грина,
называемую иначе теоремой
Грина:
.
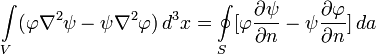