FTF 2 semestr.MAVRODI / 26

Свойства кратных интегралов

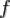Линейность по функции. Пусть измеримо, функции и интегрируемы на , тогда

.

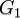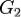Аддитивность по множеству интегрирования. Пусть множества и измеримы, 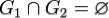и 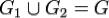. Пусть также функция 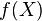определена

и интегрируема на каждом из множеств и 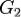. Тогда интеграл по существует и равен

.

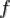Монотонность по функции. Пусть измеримо, функции и 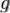интегрируемы на ,

причем 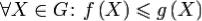. Тогда

.

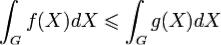Интегральное неравенство треугольника. Следствие предыдущего свойства.

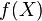Интегральная теорема о среднем. Пусть — компакт, функция непрерывна и интегрируема на , тогда

Постоянная функция 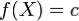интегрируема на любом измеримом множестве , причем

.

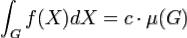Как следствие, .