FTF 2 semestr.MAVRODI / 21
.pdf
Метод неопределенных множителей Лагранжа поиска условного экстремума.
Метод Лагранжа сводится к исследованию функции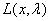 
, называемой функцией Лагранжа и
равной: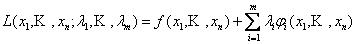
(где λţ − неизвестные постоянные параметры) на обычный локальный экстремум при наличии уравнений связи. Это позволяет решать систему с ( n + m ) неизвестными любыми методами (в том числе и на компьютере) для определения
стационарных точек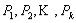 
. При проверке достаточных условий экстремума следует учитывать соотношения между дифференциалами переменных в этих точках, которые получаются
из уравнений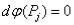 
.
Пример 1. u = x −2y +2z ; x2 + y2 + z2 − 9 = 0.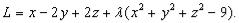 
Стационарные точки :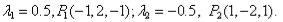
Достаточные условия: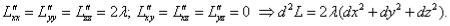 
Таким образом, в т. Р1 − минимум; в т. Р2 − максимум.
Замечание. В данной задаче второй дифференциал всегда является знакопостоянной квадратичной формой от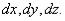 
Поэтому соотношение между дифференциалами:
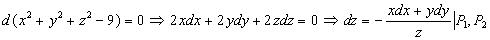не использовались при исследовании достаточного условия. Однако, в случае знакопеременного второго дифференциала указанные соотношения учитывать необходимо.
Обоснование метода Лагранжа здесь не приводится.
Пример 2.
Достаточные условия: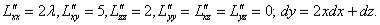 
1)
2) 
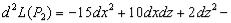знакопеременная форма 
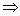экстремума нет. Замечание. Без соотношения dy = 2xdx + dz квадратичная форма и в первом случае будет знакопеременной.
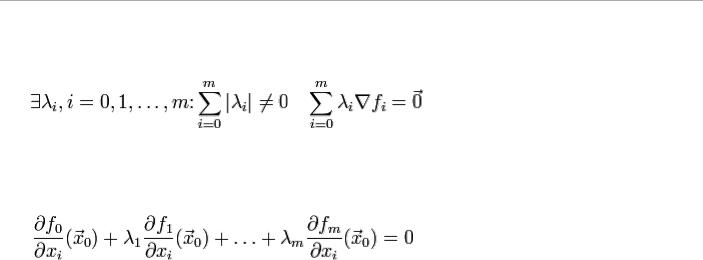
Метод множителей Лагранжа для решения задачи условного экстремума
Теорема
Пусть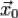 
— точка условного экстремума функции 
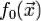при выполнении уравнений связи. Тогда в этой точке 
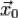градиенты 
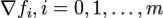являются линейно зависимыми, то
есть |
но |
. |
Следствие
Если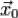 
— точка условного экстремума функции 
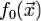относительно уравнений связи, то 
такие,
что в точке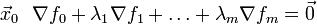 
или в координатном
виде |
. |
Достаточное условие условного экстремума
Пусть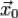 
является стационарной точкой функции Лагранжа 
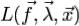при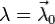 
. Если 
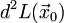— отрицательно (положительно) определена квадратическая форма переменных 
при
условии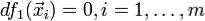 
, то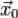 
является точкой max (min для положительно определенной) условного экстремума. Если она при этих условиях не является знакоопределенной, тогда экстремума нет.