FTF 2 semestr.MAVRODI / 49

Признак Даламбера

Признак Даламбера — признак сходимости числовых рядов. Если для числового ряда существует такое число 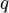, , 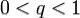что начиная с некоторого номера выполняется неравенство

то данный ряд абсолютно сходится; если же, начиная с некоторого номера

то ряд расходится.

Признак сходимости д’Аламбера в предельной форме

Замечание. Если 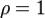, то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.

Доказательство

1.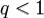, тогда существует 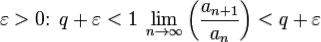, существует , для любого .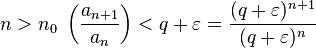

Ряд из 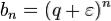сходится (как геометрическая прогрессия). Значит, ряд из сходится (по признаку сравнения).

2.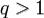, тогда существует 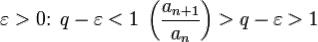. 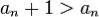для любого 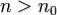. Тогда не стремится к нулю и ряд расходится.

Примеры

Ряд

абсолютно сходится для всех комплексных , так как

Ряд

расходится при всех 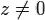, так как

Если 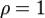, то ряд может как сходиться, так и расходиться: оба ряда 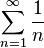и 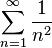удовлетворяют этому условию, причём первый ряд расходится, а второй сходится.