FTF 2 semestr.MAVRODI / 52
.pdf
Теорема Лейбница о сходимости знакочередующихся рядов
Формулировка
Теорема формулируется следующим образом. Знакочередующийся ряд сходится, если выполняются оба условия: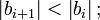 
и 
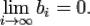
Доказательство
Допустим, что ряд начинается с положительного числа (в противном случае по приведённому ниже доказательству следует рассматривать сходимость ряда, начинающегося со второго члена).
2n-ая |
частичная |
|
|
сумма |
данного |
|
|
ряда |
|
равна |
|
|
|
|
|
|
Так как каждая сумма в |
||
скобках неположительна и |
|
то отсюда следуетограниченность 2n-ой частичной суммы сверху числом |
|
||||||
Также та же 2n-ая сумма равна |
|
|
|
|
Каждая сумма в |
||||
скобках |
неотрицательна. |
Отсюда |
следует |
неубывание |
последовательности |
то |
есть |
для |
|
любого |
выполняется |
|
|
|
|
|
|
|
|
Из первого предложения доказательства эта последовательность ограничена сверху. Значит, существует такое число s,
что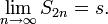 
Далее, так как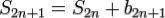 
и так как 
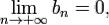то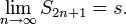 
Сумма данного ряда равна 
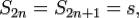где 
— конечное число. Доказательство сходимости завершено.
Следствие
Из теоремы Лейбница вытекает следствие, позволяющее оценить погрешность вычисления неполной суммы ряда:
Остаток сходящегося знакочередующегося ряда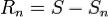 
будет по модулю меньше первого отброшенного слагаемого:
Доказательство |
|
|
|
|
|
|
Последовательность |
монотонно |
возрастающая, |
так |
как |
|
а |
выражение |
неотрицательно при любом целом |
Последовательность |
монотонно убывает, так |
|||
как |
|
а выражение в скобках неотрицательно. |
Как уже доказано при |
|||
доказательстве самой теоремы Лейбница, у обеих этих последовательностей — |
и |
— совпадающий предел |
||||
при |
Так |
получено |
|
|
и |
|
также |
Отсюда |
|
|
|
|
и |
|
|
Итак, для |
любого |
выполняется |
что и |
|
требовалось доказать. |
|
|
|
|
|
|