FTF 2 semestr.MAVRODI / 29

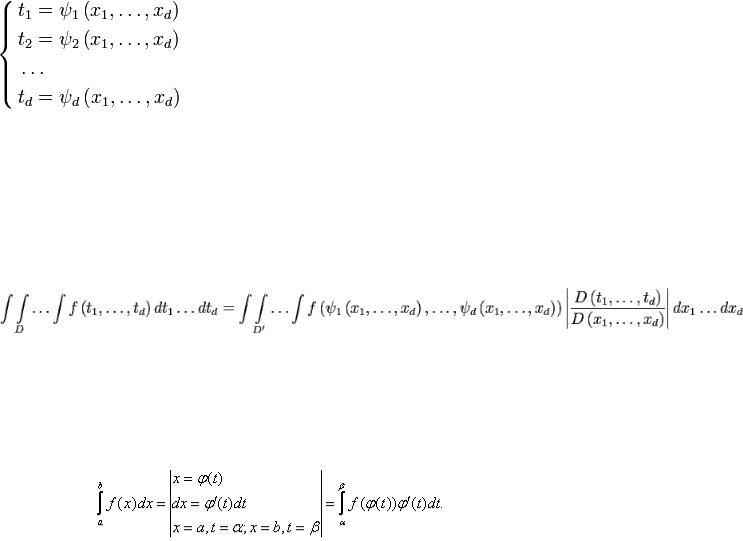
Замена переменных в кратном интеграле

Пусть задано биективное отображение 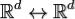, переводящее область 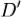в :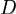

(При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством.)

,

где 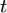— «старые» координаты, а — «новые» координаты. Пусть далее функции, задающие отображение, имеют в области 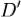непрерывные частные производные первого порядка, а также ограниченный и отличный от

нуля якобиан . Тогда при условии существования

интеграла 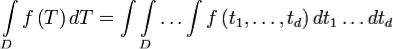справедлива формула замены переменных:

Замена переменных в двойных интегралах.

Ограничимся геометрическим обоснованием формулы замены переменных в двойном интеграле.

Вспомним сначала геометрический смысл замены переменной в однократном интеграле:

На плоскости XOY (т.е. в исходном интеграле) величина dx – элемент длины основания ступенчатой фигуры. На

плоскости TOX при разбиении отрезка элементу длины dx соответствует величина .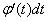

Рассмотрим теперь двойной интеграл по области D и перейдем на плоскость ,

сделав невырожденное преобразование 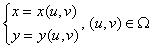(указанное преобразование переводит область 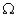в область D).

Произведение dxdy представляет собой элемент площади основания цилиндра – прямоугольник в области D. В области ему соответствует криволинейный ‘параллелограмм’, площадь которого (с точностью до бесконечно малых более высокого порядка малости) равна площади параллелограмма, построенного на векторах, касательных к его сторонам (рис.5). В свою очередь, этими касательными являются

векторы , а площадь параллелограмма – модулю их векторного произведения (см. курс аналитической геометрии) :

;

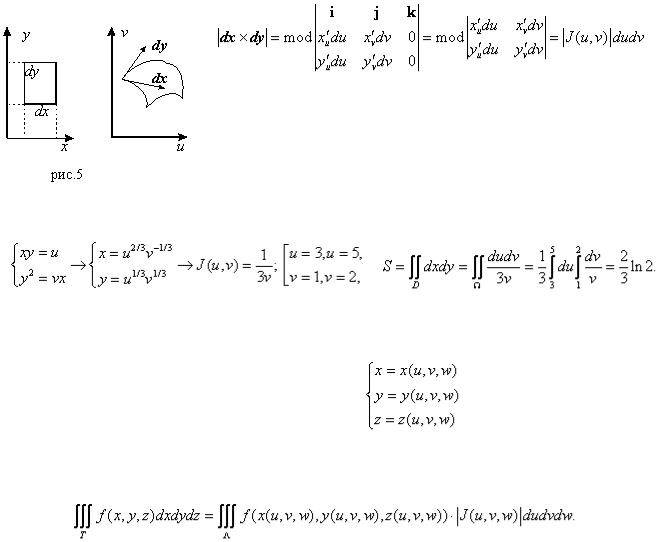
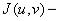( якобиан преобразования). Таким образом, окончательно имеем:

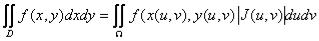− формула замены переменных в двойных интегралах.

Пример. Вычислить площадь фигуры, ограниченной линиями: 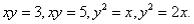(рисунок).

Замена переменных в тройных интегралах.

В тройных интегралах замена переменных проводится по тем же правилам, что и в двойных интегралах. Пусть это преобразование переводит область пространства UVW

в область T пространства XYZ . Формула замены переменных имеет вид:

(J − якобиан преобразования)