FTF 2 semestr.MAVRODI / 34

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ II РОДА

Определение криволинейного интеграла II рода

Общий вид криволинейного интеграла II рода в трехмерном случае:

(1)

где (AB) — это дуга пространственной кривой от точки A до точки B с указанным на ней направлением.

Общий вид криволинейного интеграла II рода в двумерном случае по дуге AB и по замкнутому конуру l:

при этом по умолчанию направление на фиксируется против часовой стрелки

(2)

,

Сумму слагаемых в подынтегральном выражении в криволинейном интеграле II рода принято записывать без скобок.

ОПРЕДЕЛЕНИЕ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА II РОДА В ДВУМЕРНОМ СЛУЧАЕ

1. Дугу кривой (AB) разбиваем на nэлементарных частей точками

A = M0, M1, …, Mn = B;

обозначим проекции i-той элементарной части на координатной оси:

, ;

(3)

ивычисляем ее предел при .

4.Если предел интегральной суммы существует, является конечным и не зависит ни от способа разбиения

дуги (AB) на элементарные части, ни от выбора точки на каждой элементарной части, то он называетсякриволинейным интегралом II рода по дуге (AB) от выражения 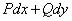и обозначается

(4)

Определение в трёхмерном случае составляется аналогично

Физическая трактовка криволинейного интеграла II рода

Если P(x,y) и Q(x,y) рассматривать как проекции на оси OX и OY вектора силы ,

то — это работа переменной силы 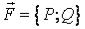, совершаемая на криволинейном перемещении (AB).

w Действительно, каждое слагаемое интегральной суммы

(3)можно трактовать как скалярное произведение

– это работа постоянной

силы на прямолинейном перемещении .

Как известно из физики, работа есть величина аддитивная. Поэтому интегральная сумма может

участки неограниченно уменьшаются, так что перемещение материальной точки совершается по кривой (AB) и под действием переменной силы , заданной в каждой точке линии (AB):

– это работа по перемещению материальной точки по кривой (AB) из положения А в

положение В под действием переменной силы v

В связи с физическим смыслом криволинейного интеграла II рода его подынтегральное выражение часто записывают в векторной форме:

(5)

,

где , , - это скалярное произведение векторов и .

Основные свойства криволинейного интеграла II рода

СВОЙСТВО 1 (линейность криволинейного интеграла II рода по подынтегральному выражению)

СВОЙСТВО 2 (АДДИТИВНОСТЬ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА II РОДА ПО ЛИНИИ ИНТЕГРИРОВАНИЯ)

,

где точка С – это любая точка на линии (АВ).

СВОЙСТВО 3 (ЗАВИСИМОСТЬ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА II РОДА ОТ НАПРАВЛЕНИЯ НА ЛИНИИ ИНТЕГРИРОВАНИЯ)

w Действительно, при изменении направления на дуге (АВ) проекции вектора изменят свои знаки, следовательно, изменит знак интегральная сумма и её предел (3). v

СВОЙСТВО 4 (ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА II РОДА)

Вычисление криволинейного интеграла II рода в двумерном случае

В каждом слагаемом интегральной суммы можно сделать преобразования по теореме Лагранжа для дифференцируемой функции одной переменной: ,

где 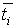— это фиксированное значение аргумента t из промежутка между точками ti-1 и ti; при этом Dxi®0 означает, что Dti®0 вследствие непрерывности функции x(t).

Выберем , что всегда возможно, так как можно выбирать произвольно на каждой части разбиения.

Если учесть, что в определении (6) означает, что 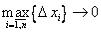, то формула (6) преобразуется к следующему виду:

.

Получился предел интегральной суммы для определенного интеграла по переменной изменяется от

значения до значения , от функции, поэтому криволинейный интеграл (6) сводится к определенному интегралу по переменной t:

Аналогично: .

Если сложить оба результата, то получится формула сведения криволинейного интеграла II рода к определенному интегралу:

(7)

где tA, tB — это значения параметра t для начала и конца линии (AB).

Аналогичная формула составляется и для трехмерного криволинейного интеграла (1) по пространственной кривой (AB):

(8)

Таким образом, вычисление криволинейного интеграла II рода сводится к вычислению определенного интеграла по параметру, через который записаны уравнения линии интегрирования (АВ). При этом в качестве параметра можно взять любую независимую переменную на линии (АВ), а далее нужно выражать всё подынтегральное выражение в криволинейном интеграле через эту независимую переменную (параметр) и её дифференциал.

Замечание

Если в двумерном случае дуга (AB) задана уравнением y = y(x), то в качестве независимой переменной (параметра) может быть взята переменная x, и формула (7) в этом случае примет следующий вид

(7')

Если же дуга (АВ) задана уравнением x = x(y), то в качестве независимой переменной (параметра) может быть взята переменная y, и тогда сведение криволинейного интеграла к определенному интегралу по yописывается следующей формулой:

(7'')

Примеры 1 (вычисление криволинейных интегралов II рода)

1.Вычислить , где (AB) — это верхняя полуокружность радиуса R, проходимая против часовой стрелки.

Решение