
FTF 2 semestr.MAVRODI / 36
.pdf
Условия независимости криволинейного интеграла второго рода от пути интегрирования (плоский случай).
Пусть в области G  задано непрерывное векторное поле (P(x,y),Q(x,y)). Например, это может быть силовое поле. Возьмем в области G две произвольные точки, А(х0,у0) и В(х,у).Соединим эти две точки
задано непрерывное векторное поле (P(x,y),Q(x,y)). Например, это может быть силовое поле. Возьмем в области G две произвольные точки, А(х0,у0) и В(х,у).Соединим эти две точки
кусочно гладкой кривой ГAB, лежащей в G. Вычислим интеграл |
Pdx + Qdy. Этот интеграл можно |
|
интерпретировать как работу силы при движении точки по кривой ГAB. Вообще говоря, |
Pdx + |
|
Qdy зависит как от точек А и В, так и от пути, по которому мы из точки А приходим в точку В. Наша цель — выяснить условия независимости величины этого интеграла (работы силы) от пути интегрирования.
Теорема 1. Следующие три условия эквивалентны: а) для любой замкнутой ломаной 
|
Pdx + Qdy = 0; |
|
|
|
|
|
|
|
|
|
||
б) |
|
Pdx + Qdy = 0 не зависит от ломаной |
, соединяющей точки А и В; |
|
|
|||||||
в) поле (P(x,y),Q(x,y)) потенциально, т. е. существует такая |
|
|
|
|||||||||
непрерывно дифференцируемая функция U(x,y) (потенциал поля), что |
|
|
||||||||||
Р(х,у)dx + Q(x,у)dy = dU, |
|
|
|
|
|
|
||||||
P(x, y) = |
|
, Q(x, y) = |
|
. |
|
|
|
|
|
|||
Доказательство проведем по круговой схеме: а)=>б)=>в)=>а). |
|
|
|
|||||||||
|
1. Докажем, что а)=>б). Пусть выполнено условие а). Возьмем две произвольных точки, А и В, в |
|||||||||||
|
|
области G. Соединим их ломаной |
. Пусть |
— любая другая ломаная, соединяющая точки |
||||||||
|
|
А и В. Тогда L = |
+ |
есть замкнутая ломаная. В силу условия а) имеем |
|
|||||||
|
|
0 = |
Pdx + Qdy = |
Pdx + Qdy + |
Pdx + Qdy = |
|
|
|
||||
|
|
= |
Pdx + Qdy - |
|
Pdx + Qdy |
|
|
|
|
|
|
|
|
|
|
Pdx + Qdy = |
Pdx + Qdy. |
|
|
|
|
|
|
||
|
|
т. е. интеграл |
Pdx + Qdy не зависит от ломаной |
, соединяющей точки А и В. |
|
|||||||
|
|
2) Докажем, что б)=>в). Пусть |
Pdx + Qdy не зависит от ломаной |
, соединяющей точки |
||||||||
|
|
А и В. Фиксируем точку А(х0,у0), а точку В(х,у) будем считать переменной. Тогда |
Pdx + |
|||||||||
|
|
Qdy зависит только от точки В, и, следовательно, в области G определена функция |
|
|||||||||
|
|
U(x, y) = |
Pdx + Qdy |
|
|
|
|
|
|
|||
Покажем, что функция U(x,y) — потенциал поля. Соединим точки В(х,у) и
С(х+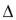 х, у) отрезком ВС, лежащим в области G (рис. 51.7). Это всегда можно сделать при достаточно малом
х, у) отрезком ВС, лежащим в области G (рис. 51.7). Это всегда можно сделать при достаточно малом  х, так как G — открытое множество. Тогда
х, так как G — открытое множество. Тогда

|
|
|
= |
|
|
|
|
= |
|
= |
|
|
|
||
= |
= |
|
|
|
|
||
|
|
Применяя при фиксированном у к непрерывной функции |
интегральную теорему о |
||||
|
|
среднем, получаем |
|
|
|
|
|
|
|
|
|
, где |
|
|
|
|
|
Воспользовавшись непрерывностью функции Р(х,у) и переходя к пределу при |
, получаем |
||||
|
|
|
|
|
|
|
|
|
|
Аналогично доказывается, что |
. |
|
|
|
|
|
|
Так как Р(х,у) и Q(x,y) — непрерывные в области G функции, то функция U(x,y)непрерывно |
|||||
|
|
дифференцируема в области G. |
|
|
|
|
|
|
2. Докажем, что в)=>а). Это следует из более общего утверждения: если |
|
|||||
|
|
||||||
|
|
Р(х,у)dx + Q(x,у)dy = dU, то для любого кусочно гладкого контура |
справедливо |
|
|||
равенство  . Действительно, если x=x(t), y=y(t),
. Действительно, если x=x(t), y=y(t),  , есть уравнение кривой
, есть уравнение кривой  , то
, то
 =
=
= =
=
= .
.
так как начало и конец замкнутой кривой совпадают.
Следствие. Если  равен нулю по любой замкнутой ломаной, то этот интеграл равен нулю и по любому кусочно гладкому контуру
равен нулю по любой замкнутой ломаной, то этот интеграл равен нулю и по любому кусочно гладкому контуру .
.
○Пусть  для любой замкнутой ломаной L. Тогда существует потенциалU(x,y) и
для любой замкнутой ломаной L. Тогда существует потенциалU(x,y) и
 .
.
Следовательно,  = 0.●
= 0.●
