FTF 2 semestr.MAVRODI / 73-74

Ядро Дирихле

Ядро Дирихле — -периодическая функция, задаваемая следующей формулой:

Данная функция является ядром, свёртка с которым даёт частичную сумму тригонометрического ряда Фурье.

Это позволяет аналитически оценивать соотношения между исходной функцией и ее приближениями в пространстве .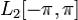

Соотношение с рядом Фурье

Пусть 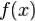— интегрируема на и -периодическая, тогда

Эта формула является одной из важнейших в теории рядов Фурье.

Доказательство

Рассмотрим n-ную частичную сумму ряда Фурье.

Применяя формулу разности косинусов к выражению, стоящему под знаком суммы, получим:

Рассмотрим сумму косинусов:

Умножим каждое слагаемое на 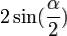и преобразуем по формуле

Применяя это преобразование к формуле (4), получим:

Сделаем замену переменного

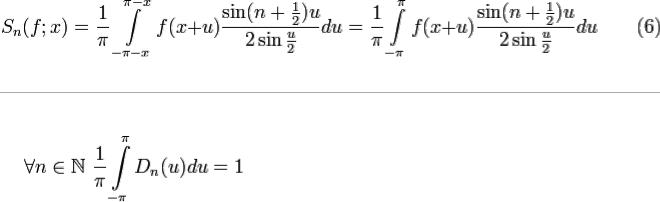
Свойства ядра Дирихле

— функция -периодическая и четная.