FTF 2 semestr.MAVRODI / 41
.pdf
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ II РОДА |
|
|
|
|
|
|
||||
Определение и физическая трактовка поверхностного интеграла II рода |
|
|
||||||||
ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТНОГО ИНТЕГРАЛА II РОДА |
|
|
|
|
||||||
В каждой точке поверхности ( ) вводится единичный |
вектор |
|
|
|
||||||
нормали |
|
|
|
и рассматривается вектор-функция |
, |
|
|
|
||
заданная |
|
своими |
|
проекциями |
на |
оси |
|
|
|
|
координат: |
|
|
|
|
. |
|
|
|
|
|
Разбив поверхность ( ) на элементарные части с площадями |
, i = 1,2,...,k и заменив эти части |
|||||||||
поверхности касательными плоскостями к ним, вычислим следующие парные произведения: |
|
|||||||||
|
|
|
|
|
|
|
|
. |
|
|
Каждое |
из |
этих |
парных |
произведений |
имеет |
смысл |
потока |
вектора |
|
|
через часть поверхности |
в направлении указанной нормали (Рис. 20). |
|
|
|
|
|||||
Вычисляя сумму составленных парных произведений и ее предел при |
|
( |
, |
- |
||||||
диаметр i-той части разбиения), получим определение поверхностного интеграла II рода: |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
(1) |
Как и при определении всех предыдущих интегралов, здесь предполагается, что предел существует, |
||||||||||
является конечным и не зависит ни от способа разбиения поверхности ( ) на элементарные части, ни |
||||||||||
от выбора точки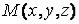 
на каждой элементарной части. Кроме этого предполагается, что
поверхность ( ) является двухсторонней и в каждой ее точке существует вектор нормали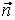 
. Определенный равенством (1) интеграл по поверхности ( ) можно записать более кратко в векторной форме:
(1')
где – это скалярное произведение векторов и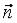 
.
Очевидно, что при положительных направляющих косинусах будут выполняться равенства:
(см. пояснение к формуле (2) предыдущего параграфа).
Поэтому существует еще одна форма записи поверхностного интеграла II рода:
(2)
При этом подинтегральное выражение в правой части принято записывать без скобок
лист Мебиуса, который получается, если прямоугольник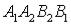 
склеить по ширине так, чтобы совпали точки A1 и B2, B1 и A2(Рис. 22)
Ориентированной
( ), на которой указана сторона поверхности
Физическая трактовка поверхностного интеграла II рода
— это поток вектора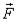 
через ориентированную поверхность ( ) в направлении ее
нормали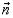 
.
Основные свойства поверхностного интеграла II рода:
СВОЙСТВО 1 (линейность поверхностного интеграла II рода по подинтегральному выражению)
СВОЙСТВО 2 (аддитивность поверхностного интеграла II рода по поверхности интегрирования)
Если |
, то |
. |
При этом все три поверхности должны быть одинаково ориентированны. |
|
|
СВОЙСТВО 3 (зависимость поверхностного интеграла II рода от ориентации поверхности)
,
то есть при изменении направления нормали к поверхности ( ) поверхностный интеграл II рода изменяет знак на противоположный.
СВОЙСТВО 4 (достаточные условия существования поверхностого интеграла II рода)
Для того, чтобы поверхностный интеграл |
существовал, достаточно выполнение |
||||
двух условий: |
|
|
|
|
|
1) векторная функция |
имеет непрерывные проекции |
, |
, |
в каждой |
|
точке поверхности |
; |
|
|
|
|
2) поверхность |
является ограниченной, двусторонней |
и имеет |
в каждой своей |
||
точке |
ненулевой вектор нормали , или, что то же, имеет в каждой своей точке касательную |
||||
плоскость. |
|
|
|
|
|
Вычисление поверхностного интеграла II рода
Вычисление поверхностного интеграла II рода в форме (2) можно проводить от каждого слагаемого в отдельности сведением к двойному интегралу по проекции поверхности ( ) на соответствующую координатную плоскость:
1.
берется знак “+” , если 
, или берется знак “–“, если 
;
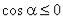функцию x = x(y,z) нужно взять из уравнения, описывающего поверхность ( ).
2.
берется знак ”+”, если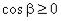 
, или берется знак “–“, если 
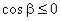; функцию y = y(x,z) нужно взять из уравнения поверхности ( ).
3.
берется знак “+”, если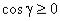 
, или берется знак “–“, если 
; функцию z = z(x,y) нужно взять из уравнения поверхности ( ) .
Если |
же |
на |
поверхности |
( |
) |
хорошо |
записывается |
единичный |
вектор |
нормали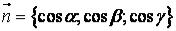 
, то криволинейный интеграл II рода проще вычислить в форме (1), так как в этом случае применяется правило вычисления поверхностного интеграла I рода (см. формулу
(2) предыдущего параграфа).
Примеры 1 (вычисления поверхностных интегралов II рода)
1. Вычислить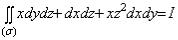 
,
где () — это внешняя часть сферы x2 + y2 + z2 = 1, заключенная в I октанте.
Решение
На внешней стороне сферы в I октанте углы , , принадлежат промежутку
[0; /2], поэтому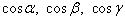 
являются неотрицательными.
На каждую из координатных плоскостей указанная часть сферы проектируется в четверть круга радиуса 1. Вычисляем интеграл от каждого слагаемого в отдельности:
.
2. Вычислить 
, где — внешняя сторона сферы x2 + y2 + z2 = 1.
Решение
— на верхней полусфере,
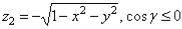— на нижней полусфере.
I = Iпо верхней полусфере + Iпо нижней полусфере =