FTF 2 semestr.MAVRODI / 51
.pdf
Критерий сходимости знакоположительных рядов (Коши)
Формулировка
Положительный ряд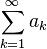 
сходится тогда и только тогда,
когда последовательность его частичных сумм |
ограничена сверху. |
Доказательство
Необходимое условие
Так как ряд сходится, то последовательность частичных сумм имеет предел. Следовательно она ограничена. А значит она ограничена и снизу и сверху.
Достаточное условие
Дан положительный ряд и последовательность частичных сумм ограничена сверху. Покажем, что наша последовательность(из членов ряда) неубывающая: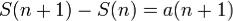 
Теперь используем свойство из теоремы о монотонной последовательности и получим, что последовательность частичных сумм сходится (она монотонно не убывает и ограничена сверху), следовательно ряд сходится
(по определению).
Строгая формулировка
Для сходимости ряда необходимо и достаточно, чтобы все отрезки этого ряда с достаточно большими номерами 
были сколь угодно малы. Другими словами, ряд 
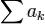сходится тогда и только тогда, когда
Доказательство
Последовательность 
частных сумм ряда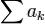 
сходится тогда и только тогда, когда она является фундаментальной, то есть
что равносильно условию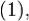 
так как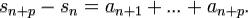 
Критерий Коши сходимости числового ряда
Теорема.
Числовой ряд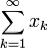 
сходится тогда и только тогда, когда для любого 
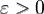существует такое 
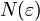, что для всех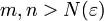 
Доказательство.
Заметим, что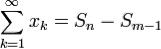 
. После этого утверждение превращается в критерий Коши сходимости последовательности 
.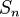