FTF 2 semestr.MAVRODI / 54

Абсолютная сходимость. Свойства абсолютно сходящихся рядов

Определение. Абсолютно сходящимся рядом называется сходящийся ряд , для которого сходится и ряд .

Легко доказать, что из сходимости ряда вытекает сходимость ряда . По

критерию Коши, примененному к ,

получаем: . Из полученного неравенства

следует, что и для исходного ряда также выполнен критерий Коши, следовательно он сходится.

равенства: . Рассмотрим ряды и . Если они сходятся,

то сходится и ряд , т.е. ряд абсолютно сходится. Если же сходятся

ряды , то, т.к. , ряды и 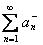тоже сходятся. Таким образом, для абсолютной сходимости необходима и достаточна

сходимость рядов и .