FTF 2 semestr.MAVRODI / 40
.pdf
ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ I РОДА: |
|
||
Определение и основные свойства поверхностного интеграла I рода |
|
||
ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТНОГО ИНТЕГРАЛА I РОДА |
|
||
Рассмотрим функцию |
, заданную в каждой точке некоторой поверхности ( ) в системе |
||
координат XOYZ. Поверхностным интегралом I рода от функции f(x,y,z) по поверхности |
|||
( ) называется конечный предел интегральной суммы при стремлении к нулю ранга разбиения, |
|||
порождающего эту сумму: |
|
|
|
|
|
(1) |
|
где n —это количество элементарных частей, на |
|
||
которые разбита поверхность ( ), |
|
|
|
i — площадь i-ой части разбиения, |
, |
|
|
— произвольная точка на i-той |
|
|
|
элементарной части (Рис.19), |
|
|
|
–– ранг разбиения, |
|
|
|
–– диаметр i-ой части разбиения. |
|
|
|
При этом предполагается, что предел интегральной суммы существует и не зависит ни от способа |
|||
разбиения поверхности ( ) на элементарные |
части, ни от выбора точек |
на каждой из |
|
элементарных частей. |
|
|
|
Основные свойства поверхностного интеграла I рода |
|
||
СВОЙСТВО 1 (ЛИНЕЙНОСТЬ ПОВЕРХНОСТНОГО ИНТЕГРАЛА I РОДА ПО ПОВЕРХНОСТИ ИНТЕГРИРОВАНИЯ)
где — постоянные по x, y, z.
СВОЙСТВО 2 (АДДИТИВНОСТЬ ПОВЕРХНОСТНОГО ИНТЕГРАЛА I РОДА ПО ПОВЕРХНОСТИ ИНТЕГРИРОВАНИЯ)
Если
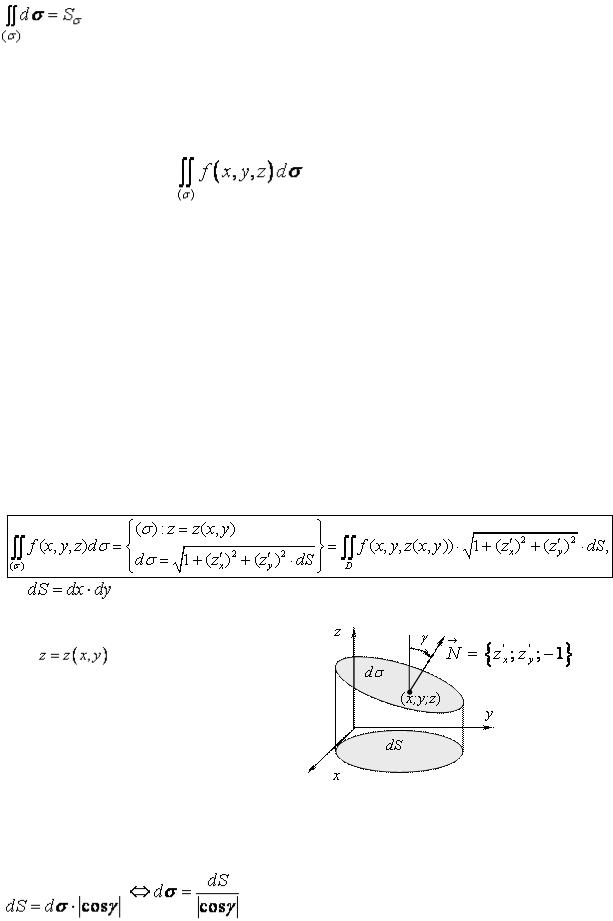
СВОЙСТВО 3 (О ЗНАЧЕНИИ ПОВЕРХНОСТНОГО ИНТЕГРАЛА I РОДА ОТ ФУНКЦИИ, ТОЖДЕСТВЕННО РАВНОЙ ЕДИНИЦЕ)
Если подынтегральная функция f(x,y,z) 1 во всех точках поверхности ( ), то поверхностный интеграл от функции f(x,y,z) по поверхности ( ) равен площади (мере) поверхности интегрирования:
СВОЙСТВО 4 (ДОСТАТОЧНЫЕ УСЛОВИЯ СУЩЕСТВОВАНИЯ ПОВЕРХНОСТНОГО ИНТЕГРАЛА I РОДА)
Если функция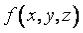 
является непрерывной в каждой точке ограниченной поверхности ( ), то
поверхностный интеграл |
существует. |
Механический смысл поверхностного интеграла I рода
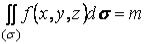— это масса неоднородной поверхности (),
если f(x,y,z)0 — это поверхностная плотность распределения массы по поверхности ().
Вычисление поверхностного интеграла I рода
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по проекции поверхности ( ) на одну из координатных плоскостей.
Например, если поверхность ( ) имеет уравнение z = z(x,y) и проектируется однозначно в область D XOY, то формула сведения поверхностного интеграла к двойному интегралу имеет такой вид:
(2)
где |
в декартовых координатах. |
Пояснения к формуле |
|
Если |
уравнение поверхности ( ) имеет |
вид: |
, то |
– это вектор нормали к поверхности в любой ее точке (x,y,z);
в окрестности этой точки бесконечно малую часть поверхности ( ) можно заменить бесконечно малой частью ее касательной плоскости, поэтому рассмотрим d как площадь бесконечно малой части касательной плоскости, проведенной к поверхности ( ) в ее точке (x,y,z);
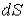- это проекция 
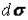на плоскость XOY; тогда по свойству проекций верно, что
;
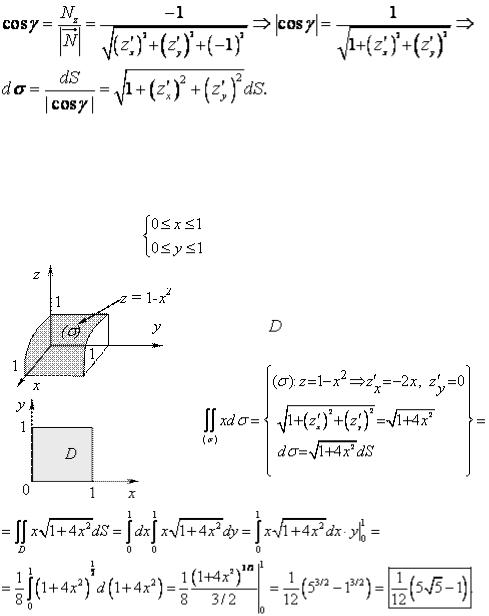
Здесь - это угол между вектором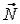 
и осью OZ, его косинус вычисляется как один из направляющих косинусов вектора 
:
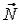Пример 1 (вычисление поверхностного интеграла I рода)
Вычислить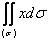 
, где ( ) - часть поверхности цилиндра
z = 1 – x2, для которой |
. |
|
|
Решение |
|
|
Строим поверхность ( ) и ее проекцию D на плоскость XOY, |
|
|
сводим данный поверхностный интеграл к двойному интегралу по |
|
|
проекции |
и вычисляем получившийся двойной интеграл: |