
FTF 1 semestr.MAVRODI / 73
.pdf
Вычисление длин кривых через определенный интеграл.
Определение спрямляемой кривой и длины кривой. Пусть на плоскости задана кривая AB. Разобьём эту кривую
точками A = M0,M1, M2, …, Mi-1, Mi, …, Mn = B на n частей и впишем в кривую ломаную M0 M1 M2 …Mi-1 Mi … Mn, соединяющую эти
точки. Длина L лом этой ломанной равна сумме длин прямолинейных звеньев, соединяющих точки разбиения:
.
Устремим теперь количество n точек разбиения к бесконечности так, чтобы максимальная длина
звена 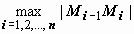 стремилась к нулю.
стремилась к нулю.
Если при этом существует конечный предел последовательности длин ломаных L лом, не зависящий от способа разбиения кривой, то кривая называется спрямляемой, а значение этого предела называется длиной кривой AB.
73.2. Длина кривой в декартовых координатах. Пусть теперь кривая AB - график функции кривой y = f(x),
имеющей непрерывную производную 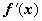 ,
, 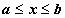 . Тогда точка M i имеет координаты (xi, f(xi)), звено Mi-1M i имеет длину
. Тогда точка M i имеет координаты (xi, f(xi)), звено Mi-1M i имеет длину
.
Функция y = f(x) на отрезке [xi-1xi] удовлетворяет условиям теоремы Лагранжа, поэтому существует
точка |
такая, что |
. |
С учётом этого длина звена Mi-1Mi равна 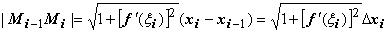 ,
,
длина всей ломаной - |
. |
|
Последняя сумма - интегральная сумма для интеграла |
, и, вследствие |
|
непрерывности подынтегральной функции, стремится к нему при |
. |
|
Итак, длина кривой, заданной декартовым уравнением y = f(x), |
, определяется |
|
формулой |
. |
|
Пример: Найти длину отрезка параболы y = x2 от точки A(0,0) до точки B(2,4).
 Решение:
Решение: 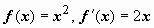 ,
,
поэтому
.

Кривая задана параметрически
.
Заменим в |
переменную x на переменную t. |
Так как |
, то |
. |
Итак, длина кривой, заданной параметрически, определяется формулой |
. |
Пример: найти длину участка развёртки окружности, соответствующего одному витку нити.
Решение: кривая задаётся
уравнениями
.
Кривая задана в полярных координатах.
Случай, когда кривая задаётся уравнением 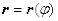 ,
, 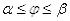 , легко сводится к предыдущему.
, легко сводится к предыдущему.
Так как 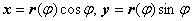 , то, рассматривая полярный угол
, то, рассматривая полярный угол  как параметр,получим
как параметр,получим
, поэтому
.
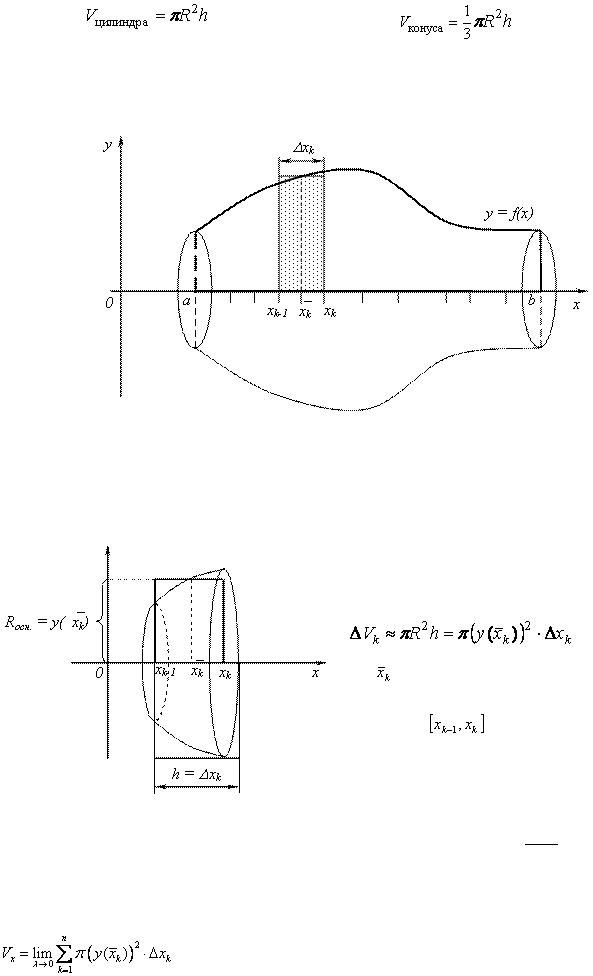
Телом вращения называется тело, получающееся при вращении плоской фигуры вокруг фиксированной оси.
Простейшие известные тела вращения – это круговой цилиндр и круговой конус:
Вычислим V тела, получающегося вращением криволинейной трапеции вокруг оси OX.
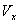 — ?
— ?
Разобьём тело вращения на элементарные части плоскостями, перпендикулярно оси вращения. Это повлечёт разбиение отрезка 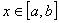 на n частей точками
на n частей точками 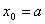 ,
, 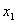 ,
, , … ,
, … ,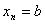 .
.
Вычислим объём каждой элементарной части (элементарный объём) приближённо как объём кругового цилиндра:
|
|
|
, |
где |
— |
некоторая |
точка, |
|
принадлежащая |
|
|
|
отрезку |
. |
|
Так как объем тела является величиной аддитивной (Аддитивность площади (или объёма) означает, что
площадь (или объём) фигуры равна сумме площадей её частей, если этих частей конечное число.), то объем всего
тела получаем суммированием элементарных объемов и переходом к пределу при всех 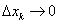 (чтобы убрать погрешность, допущенную при вычислении элементарного объема):
(чтобы убрать погрешность, допущенную при вычислении элементарного объема):
, где 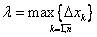 .
.
Справа в этой формуле стоит определение определенно интеграла от функции 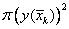 по промежутку
по промежутку 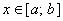 . Используя это определение, получаем формулу для вычисления объема
. Используя это определение, получаем формулу для вычисления объема
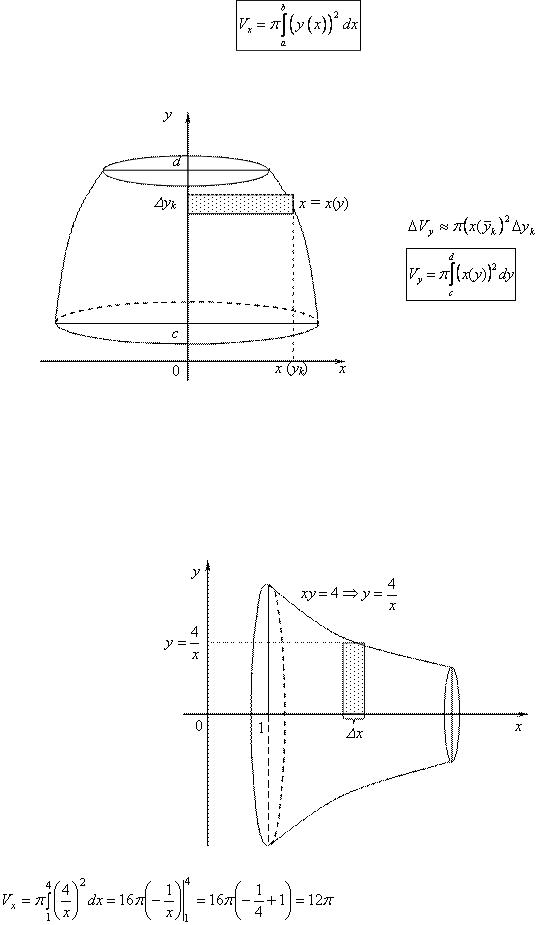
тела вращения, полученного вращением вокруг оси ОХ криволинейной трапеции, ограниченной линиями 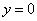 ,
, 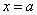 ,
, 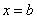 :
:
(1)
Аналогичными рассуждениями получаем формулу для объёма тела вращения вокруг оси OY:
(2)
Примеры:
1)Вычислить объём тела вращения вокруг оси OX фигуры, ограниченной линиями 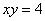 ,
, 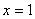 ,
,  ,
, 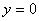 .
.
Ответ:  (единиц объёма).
(единиц объёма).
