лекцияТЭЦ_2частьИКТ_1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский государственный университет телекоммуникаций и информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

)sin k n −

.pdf

Скачиваний:

Добавлен:

10.06.2015

Размер:

1.81 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

1 /117

ТЭЦ часть 2

Лекция 1

Негармонические периодические сигналы. Разложение в ряд Фурье

	f (t)
негармоническая f (t1−0)
функция
		f (t1+0)
0	t1	t
T

Жан Батист Жозеф Фурье (Jean	Ио ганнПе терГу ставЛежён-
Baptiste Joseph Fourier) 1768-1830,	Дирихле(Johann Peter Gustav
французский математик и физик	Lejeune Dirichlet)1805-1859,
	немецкий математик

Если f (t ) – периодическая негармоническая функция, удовлетворяет условиям Дирихле, то её

можно разложить в ряд Фурье:

	a0	∞
f (t ) =		+ ∑(ak cos k ωt + bk sin k ωt ) . тригонометрическая форма

2		k =1

Функция f ( x) называется удовлетворяющей условиям Дирихле на интервале [a, b] , если она

1)непрерывна на [a, b] или имеет конечное число точек разрыва 1 рода (если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке);

2)кусочно монотонна на [a, b] , то есть отрезок [a, b] можно разделить на конечное число отрезков, внутри которых

функция f ( x) либо только возрастает, либо только убывает, либо постоянна.

Коэффициенты разложения определяются как:

t0 +T

ak =

t∫

f (t )cos k ωt dt , bk

t∫

f (t )sin k ωt dt .

f (t ) равны, то a0

= 0 .

Если площади положительных и отрицательных значений

t0 – может быть выбрано произвольно, далее полагаем t0

= 0 .

2 π

Для удобства введём переменную: α = ωt . Учитывая, что ω =

получим:

2 π

∞

f (α) =

+ ∑(ak cos k α + bk

sin k α) , где ak =

f (

α)cos k α dα , bk =

f (α)sin k α dα .

k =1

∫0

π ∫0

Если принять t0

= −

, то пределы интегрирования будут равны соответственно −π и +π .

Сумма гармоник в ряде Фурье может быть представлена в виде суммы только одних синусоид в виде функции косинуса с соответствующими начальными фазами. Для этого, пусть ak = Fk cos ψk , bk = Fk sin ψk . Подставляя в ряд Фурье, получим:

				a0	∞
			f (α) =	a0	+ ∑ Fk cos (k α − ψk ) , где
			f (α) =		+ ∑ Fk cos (k α − ψk ) , где
			2		k =1
F =
F =	a2	+ b2	– амплитуда k-ой гармоники (амплитудный спектр),
k	k	k

ψk = arctg bk – начальная фаза k-ой гармоники (фазовый спектр). ak

Представим ряд Фурье в комплексной форме:

2 /117

Поскольку: cos k α =

ejk α + e− jk α

, sin k α =

ejk α − e− jk α

2 j

= Fk cos ψk

– функция чётная, поэтому ak

= a− k ,

= Fk sin ψk

–

функция нечётная, поэтому bk

= −b− k , получаем:

f (

α) =

∞

ejk α + e− jk α

ejk α − e− jk α

+ ∑ ak

− jbk

k =1

∞

∑(ak − jbk

)ejk α +

∑(ak + jbk )e− jk α =

2 k =1

∞

−1

∞

∑(ak − jbk

)ejk α +

∑ (ak − jbk )ejk α =

∑

(ak − jbk )ejk α

∞

2 k =1

2 k =−∞

f (α) =

∑ F k ejk α , где F k

= ak − jbk

= Fk e− jψk –

комплексная амплитуда k-ой гармоники.

2 k =−∞

2 π

Поскольку a

f (α)cos k α dα , b

f (α)sin k α dα , то

∫

π ∫

= a − jb

2 π f (α)cos k α dα − j

2 π f

(α)sin k α dα =

2 π f (α)e− jk α

dα .

π ∫

∫

После возвращения к переменной t, получим:

F k =

∫ f (t )e− jk ωt dt , либо F k

∫

f (t )e− jk ωt dt –

формулы для комплексного спектра.

−

Свойства ряда Фурье

1. Функция

f (α) симметрична относительно оси ординат:

f (α)

−2

−1

f (α) =

∞

∑ak cos k α .

k =1

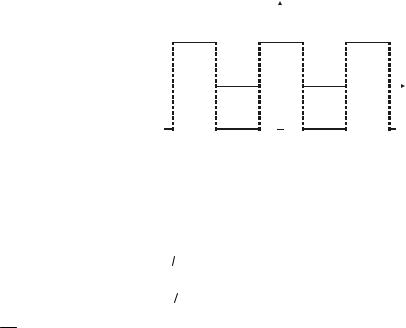
Разложим в ряд Фурье последовательность прямоугольных импульсов. Для определения коэффициентов достаточно пользоваться кривой f (α) за половину периода, то есть

f (α) = a0

π 2

k π

∫

1cos k α dα =

sin

, следовательно:

π k

∞

−π 2

cos α

cos 3α

+ ∑ ak cos k α =

cos α −

cos 3

α +

cos 5

α −…=

−

5 π

k =1

π 1

	cos 5 α
+		−… .
+	5	−… .
	5

Если функция симметрична относительно оси ординат, то разложение в ряд Фурье содержит только нечётные гармоники по закону косинуса.

2. Функция f (α) симметрична относительно начала координат:

3 /117

		f (α)
	1
−π	0	π	2π	α

∞						−1




f (α) = ∑bk sin k α .
k =1
b =	2	π	1sin k α dα = −	2	cos k α
	2			2

k	π ∫			π k
k
	0

=2 (1− cos π k ) , следовательно:

πk

∞		4		4		4
f (α) = ∑bk	sin k α =		sin α +		sin 3α +
				3 π		5 π
k =1		π

α − = 4 sin α sin 5 …

π 1

	sin 3α		sin 5 α
+		+		+… .
+	3	+	5	+… .
	3		5

Если функция симметрична относительно начала координат, то разложение в ряд Фурье содержит только нечётные гармоники по закону синуса.

3. При сдвиге начала отсчёта функции f (t ) её амплитудный спектр не изменяется, а меняется

только фазовый спектр.

Сдвинем функцию f (t )

по оси времени влево на t0 :

(

)

∞

cos

(

kω

(

t + t

0 )

− ψ

k )

∞

cos

(

kωt − ψ′

∑ k

k )

где ψ′

= ψ

− k ωt

k =1

последовательность прямоугольных импульсов сдвинута на угол π влево

В свойстве (1)

относительно последовательности прямоугольных импульсов в свойстве (2), разложение которого в ряд определяется как:

f (α) =

sin α

sin 3α

sin 5 α

+… .

С учётом свойства (3) получим:

f (α) =

sin (α + π 2)

sin 3

(α + π 2)

sin 5

(α + π 2)

cos α

+…

π 1

	cos 3α		cos 5 α
−		+		−… .
−	3	+	5	−… .
	3		5

С помощью свойства сдвига для функции, приведённой в свойстве (1) найдено её разложение в ряд Фурье, с помощью найденного разложения в ряд Фурье функции, приведённой в свойстве (2). Самостоятельно разложить в ряд Фурье последовательность пилообразных импульсов

	1	f (α)
		f (α)

				α
−π	0	π
−π			2π
	−1

4 /117

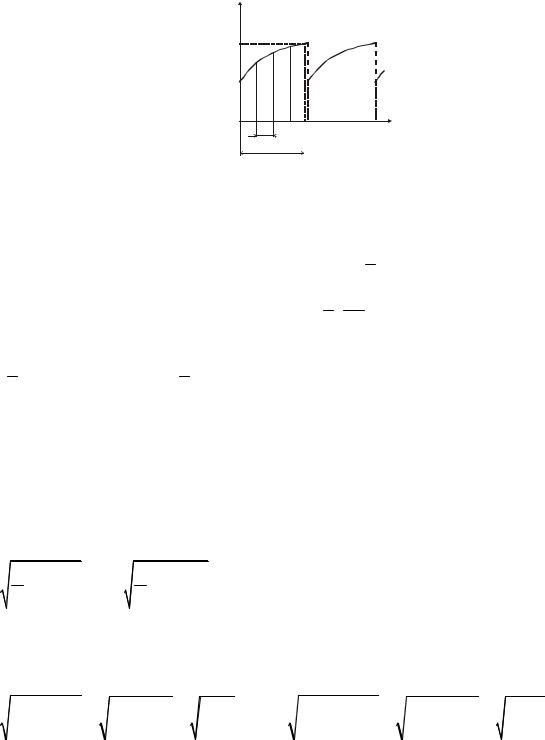
Графо-аналитический способ разложения в ряд Фурье

Данный способ применяется в случае, когда функция

f (α) имеет сложную форму.

f (α)

f (αn)

2π

4π

f (α) , равный 2 π ,

αn

Период функции

разбивается на m равных интервалов

α при этом выполняется:

m Δα = 2 π .

Расстояние от начала координат до середины n-го интервала:

αn = n Δα −

Δα

n −

Δα ,

2 π

αn = n −

Коэффициенты ряда Фурье вычисляются как:

= 1 2 π f (α)cos k α dα , b

= 1 2 π f (α)sin k α dα .

π ∫

Интегралы заменяем конечной суммой:
		2	m	1	2 π			2	m
ak	≈		∑ f (αn )cos k n −			, bk	≈		∑ f

		m n=1		2 m				m n=1

Последние два уравнения легко программируются, и при вычислении коэффициентов может использоваться ЭВМ.

Действующее, среднее значение и мощность периодического негармонического сигнала

Действующее значение определяется как

I = 1 ∫i2 (t ) dt , U = T 0

1 ∫u2 (t ) dt . T 0

Мгновенные значения периодических негармонических изменений тока и напряжения:

∞

i (t ) = I0 + ∑ Imk cos (k ωt − ψik )

, u (t ) = U0 + ∑Umk cos (k ωt − ψuk ) .

k =1

Таким образом, получаем:

∞ 2

∞

I = I02 + ∑

Imk

= I02 + ∑ Ik2 =

∑ Ik2 ,

U = U02 + ∑

Umk

= U

02 + ∑Uk2 =

∑Uk2 .

k =1 2

k =1

k =0

k =1

k =0

Вывод: действующее значение периодического негармонического сигнала определяется действующими значениями его гармоник и не зависит от их начальных фаз.

Среднее значение периодического негармонического сигнала определяется как:

	1	T		1	T
< I >=	1	∫i (t ) dt , < U >=		1	∫u (t ) dt .
< I >=	T	∫i (t ) dt , < U >=		T	∫u (t ) dt .
	T	0		T	0
		0			0
						1	T
Активная мощность негармонического сигнала: P =						1	∫u (t )i (t ) dt
Активная мощность негармонического сигнала: P =						T	∫u (t )i (t ) dt
						T	0
							0
Мгновенные значения представим как:
				∞			∞
			i (t ) = ∑ Imk cos (k ωt − ψik ) , u (t ) = ∑Umk cos (k ωt − ψik + ϕk ) ,
				k =0		k =0

где ϕk – фазовый сдвиг между током и напряжением k-ой гармоники.

/117

Выражение для активной мощности будет в виде:

∞

Ik cos ϕk

∞

P = ∑Uk

= ∑ Pk

[Вт].

k =0

Вывод: средняя за период активная мощность периодического негармонического сигнала равна

сумме мощностей отдельных гармоник.

Реактивная мощность и полная мощность периодического негармонического сигнала

определяются соответственно:

∞

Q = ∑Uk Ik sin ϕk = ∑Qk

[ВАр], S = U I =

∑Uk2 ∑ Ik2 [ВА].

k =0

Для периодических негармонических сигналов: S =

P2 + P2

+ Q2

иск

где Pиск – мощность искажений.

Характеристики формы периодических негармонических сигналов

Периодические негармонические сигналы характеризуются рядом коэффициентов:

1. Коэффициент формы – отношение действующего значения к среднему значению:

kф =

< I

< U >

2. Коэффициент амплитуды –

отношение максимального значения к действующему значению:

= Imax

= Umax .

3. Коэффициент искажения –

отношение действующего значения первой (основной)

гармоники

к действующему значению всего сигнала.

= I1

= U1 .

4. Коэффициент

гармоник

–

отношение

действующего

значения

высших

гармоник

к действующему значению основной гармоники.

∞

∑ Ik2

∑Uk2

kг =

k =2

Пусть задано периодическое негармоническое колебание вида:

u (t ) = Um1 sin ωt + Um2 sin 2 ωt , причём Um1 = 10 B , Um2 = 5 B .

∞

Определим действующее значение по формуле: U =

U02 + ∑Umk

Um1 + Um2 = 7, 906 B .

k =1

Для удобства анализа используем переменную α = ωt , тогда

u (α) = Um1 sin α + Um2 sin 2 α = u1 (α) + u2 (α) .

Представим графики u (α) , u1 (α)

и u2 (α) :

u(α), u1(α), u2 (α)

90°

180°

270°

360°

−5

u(α)

−10

−15

0,5

1,0

1,5

2,0

Определим среднее значение напряжения u (α)

по формуле:

6 /117

< U >=

p (Um1 sin a +Um2 sin 2a) da =

2Um1

= 6,366 B .

p ∫0

7, 906

Таким образом, коэффициент формы определяется как: kф =

= 1, 242 .

< U >

6,366

Определим максимальное напряжение:

d u

= Um1 cos a + 2Um 2 cos 2 a = 0 , поскольку cos 2 a = 2 cos2 a -1, то

d a

(

-Um1 )= 0, 5 .

4Um 2 cos2 a +Um1 cos a - 2Um 2 = 0 , cos a =

Um12 + 32Um2

8Um 2

Следовательно, a = arccos (0, 5) = 600 и максимальное напряжение вычисляется как:

Umax = Um1 sin 60o +Um 2 sin120o = 12, 99 B .

Таким образом, коэффициент амплитуды определяется как: ka

Umax

12,99

= 1, 643 .

7, 906

Определим коэффициент искажения: kи

Um1

= 0,894 .

7, 906 ×

U U

∑Uk2

Um2

Определим коэффициент гармоник: kг =

k =2

= 0,5

Um1

Расчёт цепей при периодических негармонических воздействиях

При периодическом негармоническом воздействии расчёт токов (напряжений) производится для каждой из гармоник отдельно по ранее изученным методам расчёта цепей. После этого определяется результирующая реакция.

Индуктивные и ёмкостные сопротивления для k-ой гармоники определяются как:

X Lk = k w L , X Ck	=	1	, где w =	2 π	– частота основной гармоники.
		kwC
				T

Комплексное сопротивление для k-ой гармоники последовательной RLC-цепи определяется как:

Z k = R + Z Lk + Z Ck = R + j X Lk - j X Ck

= R + jk w L - j

k wC

k wL-

j×arctg

k wC

= Zk ejjk

В показательной форме: Z k =

R2 + kw L -

k wC

где Zk – полное сопротивление цепи для k-й гармоники, jk –

фазовый сдвиг между входным

током и напряжением цепи для k-й гармоники.

Пусть к последовательной RLC-цепи приложено периодическое негармоническое напряжение: u (t ) = U0 +Um1 cos (wt + y1 ) +Um3 cos (3wt + y3 ) .

Определим ток в цепи для нулевой гармоники: I0

= 0 .

Определим ток в цепи для первой гармоники: I 1 =

Um1 ejy1

Um1

j(y1

-j1 )

, то есть

Z ejj1

i1 (t ) =

cos (wt + y1

- j1 ) , где

1 2

Z1 =

R2 + w L -

–

полное сопротивление цепи для первой

w L -

гармоники, j = arctg

–

фазовый сдвиг для первой гармоники.

7 /117

Определим ток в цепи для третьей гармоники: I 3 =

Um3 ejψ3

Um3

j(ψ3

−ϕ3 )

, то есть

Z3 e

jϕ3

i3 (t ) =

cos (3wt + y3 - j3 ) , где

Z3 =

R2 +

3w L -

–

полное сопротивление цепи для

3wC

3w L -

третьей гармоники, j = arctg

3wC

– фазовый сдвиг для третьей гармоники.

Согласно принципу суперпозиции определим результирующий ток в цепи:

i (t ) = I

+ i

(t ) + i

(t ) =

Um1

cos (wt + y - j ) +

Um3

cos

(3wt + y

- j ) .

I =

Действующее значение тока определяется как:

Видно, что действующее значение тока не зависит от начальных фаз первой и третьей гармоник.

Спектры периодических негармонических сигналов

u (t)

						t
− tи	0			tи		t
2		tи	2		T

tи	– длительность импульса. N =	T	– скважность.

		tи

Определим комплексный амплитудный спектр по ранее выведенной формуле:

F k

(t )e− jk ωt

dt , то есть U k

u (t )e− jk ωt dt .

∫

−

После подстановки получим:

tи

2 E

U k

∫ E e− jk ωt dt =

∫ e− jk ωt dt =

e− jk ωt

(- jk w)

−

tи

−

tи

−

tи

2 E

− j

k ωtи

2 E

k ωtи

− j

k ωtи

- e

e 2

- e 2

(- jk w)

jk w

Последнее выражение преобразуем к виду:

k ωtи

k wtи

2 E

- e− j

2 E

sin

U k

, учитывая, что w =

tи

2 j

k w

k wtи

tи

2 E

sin

k p

2 E

sin (xk

)

k π

U k

, где xk

k p

Запишем выражение в более компактном виде:

2 π :

8 /117

U k =

2 E

f (xk

) , где

f (xk )

sin (xk )

– функция отсчётов.

Представим комплексный спектр U k , если N = 2 , E = 1 В.

1,0

0,8

0,6

0,4

0,2

−10 −9 −8 −7 −6 −5 −4 −3−2 −1

0 1

9 10 k

−0,2

−0,4

Определим амплитудный спектр: Uk = U k = 2 E f (xk ) , если N = 2 , E = 1 В.

1,0

0,8

0,6

0,4

0,2

−10 −9 −8 −7 −6 −5 −4 −3 −2 −1

0 1

9 10

Определим фазовый спектр как:

если

k p

> 0 и при k = 0,

sin

sin k p < 0 и при k > 0,

если

jk =

N = 2 .

sin k p < 0 и при k < 0,

-p, если

k p

= 0, k ¹ 0

неопределено, если sin

−10 −9 −8 −7 −6 −5 −4 −3 −2 −1

0 1

9 10

−π

Вывод: амплитудный спектр является чётной, а фазовый –

нечётной функцией частоты.

9 /117

Переходные процессы. Законы коммутации, начальные и конечные условия.

В ТЛЭЦ различают установившиеся и неустановившиеся режимы.

Установившийся режим – состояние цепи, в котором все токи и напряжения являются периодическими функциями времени, либо постоянными величинами (в цепях постоянного тока).

Переходные процессы имеют место в неустановившемся режиме. Под переходными процессами понимают переход цепи из одного установившегося режима к другому.

u (t) i (t)

I установившийся режим

II установившийся режим t→∞

t = 0 момент коммутации

Из графика видно, что теоретически время переходного процесса равно бесконечности, но на практике это время зависит от параметров цепи.

Возникновение переходных процессов обусловлено коммутацией в цепях с реактивными элементами. Коммутация – включение, выключение; переключение параметров схемы или скачкообразное изменение воздействующего сигнала.

Коммутирующее устройство на схеме изображают в виде идеального ключа, у которого при замыкании сопротивление равно нулю, а в разомкнутом состоянии равно бесконечности:


	K	K

ключ на замыкание		ключ на размыкание
Момент коммутации	называется начальным	моментом времени ( t = 0 ). В момент
коммутации действуют два закона коммутации:
I закон коммутации –	ток в индуктивности в момент коммутации не изменяется скачком, а

сохраняет значение, непосредственно предшествовавшее моменту коммутации.

iL (0+ ) = iL (0) = iL (0− ) .

IIзакон коммутации – напряжение на ёмкости в момент коммутации не изменяется скачком,

асохраняет значение, непосредственно предшествовавшее моменту коммутации.

uC (0+ ) = uC (0) = uC (0− ) .

	10	/117
С помощью законов коммутации определяются начальные условия для тока в
индуктивности и напряжения на ёмкости. Под начальными условиями понимают значения токов и
напряжений в момент коммутации.
Начальные условия, определяемые с помощью законов коммутации, называют
независимыми начальными условиями, то есть iL (0) , uC (0) .
Остальные являются зависимыми начальными условиями – определяются по законам Ома,
Кирхгофа по схеме замещения, составленной в момент коммутации t = 0 .
В момент коммутации ( t = 0 ) в общем случае индуктивность можно заменить источником
тока с J = iL (0) , а ёмкость –	источником напряжения с E = uC (0) . В частном случае при iL (0) = 0
и uC (0) = 0 индуктивность заменяется обрывом, а ёмкость – коротким замыканием.
L	J

C	E

Для качественной оценки переходного процесса важно знать и конечные условия.

Конечные условия – это значение токов и напряжений в установившемся режиме при t → ∞ .

Схемы замещения реактивных элементов для установившегося режима постоянного тока:

t→∞ C

Классический метод расчёта переходных процессов

Сущность метода состоит в составлении и решении дифференциальных уравнений для

мгновенных значений токов и напряжений на основании законов Кирхгофа.

a		×	d n f	+ a	×	d n−1 f	+ + a ×	df	+ a = s (t ) , – неоднородное дифференциальное уравнение (НДУ)
			dt			dt
	n			n−1			1 dt		0
где a0 , …, an –					коэффициенты, определяющие параметры цепи, f (t ) – реакция цепи,

s (t ) – приложенное внешнее воздействие от источника.

Решение данного уравнения ищется в виде суммы общего fсв (t ) и частного fпр (t ) решений:

f (t ) = fсв (t ) + fпр (t ) .

fсв (t ) – свободная составляющая, определяется из однородного дифференциального уравнения (ОДУ) вида:

d n f

св

+ a

n−1

d n−1 f

св

+ + a ×

св

+ a

= 0 .

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.06.2015222.72 Кб4Лекция 8Таб.doc
#
18.04.201970.66 Кб1Лекция 9. ПетрI и просвещенный абсолютизм.doc
#
14.11.201886.02 Кб3Лекция 9.doc
#
21.11.2018724.48 Кб2Лекция на 11.doc
#
26.09.20191.28 Mб5Лекция_практика_Visual Foxpro.doc
#
10.06.20151.81 Mб8лекцияТЭЦ_2частьИКТ_1.pdf
#
10.06.20151.06 Mб11лекцияТЭЦ_2частьИКТ_2.pdf
#
28.08.2019175.69 Кб6Лиманский.docx
#
10.06.2015562.3 Кб10Линейные массивы.pdf
#
17.04.2019105.47 Кб7лк_17_18_19.doc
#
10.06.201519.94 Mб157ЛК_МашЗавЯП_А4.doc