
лекцияТЭЦ_2частьИКТ_1
.pdf
51 /117
Определим входное сопротивление линии без потерь в режиме КЗ. |
||||||
|
Z вх. кз = |
U ( x) |
= |
jZ 0 I 2 sin βx |
= jZ |
0 tgβx . |
|
I ( x) |
I 2 cos βx |
||||
|
|
|
|
|
||
В режиме холостого хода Z 2 |
= ∞ , поэтому I 2 |
= 0 . |
|
|
||
U ( x) = U 2 cos βx , I ( x) = jU 2
Z 0
sin βx , следовательно U ( x) = U 2 |
cos βx , I ( x) = |
U 2 sin βx . ρ0
Определим входное сопротивление линии без потерь в режиме ХХ.

52 /117
Z вх. xx = |
U ( x) |
= |
Z 0U 2 cos βx |
= − jZ |
0ctgβx . |
|
I ( x) |
jU 2 sin βx |
|||||
|
|
|
|
|||
Линия без потерь. Смешанный режим |
||||||
Рассмотрим работу линии без потерь, если Z 2 > Z 0 . Данный режим работы называется смешанным, то есть одновременно наблюдается режим бегущей волны и режим стоячей волны.
Для оценки близости к режиму бегущей волны вводят коэффициент бегущей волны (КБВ):
КБВ = |
|
|
U |
min ( x) |
|
= |
|
U |
пад ( x) −U отр ( x) |
|
= |
1 |
− |
|
|
Ru |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
U |
max ( x) |
|
|
|
U |
пад ( x) + U отр ( x) |
|
1 |
+ |
|
|
Ru |
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Иногда на практике используют коэффициент стоячей волны (КСВ).
КCВ = |
U |
max ( x) |
|
= |
|
U |
пад ( x) + |
U |
отр ( x) |
|
= |
1 |
+ |
|
|
Ru |
|
|
. |
||
|
|
|
|
|
|||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
U min ( x) |
|
U |
пад ( x) − |
U |
отр ( x) |
1 |
− |
|
|
Ru |
|
|
|||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Область изменения данных коэффициентов: 0 ≤ КБВ ≤ 1, 1 ≤ КСВ ≤ ∞ .
Если КБВ = 0 , КCВ = ∞ – |
стоячая волна, если КБВ = 1 , КCВ = 1 – бегущая волна. |
|||||||||||||||||||||
Ранее было показано, что Ru |
= |
Z 2 |
− Z 0 |
– комплексный коэффициент отражения по напряжению. |
||||||||||||||||||
Z 2 |
+ Z 0 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1− |
|
Ru |
|
|
|
|
| Z 0 | |
1+ |
|
|
|
Ru |
|
|
|
| Z 2 | |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Следовательно: КБВ = |
|
|
|
|
|
= |
|
, |
КCВ = |
|
|
|
|
|
|
|
= |
|
. |
|||
1+ |
|
Ru |
|
|
| Z 2 | |
1− |
|
|
|
Ru |
|
|
| Z 0 | |
|||||||||
|
|
|
|
|
||||||||||||||||||

53 /117
Четвертьволновый трансформатор сопротивлений
Важным в теории цепей с распределёнными параметрами является вопрос согласованного включения отрезков линии без потерь с разными волновыми сопротивлениями. Хорошее согласование обеспечивает так называемый четвертьволновой трансформатор сопротивлений.
Уравнения передачи определяются в следующем виде:
|
λ |
= jI 2 Z 0 , |
|
λ |
= j |
|
U |
2 |
. |
|
|||||||||
U |
|
I |
|
|
|||||
|
4 |
|
|
4 |
|
|
Z |
0 |
|
Входное сопротивление будем определять как: |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
I 2 |
|
|
1 |
|
|
Z |
|
= |
|
|
4 |
= Z |
2 |
|
= Z |
2 |
. |
||
вх |
|
|
λ |
0 |
|
|
0 |
|
|||||
|
|
|
|
U 2 |
|
Z 2 |
|||||||
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
Определим величину волнового сопротивления согласующего участок линии.
|
= Z 02 |
1 |
, откуда Z 0 = |
|
. |
|
Z вх |
Z вх Z 2 |
|||||
|
||||||
|
|
Z 2 |
||||
Поскольку линии 1 и 2 имеют разные волновые сопротивления то для полного их согласования необходимо выполнить условия Z 2 = Z 02 и Z вх = Z 01 . Таким образом, волновое сопротивление согласующего участка должно быть равным: Z 0 = 
 Z 01 Z 02 .
Z 01 Z 02 .
Самостоятельно решить задачи!
1. Какой минимальной длины s надо взять отрезок линии без потерь с параметрами L0 и C0 ,
чтобы на частоте f получить из него индуктивность L?
|
|
|
|
|
|
|
|
||
|
|
C |
0 |
|
|||||
|
arctg 2πfL |
|
|
|
|
|
|||
|
|
L |
|
||||||
Ответ: Короткозамкнутый отрезок длиной s = |
|
|
|
|
|
|
|||
0 |
|
. |
|||||||
|
|
|
|
|
|
|
|
||
2πf L0C0 |
|
|
|||||||
|
|
|
|
|
|||||
2. Линия без потерь с волновым сопротивлением ρ0 |
работает на нагрузку Z2 . Определите |
||||||||
первичные параметры четвертьволнового трансформатора, обеспечивающего согласование линии.

54 /117
Ответ: L = |
|
r0 Z2 |
, C = |
1 |
|
. |
|
|
|
|
|||
0 |
3×108 |
0 |
3×108 × r0 Z2 |
|
||
Линия без искажений
Линия не будет вносить искажений, если волновое сопротивление, коэффициент ослабления и фазовая скорость не будут зависеть от частоты. Условие передачи сигнала в линии без искажений записывается через первичные параметры следующим образом:
R0 = L0 – равенство Хевисайда.
G0 C0
Волновое сопротивление:
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L0 |
|
0 |
|
+ jw |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
R0 + jwL0 |
|
|
L0 |
|
|
L0 |
|
|
|||||||
Z 0 |
= |
|
= |
|
|
|
|
|
= |
|
, |
|||||||
|
G |
+ jwC |
|
|
|
G |
|
|
|
C |
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
0 |
|
|
C0 |
|
|
0 |
|
+ jw |
|
|
|
|
|
|
|
|
|
|
|
|
C0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 0 |
= |
|
R0 + jwL0 |
|
|
G0 |
+ jwC0 |
||
|
|
|
||
|
|
|
+ jw |
L |
|
|
|
R0 |
1 |
0 |
|
|
|
R0 |
|
|||||
= |
|
|
|
|
= |
|
|
|
+ jw |
C |
|
||
|
|
|
||||
|
G0 |
1 |
0 |
|
|
|
|
|
|||||
|
|
|
|
G0 |
|
|
R0 .
 G0
G0
Вывод: волновое сопротивление не зависит от частоты. |
|
|||||||||||
Коэффициент распространения: |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
R |
|
G |
|
|
|
R |
|||
|
|
|
|
|||||||||
g0 = |
L0 |
|
0 |
+ jw C0 |
|
0 |
+ jw |
= |
L0C0 |
|
0 |
|
L0 |
C0 |
L0 |
||||||||||
|
|
|
|
|
|
|
|
|
||||
+ jw =
G0
L0C0
C0
+ jw .
Поскольку g = a + jb , то a = R |
C0 |
= G |
L0 |
. |
|
|
|
||||
0 |
0 |
L0 |
0 |
C0 |
|
|
|
||||
|
|
|
|||
Используя равенство Хевисайда, a = 
 R0G0 , b = w
R0G0 , b = w
 L0C0 .
L0C0 .
Вывод: коэффициент ослабления не зависит от частоты.
Фазовая скорость:
Ранее было показано, что vф |
= |
ω |
, отсюда vф = |
|
ω |
|
|
= |
|
1 |
|
. |
|
b |
|
|
|
|
|
|
|
||||||
|
|
|
w L C |
0 |
|
|
|
L C |
0 |
|
|
||
|
|
|
|
0 |
|
|
|
0 |
|
|
|||
Вывод: фазовая скорость не зависит от частоты.

55 /117
Лекция 5
Спектральные методы анализа нелинейных электрических цепей при гармоническом воздействии. Метод тригонометрических функций кратного аргумента
i(t) |
НЭ |
|
u(t)
Пусть на вход нелинейной резистивной цепи, описываемой ВАХ i (u ) , действует гармоническое напряжение: u (t ) = Um cos (ωt + ϕ) .
Требуется определить спектр отклика, то есть спектр тока i (t ) . Классический метод анализа заключается прямой подстановкой u (t ) в i (u ) , но эта процедура является весьма громоздкой и
сложной. Существуют следующие часто применяемые методы определения спектрального состава тока.
∙метод тригонометрических функций кратного аргумента
∙метод угла отсечки
∙метод трех и пяти ординат
Метод тригонометрических функций кратного аргумента.
Этот метод применим в случае полиномиальной аппроксимации ВАХ. Рассмотрим воздействие на нелинейный резистивный элемент, ВАХ которого аппроксимирована полиномом:
i (u ) = a0 + a1u + a2u2 + ... + anun ,
гармонического колебания u (t ) = Um cos (ωt + ϕ) . Осуществляя прямую подстановку, получаем:
|
|
i (u ) |
= a + a U |
m |
cos (ωt + ϕ) |
+ a U 2 cos2 |
|
(ωt + ϕ) + ... + a U n |
cosn |
(ωt + ϕ). |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
m |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Понизим порядок данного полинома через тригонометрические функции кратных |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
аргументов, полагая α = ωt + ϕ . Так как cos2 α = |
1+ cos 2α |
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ cos 2α |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
α = cos α |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
cos α + |
|
|
cos 2α cos α . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
2 |
( |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Учитывая, что cos a cos b = |
1 |
|
|
cos |
|
a − b |
|
|
+ cos |
|
|
a + b |
|
|
|
|
|
имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
cos3 α = |
1 |
cos α + |
1 |
(cos α + cos 3α) = |
3 |
cos α + |
1 |
cos 3α . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
По аналогии можно получить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
cos4 α = |
3 |
+ |
1 |
cos 2α + |
1 |
cos 4α , cos5 α = |
5 |
cos α + |
5 |
cos 3α + |
1 |
cos 5α . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
8 |
|
2 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
16 |
|
|
|
|
|
|||||||||||||||||||||||||||
Для тока выражение приобретает вид (ограничимся 6 слагаемыми): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
i (α) = a + a U |
|
|
cos α + a U |
2 |
1+ cos 2α |
+ a U |
3 |
|
3 |
|
cos α + |
1 |
|
cos 3α |
+ |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 m |
|
|
|
|
|
|
|
|
|
|
|
2 m |
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
+a U 4 |
3 |
+ |
1 |
cos 2α + |
1 |
cos 4α |
|
+ a U |
5 |
|
5 |
cos α + |
5 |
cos 3α + |
1 |
cos 5α . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
m |
|
|
2 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Приводим подобные слагаемые: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
i (α) = a + |
1 |
a U 2 |
+ |
3 |
a U 4 |
|
+ a U |
+ |
3 |
a U 3 |
|
+ |
|
5 |
a U 5 cos α + |
1 |
a U 2 |
+ |
1 |
a U 4 |
cos 2α + |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
2 |
|
2 m |
|
|
8 |
|
|
|
|
4 m |
|
|
1 m |
|
4 |
|
3 m |
|
|
|
8 |
|
|
|
5 m |
|
|
|
|
|
|
|
|
|
2 |
|
2 m |
2 |
|
4 m |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
+ |
1 |
a U 3 |
+ |
5 |
a U 5 |
cos 3α + |
|
1 |
a U 4 |
cos 4α + |
|
|
|
1 |
a U 5 |
cos 5α. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
3 m |
16 |
5 m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 m |
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
5 m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Спектральный состав тока можно записать в виде:
i (α) = I0 + I1 cos α + I2 cos 2α + I3 cos 3α + I4 cos 4α + I5 cos 5α ,
где амплитуды гармоник определяются как:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56 |
/117 |
||
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
= a + |
1 |
a U 2 |
+ |
3 |
|
a U 4 , I = a U |
+ |
3 |
a U 3 |
+ |
5 |
a U |
5 |
, |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
2 2 m |
|
|
|
8 4 m |
1 |
|
|
1 m |
|
4 |
|
3 m |
8 |
|
5 m |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
I |
|
= |
1 |
a U 2 + |
1 |
a U 4 , I |
|
|
= |
1 |
a U 3 |
+ |
5 |
a U |
5 |
, I |
|
= |
1 |
a U 4 |
, I |
|
= |
1 |
a U 5 . |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
|
2 m |
|
2 4 m |
3 |
|
|
|
4 3 m |
16 |
|
5 m |
|
|
4 |
|
8 4 m |
|
5 |
16 5 m |
|
||||||||||||||||
|
|
|
|
Спектр тока является линейчатым, постоянная составляющая и амплитуды чётных гармоник |
|
|||||||||||||||||||||||||||||||||||||||||
определяются только чётными степенями полинома. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I0 |
|
|
|
I1 |
|
I2 |
|
I3 |
|
|
I4 |
|
|
I5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
0 |
|
|
α |
2α |
|
3α |
|
|
4α |
|
5α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Метод угла отсечки |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Данный метод применяется при кусочно-линейной аппроксимации ВАХ. Рассмотрим |
|
|||||||||||||||||||||||||||||||||||||||||
воздействие |
вида u (t ) = Um cos ωt на |
|
нелинейный |
элемент, ВАХ |
которого аппроксимирована |
|
||||||||||||||||||||||||||||||||||||||||
кусочно-линейной функцией.
Применяя метод проекций, удобно сначала, определить ток, которой бы получился в случае линейной характеристики прибора с крутизной S. Поскольку нелинейный элемент работает с отсечкой, то только заштрихованная часть напряжения участвует в создании тока. Получившиеся импульсы характеризуются следующими величинами:
Угол отсечки θ – часть периода, в течении которого ток изменяется от максимального до нулевого значения. Максимальное значение тока – Imax .
В интервале 0 ≤ ωt ≤ θ ток отличен от нуля и принимает следующее значение:

57 /117
i (t ) = KN - MN = I cos wt - I cos q = I (cos wt - cos q) .
Максимальное значение тока наблюдается в точке 0, то есть
Imax = I (1- cos q) = SUm (1- cos q) .
Периодическая последовательность импульсов i (t ) представляется в виде ряда Фурье:
i (t ) = I0 + I1 cos wt + I2 cos 2wt +... + In cos nwt.
Откуда спектральные составляющие определяются как:
I = |
1 |
θ i (t ) dwt = SU |
|
h (q) , I |
|
= |
1 |
θ i (t )cos wtdwt = SU |
|
h (q) , |
|||
2p |
|
|
|
|
|||||||||
0 |
−∫θ |
|
|
|
m |
0 |
1 |
|
p −∫θ |
m |
1 |
||
|
|
|
|
|
|
|
|
||||||
|
|
In |
= |
1 |
θ i (t )cos nwtdwt = SUmhn (q), n = 2, 3, 4... |
|
|
||||||
|
|
|
|
|
|||||||||
|
|
|
|
p −∫θ |
|
|
|
|
|
|
|
|
|
где h (q) = |
1 |
(sin q - qcos q) , h (q) = |
1 |
(q - sin qcos q) , h (q) = |
2 |
× |
sin nθ cos θ − n cos nθ sin θ |
. |
|||
|
|
|
|
||||||||
0 |
p |
1 |
p |
n |
p |
|
n |
( |
n2 |
- ) |
|
|
|
1 |
|
||||||||
Метод пяти ординат
Данный метод позволяет определить спектральный состав тока, состоящий из постоянной составляющей и амплитуд первых четырёх гармоник.
Ток в нелинейном элементе описывается уравнением вида:
i (t ) = I0 |
+ I1 cos wt + I2 |
cos 2wt + I3 cos 3wt + I4 |
cos 4wt , где w = |
2π |
. |
|
|||||
|
|
|
|
T |
|
Учитывая тот факт, что при t = 0, T , T , T , T ток приобретает значения imax , i1 , i0 , i2 , imin |
|||
6 |
4 |
3 |
2 |
соответственно, получим следующую систему из 5 алгебраических уравнений:

58 /117
Решим данную систему уравнений относительно неизвестных спектральных составляющих. Сложим и вычтем (1) и (5), получим:
imax + imin = 2I0 + 2I2 + 2I4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
imax - imin = 2I1 + 2I3 |
||||||||||
Сложим и вычтем (2) и (4), получим: |
i1 + i2 = 2I0 − I2 − I4 , |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i1 - i2 = I1 - 2I3 . |
|||||||||
Из последнего уравнения, определяя I1 = i1 - i2 + 2I3 , имеем: |
|||||||||||||||||||||||||
|
|
|
|
|
imax - imin |
= 2 (i1 - i2 + 2I3 ) + 2I3 = 2 (i1 - i2 ) + 6I3 , откуда |
|||||||||||||||||||
|
|
|
|
|
|
I3 = |
1 |
(imax - imin - 2 (i1 - i2 )) |
|
– третья гармоника тока. |
|||||||||||||||
|
|
|
|
6 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее I1 = i1 - i2 + 2 × |
1 |
|
(imax - imin |
- 2 (i1 |
- i2 )) = |
1 |
(imax |
- imin ) + |
1 |
(i1 - i2 ) . |
|||||||||||||||
|
|
|
|||||||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
||||||
Преобразуя последнее выражение, получим: |
|
|
|
|
|
|
|||||||||||||||||||
|
|
I |
= |
1 |
(i |
|
|
- i |
+ i - i |
) |
– |
первая (основная) гармоника тока. |
|||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
1 |
|
|
3 max |
|
|
min |
1 |
2 |
|
|
|
|
|
|
|
|
|
|||||||
Из (3) I0 = i0 + I2 - I4 , учитывая, что imax + imin |
= 2I0 + 2I2 + 2I4 получим: |
||||||||||||||||||||||||
|
|
|
|
|
imax + imin |
= 2 (i0 + I2 - I4 ) + 2I2 + 2I4 = 2i0 + 4I2 , откуда |
|||||||||||||||||||
|
|
|
|
|
|
|
|
I |
|
= |
1 |
(i |
+ i |
|
- 2i ) |
– |
вторая гармоника тока. |
||||||||
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
max |
min |
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку i1 + i2 = 2I0 - I2 - I4 , |
I0 = i0 + I2 - I4 , имеем: |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i1 + i2 = 2 (i0 + I2 - I4 ) - I2 - I4 = 2i0 + I2 - 3I4 . |
|||||||||||||||
Подставляя I2 в явном виде, получим:
i1 + i2 = 2i0 + 1 (imax + imin - 2i0 ) - 3I4 , откуда
4
I4 = 121 (imax + imin - 4 (i1 + i2 ) + 6i0 ) – четвёртая гармоника тока.
Определим постоянную составляющую тока, так как I0 = i0 + I2 - I4 , то
I0 |
= i0 |
+ |
1 |
(imax |
+ imin |
- 2i0 ) - |
1 |
(imax + imin - 4 (i1 + i2 ) + 6i0 ) , |
|
|
|||||||
|
|
4 |
|
|
12 |
|
||
откуда окончательно имеем:
I0 = 16 (imax + imin + 2 (i1 + i2 )) – нулевая (постоянная) гармоника тока.
Таким образом, мы определили все спектральные составляющие тока в нелинейном элементе. Построение спектра осуществляется в следующем виде:
I
|
|
|
|
|
|
I1 |
|
|
||
|
|
|
|
|
|
|
|
|||
I0 |
|
|
|
|
|
I2 |
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
I3 |
I4 I5 |
|
|
|
|
|
|
|
|
|
|
w |
|
0 |
|
|
|
w1 2w1 3w1 |
4w1 5w1 |
|||||
|
||||||||||
|
|
Модуляция. Модулированные колебания |
|
|
59 |
/117 |
|||||
|
|
|
|
|
|
||||||
Модуляция |
– |
операция |
преобразования |
низкочастотного |
первичного |
сигнала |
в |
|
|||
высокочастотный сигнал (переносчик), с сохранением содержащейся в нём информации. |
|
|
|||||||||
Передача сигнала осуществляется высокочастотными модулированными колебаниями. В |
|
||||||||||
одном периоде первичного сигнала T = 1 = 2π укладываются сотни, тысячи и более периодов |
|
||||||||||
|
|
|
|
F |
Ω |
|
|
|
|
|
|
высокочастотного |
колебания T = 1 = 2π |
. В общем случае модулированное высокочастотное |
|
||||||||
|
|
0 |
f0 |
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
колебание описывается соотношением вида: |
|
|
|
|
|
|
|||||
|
|
u (t ) = U (t )cos (ω0t + Δϕ(t ) + ϕ0 ) = U (t ) cos ψ (t ) , |
|
|
|
|
|||||
где U (t ) и ψ (t ) |
– |
амплитуда, |
мгновенная фаза |
сигнала, ω(t ) = dψ |
называют |
мгновенной |
|
||||
|
|
|
|
|
|
|
dt |
|
|
|
|
частотой колебания. Если закон изменения мгновенной частоты известен, то мгновенная фаза |
|
||||||||||
колебаний определяется как: |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
ψ (t ) = ∫ ω(t ) dt + ϕ0 , |
|
|
|
|
|
||
где ϕ0 – начальная фаза колебаний. |
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
Модуляция обычно заключается в пропорциональном первичному сигналу x (t ) |
изменении |
|
|
||||||||
параметра переносчика. Отсюда имеем следующие виды модуляций: |
|
|
|
|
|
||||||
Амплитудная модуляция (АМ) – |
состоит в пропорциональном первичному сигналу |
|
|||||||||
изменении амплитуды переносчика UАМ = U0 + ax (t ) . В результате получаем АМ колебание: |
|
|
|||||||||
|
|
uАМ (t ) = (U0 + ax (t ))cos (ω0t + ϕ0 ) . |
|
|
|
|
|
||||
В простейшем случае, когда x (t ) = X cos Ωt |
имеем следующее модулированное колебание: |
|
|
||||||||
|
|
uАМ (t ) = (U0 + aX cos Ωt )cos (ω0t + ϕ0 ) . |
|
|
|
|
|
||||
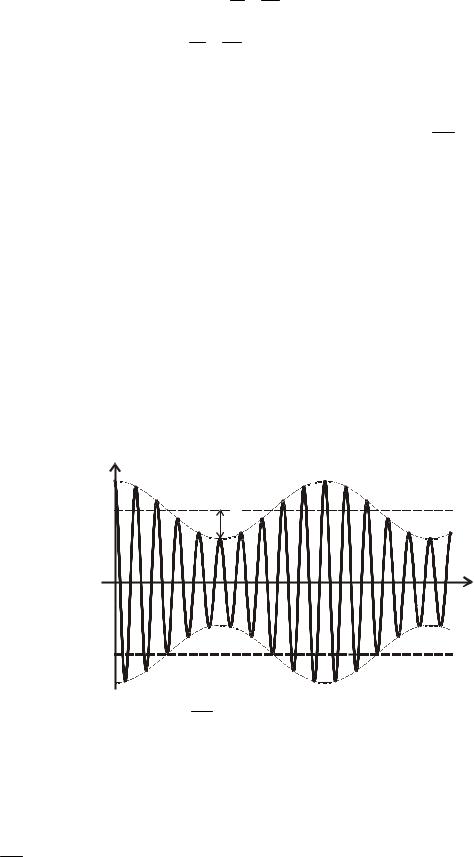
|
|
Амплитудно-модулированное колебание |
|
|
|
|
|
||||
|
|
uАМ(t) |
|
|
|
|
|
|
|
|
|
|
|
U0 |
|
UΩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
t |
|
|
|
|
|
m = UΩ |
– коэффициент модуляции. |
|
|
|
|
|
|||
|
|
|
U0 |
|
|
|
|
|
|
|
|
Отношение амплитуды огибающей к амплитуде несущего (немодулированного) колебания |
|
|
|||||||||
называют коэффициентом модуляции m. |
|
|
|
|
|
|
|
||||
Коэффициент модуляции, выраженный в процентах, называют глубиной модуляции. |
|
|
|||||||||
Коэффициент модуляции пропорционален амплитуде модулирующего сигнала. |
|
|
|
||||||||
|
|
uАМ (t ) = U0 (1+ m cos Ωt )cos (ω0t + ϕ0 ) , |
|
|
|
|
|
||||
где m = UΩ , а UΩ = aX . |
|
|
|
|
|
|
|
|
|
||
U0 |
|
|
|
|
|
|
|
|
|
|
|
Определим спектр АМ колебания: |
|
|
|
|
|
|
|
|
|||

60 /117
uАМ (t ) = U0 |
cos (ω0t + ϕ0 ) + |
m |
U |
0 cos ((ω0 |
+ Ω)t + ϕ0 ) + |
m |
U |
0 cos ((ω0 − Ω)t + ϕ0 ). |
|
|
|||||||
|
2 |
|
|
2 |
|
|
||
Спектр АМ колебания, модулированного гармоническим сигналом с частотой Ω
 U
U
U0
|
mU0 |
|
mU0 |
|
||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
ω |
|
ω0−Ω |
ω0 ω0+Ω |
||||||
Фазовая модуляция (ФМ) – заключается в пропорциональном первичному сигналу x(t) изменении фазы переносчика ϕ = ϕ0 + ax (t ) .
Частотная модуляция (ЧМ) заключается в пропорциональном первичному сигналу изменении мгновенной частоты переносчика ω = ω0 + ax (t ) .
Нелинейные модуляторы
Амплитудную модуляцию можно осуществить в нелинейных цепях. Наиболее широкое распространение получили такие устройства как нелинейные модуляторы. Представим его схему. В качестве нелинейного элемента применяется диод.
|
|
D |
|
|
|
|
|
|
|
|
|
e2(t) |
|
|
|
|
|
|
|
|
|||
|
Rэкв |
|
|
C |
|
L |
|
u (t) |
|||
|
|
|
|
|
|||||||
|
|
||||||||||
|
e1(t) |
|
|
|
|
|
|
вых |
|||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
u1 (t ) = U1 cos ω0t – |
высокочастотное напряжение, |
||||||||||
u2 (t ) = U2 cos Ωt – |
низкочастотное напряжение. |
||||||||||
ВАХ диода D аппроксимируем полиномом второй степени: i (u ) = a0 + a1u + a2u2 .
Если Rэк меньше сопротивления диода, то общее напряжение:
u (t ) = u1 (t ) + u2 (t ) = U1 cos ω0t + U2 cos Ωt .
Подставим это напряжение в ВАХ, тогда получим:
i (t ) = a0 + a1 (U1 cos ω0t + U2 cos Ωt ) + a2 (U1 cos ω0t + U2 cos Ωt )2 .
Представим спектр тока:
