Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский государственный университет телекоммуникаций и информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

лекцияТЭЦ_2частьИКТ_1

.pdf

Скачиваний:

Добавлен:

10.06.2015

Размер:

1.81 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

31 /117

i(t)

u1(t)

u (t)

(t ) = Ri (t ) = RC

duC (t )

Запишем уравнение Кирхгофа в операторной форме:

( p ) = I ( p )

+ I ( p) R = UC ( p) + UR ( p ) .

Потребуем чтобы UR ( p) UC ( p) , то есть R

, тогда U1

( p) ≈ I ( p )

, откуда

I ( p) ≈ pCU1 ( p ) .

U2 ( p) = I ( p) R = pRCU1 ( p) = τC pU1 ( p ) .

Оригинал выходного напряжения определяется: u2 (t ) = τC du1 (t ) . dt

32 /117

Интегрирующие цепи

i(t)	L
u1(t)		R	u2(t)

u2 (t ) = Ri (t ) = RL ∫0 uL (t ) dt .

U1 ( p) = I ( p ) R + I ( p) pL = UR ( p ) +UL ( p) , потребуем

чтобы UL ( p) UR ( p) , то есть pL R , тогда U1 ( p) » I ( p ) pL , откуда I ( p) »

U1 ( p)

U2 ( p) = I ( p) R =

R =

На основании теоремы об интегрировании оригинала u

(t ) =

u (t ) dt .

∫0

i(t)

(t ) =

t i (t ) dt .

u1(t)

u2(t)

∫

Запишем уравнение Кирхгофа в операторной форме:

( p ) = I ( p )

+ I ( p) R = UC ( p) +UR ( p ) .

U1 ( p)

Потребуем чтобы UC ( p) UR ( p) , то есть

R , тогда U1

( p ) » I ( p) R , откуда I ( p) »

U1 ( p)

( p) = I ( p)

, откуда оригинал u

(t ) =

(t ) dt .

tC ∫0

Частотный метод анализа переходных процессов. Преобразования Фурье

Пусть f (t ) – непериодическая

функция,

удовлетворяющая условию абсолютной

интегрируемости в бесконечных пределах, то есть

∞

(t )

f (t )

∫

dt < ¥ , при этом

< Me−ct .

−∞

f(t)			f1(t)
0	t	0	T	t
			T

Представим f (t ) в виде бесконечно большого числа малых периодических функций f1 (t ) ,

то есть f (t ) = lim f1 (t ) .

T →∞

f1 (t ) представим в виде комплексного ряда Фурье:

/117

∞

2π

f1 (t ) =

∑ Ak ejkω1t , где Ak

∫ f1 (t )e− jkω1t dt , T =

k =−∞

−

в f1 (t ) ,

и переходя к пределу T → ∞ , учитывая, что kω1 → ω ,

Осуществляя подстановку Ak

ω1 → dω , получаем:

∞

f (t ) =

∫ F (ω) ejωt dω –

ОПФ, F (

ω) = ∫ f (t )e− jωt dt – ППФ.

2π

−∞

F (ω) –

комплексная спектральная плотность, а

F (ω)

= F (ω) – спектральная плотность.

F (ω) = A(ω) − jB (ω) = F (ω)e− jφ(ω) ,

F (ω) –

амплитудный спектр, φ(ω) – фазовый спектр.

Функцию f (t ) можно представить в другой форме:

∞

f (t ) =

∫ F (ω)e− jφ(ω)ejωt dω =

∫

F (ω)cos (ωt − φ (ω))dω − j

∫ F (ω)sin (ωt − φ (ω))dω .

2π

−∞

∞

Окончательно

f (t ) =

∫ F (ω)cos (ωt − φ

(ω))dω .

Вывод: непериодический сигнал

может быть представлен пределом суммы (интегралом)

бесконечно большого числа бесконечно малых гармонических колебаний с амплитудами

F (ω)

начальными фазами φ(ω) . Спектры непериодических сигналов являются непрерывными.

Свойства преобразования Фурье

Джон Уильям Стретт, третий барон Рэлей, Лорд

Рэлей (Рэйли) (John Strutt, 3rd Baron Rayleigh), 1842-1919, британский физик

/117

∞

1. Если f (t ) – чётная функция, то спектр F (w) –

действительный. F (w) = ∫ f (t )cos wtdt .

∞

−∞

2. Взаимозаменяемость переменных t и ω . F (-t )

= ∫ f (w)ejωt dw .

∑ k

−∞

∑ k

F (w) ,

3. Теорема линейности. Если f (t ) = F (w) , то

f (t ) =

где =i – знак соответствия между сигналом и его спектром, определяемого парой преобразований

Фурье.

4. Теорема о дифференцировании сигнала. Если f

(t ) =i

(w) ,

то

f (t )

=i jwF (w) .

5. Теорема об интегрировании сигнала. Если

f (t )

=i F (w) , то

∫

f (t ) dt =i

F (w) .

−∞

6.	Теорема запаздывания (опережения). Если			f (t )		i	F	(w) , то
						=i
		i		i	1		w
7.	Теорема сжатия. Если	f (t ) =i	F (w) , то f (at ) =i			F		.
					a
							a

f (t ± t ) =i F (w)e± jωt0 .

0 i

∞

8. Теорема свёртки. Если f (t ) = F (w) , то f

(t ) f

(t ) =

−∞∫

(W) F

(w - W)dW .

Если

f (t ) = F (w) , то F (w) F (w)

∞

f (t) f

(t - t) d t .

i ∫

−∞

9. Теорема смещения. Если

F (w) , то

F (w ± W)

(t )e

jΩt

f (t ) =i

=i f

∞

10. Теорема Рэлея. W = ∫ i (t )u (t ) dt = ∫ i2 (t ) Rdt , пусть i (t ) = f (t ),

R =1 Ом, тогда

∞

−∞

∞

−∞

∞

W = ∫ f 2 (t ) dt = ∫ f (t ) f (t ) dt = ∫

f (t )×

∫ F (w)ejωt dwdt =

∫ F (w) ∫ f (t )ejωt dtdw ,

−∞

2p −∞

−∞

∞

−∞

∞

поскольку

∫ f (t )ejωt dt = F

(-w) , то W =

∫ F (w) F

(-w) dw =

∫

| F (w) |2 dw =

∫ F 2

(w) dw .

−∞

Таким образом, получаем равенство вида:

∞	(t ) dt =	1	∞	F 2 (w) dw =	1	∞	(w) dw,
∫ f 2			∫			∫ F 2
		2p			p
−∞			−∞			0

где F 2 (w) – спектральная плотность энергии сигнала.

Некоторые выкладки по теме «Свойства преобразования Фурье»

								∞
2. Взаимозаменяемость переменных t и ω F (-t ) = ∫ f									(w)ejωt dw .
		∞		−∞			∞	−∞
	1	∞		−∞	F (-w)		∞	F (-w)
f (t ) =	1	∫ F (w)ejωt dw = ∫			F (-w)	e− jωt d (-w) = ∫		F (-w)	e− jωt dw,
f (t ) =		∫ F (w)ejωt dw = ∫				e− jωt d (-w) = ∫			e− jωt dw,
	2p	−∞		+∞	2p		−∞	2p
	∞		1			1	∞
F (w) = ∫		f (t )e− jωt dt,	1	F (-w) =		1	∫ f (t )ejωt dt
F (w) = ∫		f (t )e− jωt dt,	2p	F (-w) =		2p	∫ f (t )ejωt dt
	−∞		2p			2p	−∞

Меняем местами t и ω

35 /117

∞

f (w) = ∫

F (-t )

e− jωt dt,

f (w) =

∫ F (-t )e− jωt dt,

f (w)

−∞

∞

F (-t ) =

∫ f (w)ejωt dw, F (-t ) = 2p

∫ f (w)ejωt dw, F (-t )

−∞

i	1	F (-t )
=i
=i	2p
=i	2p f (w)
i

	i		d	i
4. Теорема о дифференцировании сигнала. Если	f (t ) =i	F (w) , то		f (t ) =i	jwF (w)
4. Теорема о дифференцировании сигнала. Если	f (t ) =i	F (w) , то	dt	f (t ) =i	jwF (w)
			dt

∞

jωt

∞

jωt

∞

jωt

(t ) =

∫ F

(w)e

dw = ∫ F (w)

dw = jw ∫ F (w)e

dw=i

jwF (w)

−∞

5. Теорема об интегрировании сигнала. Если

f (t ) =i F

(w) , то

f (t ) dt =i

∫

∞

−∞

∞

∫ f

(t ) dt = ∫

∫ F (w)ejωt dwdt =

∫ F

(w) ∫ ejωt dtdw =

∫ F (w)ejωt

−∞

2p −∞

−∞

∞

(w)e

jωτ

F (w)

∫ F

dw=i

−∞

f (t ) =i

F (w) , то

6. Теорема запаздывания (смещения по времени). Если

∞

jω(t ±t0 )

∞

f (t ± t0 ) = ∫ F (w)e

dw = e

± jωt0

∫ F

(w)e

jωt

± jωt0

dw=i F (w)e

−∞

1 F (w) . jw

τ dw =

−∞

f (t ± t ) =i F (w)e± jωt0

0 i

	i		i	1	w
7. Теорема сжатия. Если	f (t ) =i	F (w) , то	f (at ) =i		F
				a
					a

f (at ) = ∞

w = aw

∞ F

w ejωt d w

∞ F

w ejωt dw=i

F (w )ejaω1t dw =

∫

w =

∫

−∞

8. Теорема свёртки. Если		f (t ) =i	F (w) , то F1 (w)
		i
∞		∞	∞ ∞
F1 (w) F 2 (w) = ∫ f1	(t)e− jωτd t ∫ f2		(q)e− jωθdq = ∫ ∫
−∞		−∞	−∞ −∞

F 2 (w)		=i		∞	(t) f2	(t - t) d t
F 2 (w)		=i		∫ f1	(t) f2	(t - t) d t
		i
				−∞			q = t - t
f	(t) f	2	(q)e− jω(τ+θ)d tdq =				q = t - t	=
1		2
							dq = dt

∞ ∞			− jω(τ+t −τ)	∞	∞				− jωt		∞
= ∫ ∫	f1 (t) f	2 (t - t)e	− jω(τ+t −τ)	dqdt = ∫	∫	f1 (t) f	2 (t - t) d t	e	− jωt	i	∫ f1 (t) f2 (t - t) d t
= ∫ ∫	f1 (t) f	2 (t - t)e		dqdt = ∫	∫	f1 (t) f	2 (t - t) d t	e		dt =i	∫ f1 (t) f2 (t - t) d t
−∞ −∞				−∞	−∞						−∞

Спектр функции Хевисайда.

∞

F (w) = ∫ lim1(t )e−ct e− jωt dt = lim ∫

1(t )e− (c+ jω)t dt = lim ∫ e− (c+ jω)t dt = lim

e− (c+ jω)t

-(c + jw)

−∞ c→0

c→0 −∞

c→0 0

c→0

= lim

(

e− (c+ jω)∞ - e− (c+ jω)0

)

= lim

(0 -1)

= lim

e− j

-(c + jw)

c→0

c→0 c + jw

jw w

∞ =

Спектры типовых сигналов

1. Спектр функции Хевисайда. Представим функцию Хевисайда в виде: 1(t ) = lim1(t ) e−ct .

c→0

∞

e− j

F (w) = lim ∫ 1(t )e− (c+ jω)t dt = lim

– комплексная спектральная плотность.

c→0 −∞

c→0 c + jw

jw w

F (w) =

– амплитудный спектр, f(w) = π – фазовый спектр.

2. Спектр δ -функции Дирака.

∞

F (ω) = ∫ δ (t )e− jωt dt = e0

= 1 , F (w) = 1 – амплитудный спектр, f(w) = 0 – фазовый спектр.

−∞

/117

Так как

∫ δ (t ) dt = 1, то F (ω) = ∫ δ (t ) dt . Взяв ОПФ δ (t ) =

∫ ejwt dω , и учитывая свойство

-¥

2π

-¥

и ω , получим: δ (ω)

взаимозаменяемости переменных t

= ∫ e± jwt dt .

f (t ) = E = const .

-¥

3. Спектр постоянного сигнала

F (ω) = ∫ Ee- jwt dt = E ∫ e- jwt dt = Eδ (ω) .

-¥

На частоте ω = 0 спектр F (0) = ∞ , на остальных частотах F (ω) = 0 .

4. Спектр гармонического сигнала

f (t ) = E cos ω0t .

jw0t

+ e

- jw0t

F (w) = ∫ E cos w0t ×e- jwt dt = E ∫

e- jwt dt =

-¥

= E

E (d(w - w0 ) + d(w + w0 ))

∫ e- j(w-w0 )t dt + ∫ e- j(w+w0 )t dt =

-¥

На частотах w = ±w0 спектр F (±ω0 ) = ∞ , на остальных частотах F (ω) = 0 .

5. Спектр прямоугольного импульса.

tи

jwtи

- jwtи

wtи

Ee- jwt dt = E 1

× 2

- e

E ×

sin

F (w) = ∫

e 2

2 =

, F

(w) = Etи

tи

2 j

wtи

F(ω)

2,0

1,6

1,2

0,8

0,4

−10

−6

ω1

ω2

10 ω

Введём понятие ширины спектра сигнала

ω :

диапазон частот, относительно которого

сосредотачивается

максимум

энергии

сигнала.

Для прямоугольного

импульса

это

–

ширина

спектра по основному лепестку:

если ω = 2π и ω = − 2π , то Δω = ω − ω = 4π .

tи

6. Спектр экспоненциального импульса.

F (ω) = ∫ e-at e- jwt dt = ∫ e-( jw+a)t dt =

- j×arctg

a .

-¥

jω + a

+ ω

Частотный анализ ЛЭЦ при непериодических воздействиях

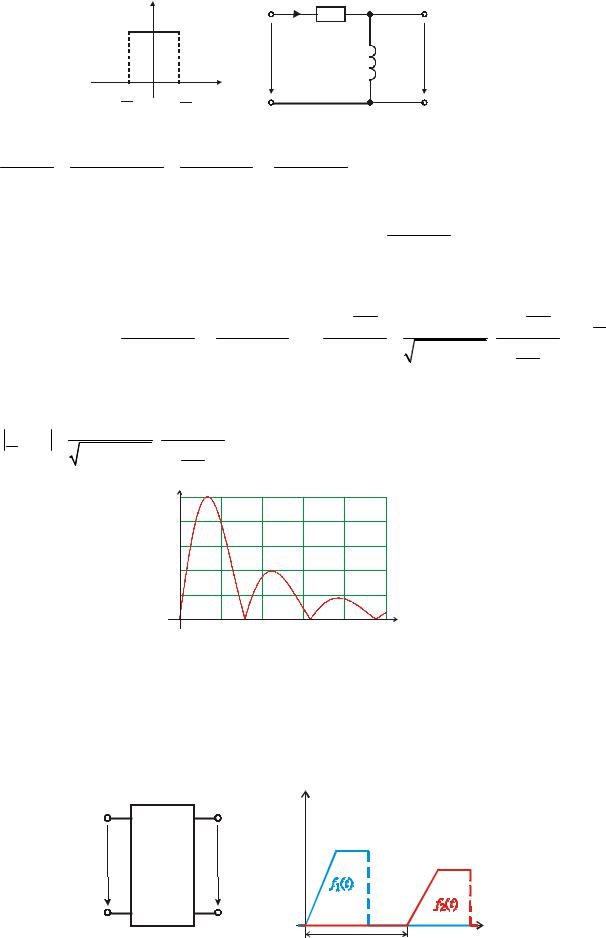
Для определения выходной реакции линейной электрической цепи используют комплексную передаточную функцию H (ω) . При этом спектр выходной реакции определяется в виде:

F 2 (ω) = H (ω) F 1 (ω) .

Рассчитаем комплексную спектральную плотность выходного сигнала U 2 (ω) в

последовательной RL -цепи, если на её вход действует сигнал в форме прямоугольного импульса.

/117

u1(t)

i(t)

u1(t)

u (t)

tи

−2

Комплексная передаточная функция определяется как:

H (w) =

jwL

jwL ( R - jwL)

(wL)2

+ j

wLR

R + jwL

R2 + (wL)2

wtи

sin

Спектральная плотность прямоугольного импульса: U 1

(w) = Etи

wtи

Комплексная спектральная плотность сигнала на выходе:

(

wtи

(w) = H (w)U

+ j

wLR

sin

j×arctg

(w) =

wL .

2 + (wL)2

R2 + (wL)2

wtи

R2 + (wL)2

wtи

Определим амплитудный спектр выходного напряжения

wtи

U2 (w) = U 2 (w) =

sin

+ (wL)

wtи

U2(ω)

Условия передачи сигнала без искажений

Сигнал на выходе устройства f2 (t ) не будет искажаться, если сохранится его форма, хотя

при этом может измениться его амплитуда и плюс ко всему сигнал запаздывает относительно

входного воздействия на t0 .

Условие безыскажённой передачи сигнала описывается в следующем виде:

f2 (t ) = kf1 (t - t0 ) ,

где t0 – время запаздывания выходного сигнала относительно входного.

			f1(t)
f (t)	ЛЭЦ	f2(t)
1
		0	t
			t0

Пусть F1 (w) – комплексный спектр на входе цепи, тогда комплексный спектр на выходе устройства в силу теоремы линейности и запаздывания записывается в виде: F 2 (w) = k F1 (w)e- jwt0 .

38 /117

Комплексная передаточная функция такой цепи будет описана: H (w) = F 2 (w) = ke− jωt0 .

F1 (w)

Вывод: электрическая цепь не будет вносить искажений, если её АЧХ является равномерной, а ФЧХ изменяется по линейному закону. Если АЧХ – неравномерная, то имеют место амплитудно-частотные искажения. Если ФЧХ – нелинейная, то имеют место фазо-частотные искажения.

Условия передачи сигналов без искажений выполняются только для резистивных цепей. В цепях с реактивными элементами такое условие можно обеспечить лишь узком диапазоне частот.

Прохождение единичного импульса через идеальный фильтр нижних частот

Единичный импульсный сигнал представим в виде:

f1(t)

f (t)	ИФНЧ	f2(t)
f (t)	ИФНЧ	f2(t)
1

0
	τ		t

Идеальный фильтр нижних частот (ИФНЧ) имеет следующие характеристики:

АЧХ: H (w) =1 , ФЧХ: j(w) = -wt0 в диапазоне частот: 0 £ w £ wc , где wc – частота среза.

H(ω)

ϕ(ω)

ωc

Комплексная передаточная функция ИФНЧ описывается: H (w) = 1×e− jωt0 .

Если длительность единичного импульса τ → 0 , то входной сигнал

f1 (t ) = d(t ) .

Так как F 1 (w) =1 , то спектральная плотность сигнала на выходе:

F 2 (w) = H (w) F 1 (w) = e− jωt0 .

Сигнал на выходе ИФНЧ определяем, взяв ОПФ:

(t - t

)

ωc

sin

− jωt0

jωt

jω(t −t0 )

ωc ( −

0 )

f2 (t ) =

∫0 e

dw =

∫0

dw =

(t - t0 )

f(t)

f2(t)

0	τ	t
	t0
С увеличением w ширина главного лепестка Dw = 4π		выходного импульса сужается, задержка
c	wc
	wc
уменьшается, амплитуда увеличивается.

39 /117

Связь между временными и частотными характеристиками

F1(ω) ЛЭЦ F2(ω)

Пусть имеется цепь с КПФ: H (ω) =

F 2

(ω)

На вход цепи действует сигнал в виде δ -функции Дирака, тогда на выходе имеем сигнал,

который численно равен импульсной характеристике. Так как F1 (ω) = 1 ,

то F 2 (ω) = H (ω) . Взяв

обратное

преобразование

Фурье, установим

связь

между импульсной

частотной

∞

характеристикой: g (t ) =

∫ H (ω) ejωt dω .

2π

−∞

∞

Прямое преобразование Фурье определяет нам КПФ: H (ω) = ∫ g (t )e− jωt dt .

−∞

Если на входе цепи действует единичная функция Хевисайда, то на выходе имеем сигнал,

численно

равный переходной характеристике.

Так как

F1 (ω) =

то F 2

(ω) =

H (ω) .

jω

Установим связь между переходной и частотной характеристикой.

∞

h (t ) =

∫

H (ω)ejωt dω .

2π

jω

−∞

40 /117

Лекция 4

Электрические цепи с распределёнными параметрами (длинные линии)

Общие сведения о регулярных линиях передачи Линия передачи (длинная линия) – устройство, ограничивающее область распространения

электромагнитных колебаний и направляющее поток электромагнитной энергии в заданном направлении.

Линия называется регулярной, если в продольном направлении неизменны её поперечное сечение, положение его в пространстве и электромагнитные свойства заполняющих её сред.

Линия является однородной, если в произвольном поперечном сечении параметры среды неизменны.

Открытые линии передачи




1	2	3	4

1 – двухпроводная линия, 2 – открытая полосковая линия, 3 – однопроводная линия, 4 – открытая диэлектрическая линия.

Закрытые линии передачи



1	2	3	4	5	6

1 – коаксиальный кабель, 2 – прямоугольный волновод, 3 – круглый волновод, 4 – эллиптический волновод, 5 – частично-заполненный волновод, 6 – экранированная полосковая линия.

Длинные линии характеризуются первичными параметрами, то есть параметрами,

отнесенными к единице длины линии. К первичным параметрам относят:

1. Резистивное сопротивление единицы длины линии

Гн

2. Индуктивность единицы длины линии L0 .м

3. Ёмкость единицы длины линии C0 .м

Cм

4. Проводимость единицы длины линии G0 .м

Ом R0 .

Телеграфные уравнения

Найдём распределения напряжения и тока в линии по её длине и во времени.

Рассмотрим элементарный участок длинной линии.

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.06.2015222.72 Кб4Лекция 8Таб.doc
#
18.04.201970.66 Кб1Лекция 9. ПетрI и просвещенный абсолютизм.doc
#
14.11.201886.02 Кб4Лекция 9.doc
#
21.11.2018724.48 Кб2Лекция на 11.doc
#
26.09.20191.28 Mб5Лекция_практика_Visual Foxpro.doc
#
10.06.20151.81 Mб8лекцияТЭЦ_2частьИКТ_1.pdf
#
10.06.20151.06 Mб12лекцияТЭЦ_2частьИКТ_2.pdf
#
28.08.2019175.69 Кб6Лиманский.docx
#
10.06.2015562.3 Кб10Линейные массивы.pdf
#
17.04.2019105.47 Кб7лк_17_18_19.doc
#
10.06.201519.94 Mб157ЛК_МашЗавЯП_А4.doc