
3_elektrichesky_tok_bez_oformlenia
.pdfЛекции по физике
1 семестр
Электрический ток

2 Постоянный ток
Постоянный ток
Электрический ток
Электрическим током называется всякое упорядоченное движение заряженных частиц или заряженных макроскопических тел. В
металлах ток создаётся свободными электронами. В проводящих растворах нет свободных электронов. Вместо них в качестве носителей тока выступают ионы. В газах могут существовать как электроны, так и ионы. Поэтому в газах ток создаётся как электронами, так и ионами. Ток в металлах, проводящих растворах и газах, обусловленный движением заряженных частиц относительно той или иной среды (внутри макроскопических тел) под действием электрического поля, называется током проводимости. Помимо тока проводимости есть конвекционный ток — движение макроскопических тел, несущих электрический заряд.
За положительное направление тока условились считать направление движения положительных зарядов. Если ток обусловлен только движением отрицательно заряженных частиц (электронов в металлах), то направление тока противоположно направлению движения зарядов.
Количественной характеристикой электрического тока служит
величина заряда, переносимого через поперечное сечение проводника в единицу времени. Её называют силой тока. Если за малое время dt
через поверхность переносится заряд q, |
то сила тока равна |
|
I |
q . |
(1) |
|
dt |
|
Ток, не изменяющийся со временем, называется постоянным. Для постоянного тока справедливо соотношение
I qt ,
где q — заряд, переносимый через рассматриваемую поверхность за конечное время t.
Электрический ток |
3 |
ВСИ единица силы тока — ампер (А) является основной. Еди-
ница заряда кулон (Кл) определяется как заряд, переносимый за
1с через поперечное сечение проводника при силе тока в 1 А.
Вобщем случае, количество заряда, протекающего через поперечное сечение проводника, может быть различно в разных частях этого сечения. Поэтому, для более детального описания тока исполь-
зуют вектор плотности тока j. Этот вектор численно равен силе
тока I через расположенную в данной точке площадку перпендикулярную к направлению движения носителей, отнесённой к площади этой площадки (dS ):
j |
I |
. |
(2) |
|
|||
|
dS |
|
|
За направление j принимается направление вектора скорости упорядоченного движения «положительных зарядов» (противоположное направлению движения отрицательных зарядов для металлов).
Поле вектора плотности тока можно изобразить с помощью линий тока, которые строятся так же, как и линии тока в текущей жидкости, линии вектора E и т.д.
Зная вектор плотности тока в каждой точке пространства, можно найти силу тока I через любую поверхность :
|
|
|
|
|
I dI j dS j ndS jn dS, |
(3) |
|||
|
|
|
|
|
где dS n dS; n — единичный вектор, перпендикулярный к поверхности dS или вектор нормали; jn jcos(j,n) j n — проекция вектора j на вектор n (на ось, направленную вдоль вектора n ).
Из (3) следует, что сила тока есть поток вектора плотности тока через поверхность или просто поток тока.
Рассмотрим поток тока через замкнутую поверхность :
jdS jndS.
Данный интеграл даёт ток, вытекающий из поверхности:
|
jdS |
|
j dS |
q |
|
dq |
, |
|
dt |
dt |
|||||||
|
n |
|
|
|||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
4 Постоянный ток
где q — заряд выходящий через поверхность , а dq — изменение заряда внутри поверхности . Применим к левой части полученного уравнения теорему Остроградского-Гаусса:
div jdV t dV
или
div j t 0.
Полученное уравнение носит название уравнение непрерывности. Для постоянных токов все электрические величины не зависят от времени и производная по времени равна нулю. Таким образом, линии постоянного тока непрерывны.
Для протекания тока проводимости в проводниках необходимо наличие в них заряженных частиц, которые могут перемещаться в пределах всего тела. Такие частицы называются носителями тока. Ими могут быть электроны, либо ионы. Второе условие возникновения тока — наличие причины, создающей упорядоченное движение зарядов. Внутри тела такой причиной служит электрическое поле.
Сторонние силы
Ток возникает при условии, что внутри тела существует электрическое поле. Под действием электрического поля возникает перемещение положительных зарядов в сторону убывания потенциала. Если ток создаётся заряженным конденсатором, то разность потенциалов при этом уменьшается и ток может прекратиться, если не отводить заряды от пластины с меньшим потенциалом к пластине с большим потенциалом (поддерживать постоянную разность потенциалов). Электростатическое поле с этой задачей справиться не может, так как оно перемещает заряды всегда так, чтобы разности потенциалов уменьшались.
Для получения постоянного тока, силы, осуществляющие такой перенос зарядов, должны иметь неэлектростатическое происхож-
дение. Они имеют общее название сторонние силы. Устройство,
Сторонние силы |
5 |
которое поддерживает постоянную разность потенциалов на концах проводника, и в котором возбуждаются сторонние силы,
называется источником тока. Источниками тока служат: генераторы, гальванические элементы, аккумуляторы, фото- и термоэлементы. В источниках тока различные виды энергии превращаются в электрическую энергию.
Движения заряженных частиц — носителей тока непосредственно не видно. Однако протекание по проводнику тока можно определить по тем действиям, которые он оказывает. Рассмотрим важнейшие действия. Во-первых, это магнитное действие, состоящее в том, что проводник с током создает вокруг себя магнитное поле, способное воздействовать на магниты (воздействие на магнитную стрелку) и другие проводники с током. Во-вторых, тепловое действие, заключающееся в том, что электрическое поле в проводнике с током совершает работу, которая выделяется в виде тепла (нагревание проводников). И, наконец, химическое действие, заключающееся в выделении электрическим током в некоторых проводниках их составных химических частей.
Явление выделения током химических составных частей проводника получило название электролиза (от греческого лио — разлагаю). Электролиз имеет место не во всех проводниках. Проводники, в
которых не наблюдается химическое действие тока, называются
проводниками первого класса (рода). К их числу принадлежат все металлы, уголь и многие химические соединения. Проводники, в ко-
торых наблюдается химическое действие тока (в том числе и электролиз), называются проводниками второго класса (рода), а
электролитами — проводники, в которых происходит электролиз.
Электролитами являются многие водные растворы кислот и солей и некоторые химические соединения, как в жидком, так и в твердом состоянии.
Явление электролиза обычно осложняется вторичными реакциями. Вторичные реакции не связаны с наличием тока и не имеют прямого отношения к электролизу. Если, однако, отделить первичное действие тока от вторичных реакций, то можно обнаружить простое

6 Постоянный ток
правило: на отрицательном полюсе (катоде) всегда выделяются металлы и водород, а на положительном полюсе (аноде) — остаток химического coeдuнeнuя. При этом составные части электролита выделяются только на электродах, а в объёме электролита никакого выделения вещества не происходит.
Закон Ома
Если состояние проводника остаётся неизменным (не меняется температура и т.д.), то для каждого проводника существует зависимость между напряжением U (то же что и разность потенциалов), приложенным к концам проводника, и силой тока I в нём. Данная зависимость называется вольт-амперной характеристикой (ВАХ).
Для большинства проводников ВАХ носит линейный характер:
сила тока, текущего по однородному металлическому проводнику, пропорциональна напряжению U на проводнике:
I U |
(4а) |
|||
или |
|
|
|
|
I |
1 |
U. |
(4б) |
|
R |
||||
|
|
|
||
Зависимости (4а) и (4б) носят название закона Ома для однород-
ного участка цепи в интегральной форме в честь экспериментально
установившего его в 1826 году немецкого физика Георга Симона Ома или просто закона Ома. Ом имел дело только с однородными про-
водниками, т.е. проводниками, в которых действуют только электростатические силы (отсутствуют сторонние силы или ЭДС). В таких проводниках понятия напряжение и разность потенциалов полностью совпадают.
Коэффициент пропорциональности носит название электропроводности проводника, а величина, ей обратная — электрическо-
го сопротивления (R):
R1 .
Электрическое сопротивление проводников |
7 |
Единицей измерения электрического сопротивления R в системе СИ служит Ом: 1 Ом — сопротивление такого проводника, в котором течёт ток в 1 А, если к его концам приложено напряжение в 1 В (1Ом 1В 1А). Единицей измерения электропроводности служит Сименс, обратный Ому (1См 1Ом 1 ).
1А). Единицей измерения электропроводности служит Сименс, обратный Ому (1См 1Ом 1 ).
Электрическое сопротивление проводников
Электропроводность и сопротивление зависят от рода вещества проводника, от его геометрических размеров и формы, а также от состояния проводника. Если проводники состоят из однородного вещества, имеют форму цилиндров постоянного поперечного сечения, то в этом случае
R |
l |
, |
(5) |
|
S |
||||
|
|
|
где l — длина проводника, S — поперечное сечение проводника, а коэффициент пропорциональности зависит от рода вещества и от его состояния и называется удельным сопротивлением данного вещества. Единица измерения удельного сопротивления 1 Ом м или применяемая иногда (более удобная для практических расчетов) 1 Ом мм2/м. Величина, обратная удельному сопротивлению, получила название удельной электропроводности вещества ( ).
Как говорилось выше, удельное сопротивление а, следовательно, и сопротивление проводника зависят не только от рода вещества, но и от состояния данного вещества, в частности от температуры. Зависимость удельного сопротивления от температуры можно описать, задавая
температурный коэффициент сопротивления данного вещества:
|
1 |
|
d |
. |
(6) |
|
|
||||
|
dT |
|
|||
Температурный коэффициент сопротивления даёт относи-
тельное приращение удельного сопротивления (или просто сопротивления) при увеличении температуры на один градус.
Температурный коэффициент сопротивления для данного вещества различен при разных температурах. Это показывает, что
8 Постоянный ток
удельное сопротивление изменяется с температурой не по линейному закону, а зависит от неё более сложным образом. Однако для многих проводников, к которым относятся все металлы, изменение с температурой не очень велико. Если, к тому же интервал изменения температуры достаточно мал, то приближённо можно считать постоянным, равным среднему его значению внутри рассматриваемой области температур:
(t) 0(1 t). |
(7) |
где — удельное сопротивление при температуре t. Для однородных проводников аналогичная формула будет справедлива и для величины сопротивления:
R(t) R0(1 t). |
(8) |
Для интервалов температур включающих 0 С, при выражении температуры в градусах Цельсия, 0 и R0 в (7) и (8) имеют смысл удельного сопротивления и просто сопротивления при 0 С.
Для интервалов температур не включающих в себя 0 С, если 0 (R0 ) есть удельное сопротивление (сопротивление) при T0 формулы
(7)и (8) можно представить в другом виде:
(T) 0(1 (T T0));
R(T) R0(1 (T T0)).
Температурный коэффициент сопротивления может быть как положительным, так и отрицательным. У всех металлов сопротивление увеличивается с увеличением температуры, а следовательно, для металлов 0. Для многих других проводников первого класса наблюдается обратное и, по крайней мере в некотором температурном интервале, их сопротивление уменьшается с увеличением температуры. Наконец, у всех электролитов (проводники второго класса), сопротивление при нагревании всегда уменьшается и для них также 0.
Последовательное и параллельное соединение проводников |
9 |
Последовательное и параллельное соединение проводников
Если несколько проводников (резисторов, сопротивлений) соединены последовательно, то их можно рассматривать как один проводник с сопротивлением, рассчитываемым по формуле:
Rобщ R1 R2 , |
(9) |
где R1, R2, — сопротивления проводников. Формула (9) легко получается из закона Ома для участка цепи. Заметим, что разность потенциалов на всех проводниках складывается из разности потенциалов на каждом из них, тогда, переходя к напряжениям, можно написать:
Uобщ U1 U2 ,
где U1, U2, — падения напряжения на каждом проводнике, а Uобщ — падение напряжения на всех проводниках. Из закона Ома получаем U RI. Если нигде в рассматриваемой цепи не происходит накапливания электрического заряда, то согласно закону сохранения заряда, через сопротивления проходит одинаковый заряд за одно и тоже время. Тогда ток, проходящий через все проводники одинаков. Получаем
IRобщ IR1 IR2
или, после сокращения на силу тока I, формулу (9).
В случае параллельного соединения проводников будет одинаковым разность потенциалов на концах проводников, т.к. разность потенциалов берётся между одними и теми же точками (падением потенциала в проводах пренебрегаем). Количество заряда, проходящего через проводники за единицу времени будет равно сумме зарядов, проходящих через каждый проводник. Тогда полный ток через данную цепь будет равен сумме токов через каждый проводник (резистор):
|
U |
|
U |
|
1 |
|
1 |
|
|
|
|
||||
I I1 I2 |
|
|
|
U |
|
|
|
|
|
|
|
||||
|
R1 |
|
R2 |
|
|
|
R2 |
|
|
R1 |
|
||||
С другой стороны, сила тока на всем участке равна Rобщ — общее сопротивление цепи. Следовательно,
.
I U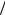 Rобщ , где
Rобщ , где

10 Постоянный ток
1 |
|
1 |
|
1 |
. |
(10) |
|
R |
R |
R |
|||||
|
|
|
|
||||
общ |
|
1 |
|
2 |
|
|
Для частного случая двух сопротивлений формулу (10) можно представить в более удобном виде:
R |
|
R1R2 |
. |
|
|
||||
общ |
|
R R |
||
|
|
1 |
2 |
|
Следует иметь ввиду, что полученные формулы справедливы только для однородных участков цепи, так как при их выводе использовалось определение напряжения для однородного участка цепи.
Закон Ома в дифференциальной форме
Найдем связь между векторами j |
и E в |
|
|
dl |
|
некоторой точке проводника. Выделим мыслен- |
|
|
|
j |
|
|
|
|
|||
но в окрестности этой точки элементарный ци- |
|
|
|
||
dS |
|
E |
|||
линдрический объём (рис. 1) с образующими |
|
|
|
||
длиной dl, параллельными векторам j |
и E . |
|
|
|
|
|
|
Рис. 1 |
|||
Через поперечное сечение цилиндра dS течёт
ток силой jdS. Напряжение, приложенное к цилиндру, равно Edl, где Е — напряжённость поля в данном месте. Наконец, сопротивление
цилиндра, согласно формуле (5), равно dl dS . |
Подставив эти зна- |
||
чения в закон Ома (4), придём к соотношению |
|
||
jdS |
dS |
Edl. |
(11) |
|
|||
|
dl |
|
|
Сократив dS и dl, а, также воспользовавшись тем, что векторы j и E имеют одинаковое направление для изотропного проводника, можно написать
j E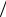
или в общепринятом виде:
j E. |
(12) |
Эта формула выражает закон Ома для однородного участка цепи в дифференциальной форме.
