Упражнение 3. Метод Ньютона (метод касательных).

Пусть задано уравнение вида , которое вблизи некоторой точкиимеет корень, при котором.

Пусть график этой функции имеет вид, показанный на рисунке 3.

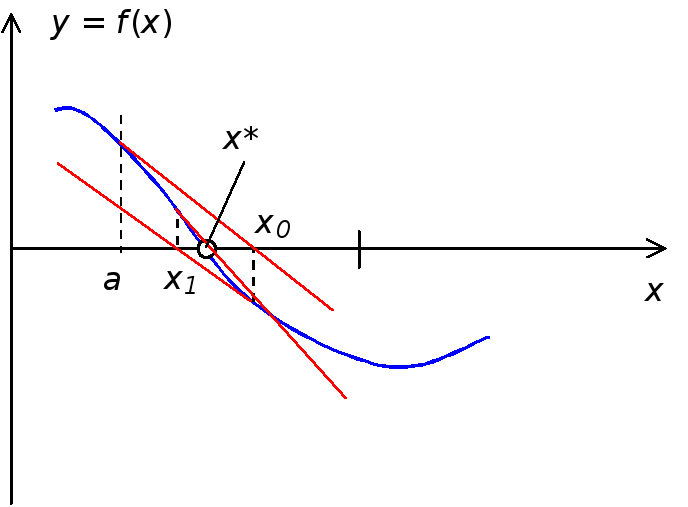
Рисунок 3

В точке проводится касательная к графику функции, которая пересекает осьв точке. Из определения производной функции в точке:

находим значение :

.

В точке проводится касательная к графику функции, которая пересекает осьв точке:

Подобный процесс выполняется до тех пор, пока где—-ое приближение к корню;— наперед заданное малое число.

Общая формула выбора приближения для метода Ньютона имеет вид:

На каждом шаге итерации производная определяется следующим образом:

где — малое число.

Алгоритм метода Ньютона в среде MathCad выглядит следующим образом:

При помощи функции Tangent (a, ) найдите корень заданной функции с точностью 10^–6:

Значение начального приближения должно быть задано в начале программы.

Измените функцию Tangent (a, ) таким образом, чтобы она могла подсчитать число итераций необходимых для поиска корня с заданной точностью (для этого создайте целочисленный параметрв начале функций, который затем при каждой итерации увеличивается на единицу).

Результаты расчетов должны быть сведены в таблицу:

Функция из варианта задания ______________________________
Метод	Корень	Число итераций
Метод бисекции
Метод хорд
Метод Ньютона

Сделайте вывод о том, какой из изученных методов является наиболее быстродействующим, позволяющим за меньшее число итераций определить корень уравнения с заданной точностью. Укажите недостатки рассмотренных методов.

Контрольные вопросы

1. Метод бисекции: суть метода, его достоинства и недостатки.

2. Метод хорд: суть метода, его достоинства и недостатки.

3. Метод Ньютона: суть метода, его достоинства и недостатки.

4. Сравнение различных методов расчёта корней трансцендентных уравнений.

Литература

1. Самарский А.А. Введение в численные методы. — М.: Наука, 1988.

2. Анго А. Математика для электро- и радиоинженеров. — М.: Наука, 1967.

ЛАБОРАТОРНАЯ РАБОТА №3

Расчет дисперсионных характеристик плоского трехслойного оптического волновода в программе MathCad

ЦЕЛЬ РАБОТЫ: получение навыков расчета дисперсионных характеристик мод плоского трехслойного оптического волновода на основе численных методов поиска корней в программном пакете MathCad.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Дисперсионное уравнение для волноводных мод плоского трехслойного диэлектрического волновода. Подход геометрической оптики.

В лабораторной работе изучается методика расчета дисперсионных характеристик плоского трехслойного диэлектрического оптического волновода (световод показан на рисунке 1).

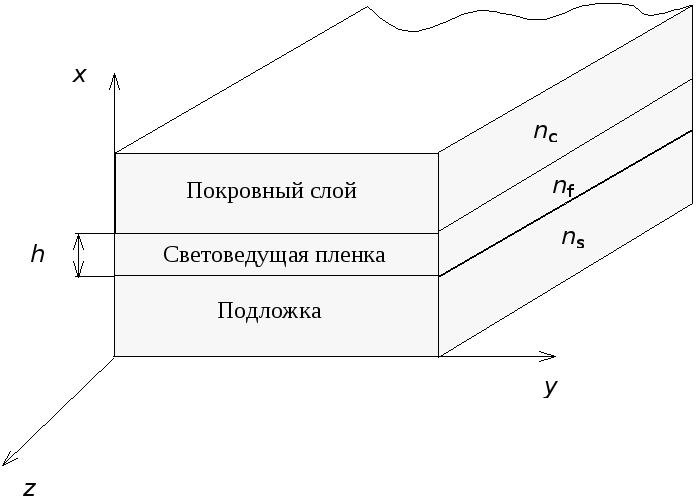
Рисунок 1

Рассматриваемая структура состоит из трех диэлектрических слоев: волноведущей пленки с показателем преломления, покровного слоя () и подложки (). Для устранения межмодовой дисперсии пленка может иметь плавно изменяющийся показатель преломления. Согласно лучевой теории, в этом случае различные моды, имеющие неодинаковые фазовые скорости будут испытывать различные по величине рефракционные искривления траектории луча. Для возможности канализации излучения в центральном слое необходимо выполнение условия:. В этом случае световая волна будет распространяться вдоль волноведущей пленки путем переотражений от границ раздела «пленка-покровный слой» и «пленка-подложка», где будет выполняться условие полного внутреннего отражения. Различные углы переотражений будут соответствовать различным типам собственных волн (модам). При этом необходимо выполнение условия фазового согласования:

(1)

где — толщина волноведущей пленки,— угол переотражения,— сдвиги фаз при отражении световой волны от покровного слоя и подложки соответственно,— индекс, определяющий порядковый номер моды.

В формуле (1):

— сдвиги фаз при отражении от границ раздела «пленка-покровный слой» и «пленка-подложка».

Из приведенного соотношения следует вывод, что в рассматриваемой световедущей структуре возможно распространение бесконечного числа мод, обладающих дискретными углами переотражения .

В интегральной оптике принято при построении дисперсионных характеристик переходить к безразмерным нормированным величинам, аналогам волнового числа и постоянной распространения(— волновое число для вакуума). Обычно используют три нормированных параметра:

—эффективный волноводный показатель преломления;

—нормированная частота;

—нормированный эффективный волноводный показатель преломления.

Для описания степени асимметрии показателей преломления подложки и покровного слоя вводят параметр асимметрии:

. (2)

При () оптический волновод называетсясимметричным; при () —несимметричным.

В результате введения нормированных параметров дисперсионное уравнение для плоского трехслойного оптического волновода (1) для случая постоянного показателя преломления волноведущей пленки имеет вид:

(3)

Частоты отсечек такого волновода определяются из соотношения:

(4)

ВАРИАНТЫ ЗАДАНИЙ:

№	Nf	Nc	Ns	Порядок моды
1	4.0	1.0	1.0	0, 1, 2
2	4.0	2.0	1.5	0, 1, 2
3	4.0	1.5	2.0	0, 1, 2
4	4.0	1.7	2.3	0, 1, 2
5	4.0	2.2	1.0	0, 1, 2
6	3.0	2.2	2.0	0, 1, 2

В таблице Nf — показатель преломления в середине световедущей пленки; Nc — показатель преломления покровного слоя; Ns — показатель преломления подложки.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ: