1. Метод подобия

2. Применение метода подобия в задачах математической физики

Многие методы решения задач математической физики применимы только к таким процессам, которые описываются с достаточной точностью линейными дифференциальными уравнениями. Круг таких задач весьма ограничен. В большинстве важных практических задачах, возникающих в физике и особенно в прикладных, инженерных дисциплинах, для получения результатов на требуемом уровне точности необходимо учитывать множество различных факторов.

Прежде всего, возрастает число физических параметров, которые необходимо учитывать и которые оказывают заметное влияние на исследуемый процесс. Уже это усложняет исследование процесса и проведение численного моделирования. Кроме того, попытки линеаризации уравнений часто приводят к неприемлемо большим погрешностям, а зачастую и к неверным физическим выводам. Следовательно, для уточнения результатов решения задачи необходимо в уравнения вводить нелинейные члены, например, учитывать зависимость коэффициентов теплопроводности от температуры.

В настоящее время не существует общей теории решения нелинейных задач. В то же время разработаны различные методы, позволяющие упростить исследование физических процессов, а также провести предварительный качественный анализ и зачастую получить с вполне приемлемой точностью требуемые результаты.

Большинство этих методов основывается на сложном современном математическом аппарате (методы современной геометрии, алгебры и математического анализа, например теории непрерывных групп). Поэтому рассмотрим один из широко распространенных и весьма эффективных методов, нашедших широкое применение во многих отраслях знания, и в то же время сравнительно простой метод подобия, основанный на анализе размерностей физических величин задачи. В математике этот метод обосновывается в так называемой теории размерностей.

1.2. Математические основы метода подобия

Любой реальный процесс описывается некоторым конечным набором физических величин, например силой, плотностью, скоростью и т.д. Обозначим этот набор величин x₁,…,x_m. Эти величины выражаются через некоторые независимые фундаментальные физические величины, такие как длина, время, масса, заряд и т.д. Пусть z₁,…,z_γ обозначают эти величины. Так как выбор численных значений фундаментальных величин произволен (определяется некоторыми соглашениями, эталонами), существуют масштабные множители λ=(λ₁,…,λ_γ) – положительные действительные числа, с помощью которых осуществляется преобразование эталонных

,

а, следовательно, измеряемых физических величин

исследуемого процесса, где показатели степени α_ij, i=1,…,r, j=1,…,m, определяются физической зависимостью величины x_j от фундаментальных единиц z_i.

В качестве примера рассмотрим следующую задачу. Пусть некоторый физический процесс описывается такими независимыми величинами, как скорость ν движения тела и плотность ρ жидкости. Размерность скорости – отношение длины (λ₁) ко времени (λ₂), а размерность плотности – отношение массы (λ₃) к объему, т.е. к кубу длины. Тогда

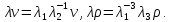
Если некоторая величина остается неизменной при данных преобразованиях, то она называется безразмерной.

Вообще говоря, между физическими величинами в любом реальном процессе возникают некоторые функциональные соотношения вида

Например, для поверхностных волн в глубокой воде скорость ν является функцией от длины волны l и гравитационной постоянной ускорения g. Такое соотношение называется масштабно инвариантным, если оно не меняется при изменении масштабов измерения основных величин. Оказывается, существует возможность выразить всякое такое соотношение только через безразмерные комбинации физических величин. Например, в рассмотренном примере, если λ=(λ₁,λ₂) – коэффициенты преобразования длины и времени, соответственно, то

.

Единственная безразмерная величина здесь – это число Фруда или его степень. Таким образом, всякое масштабно-инвариантное соотношение, определяющее скорость волны как функцию от длины волны и гравитационного ускорения, должно иметь вид

,

где постоянную c определяют из эксперимента.

Рассмотренный пример сравнительно легкий для того, чтобы простым подбором без привлечения специального математического аппарата установить ту безразмерную величину, которая определяет масштабно-инвариантное соотношение задачи. В более сложных задачах при наличии большого числа физических величин, влияющих на результат, установлению такого соотношения помогает метод подобия, в основе которого лежит так называемая π-теорема. Эта теорема – основа теории размерностей математического аппарата метода подобия. Приведем ее полную формулировку.

π-теорема.

Пусть z₁,…,z_γ – фундаментальные физические величины, масштабы измерений которых меняются независимо:

.

Пусть x₁,…,x_m – производные величины, изменяющиеся в соответствии с формулой

(1)

,

где A=(α_ij) – матрица размера r×m, элементы которой – константы. Пусть s– ранг матрицы A. Тогда существует m-s независимых безразмерных величин вида

(2)

обладающих тем свойством, что всякая другая безразмерная величина может быть записана как функция от π_1,…,π_m-s. Показатели степени β_ik в (2) являются m-s линейно-независимыми решениями линейной системы алгебраических уравнений

(3)

Если – произвольное масштабно-инвариантное соотношение на данные производные величины, то существует эквивалентное соотношение, которое может быть выражено только через указанные безразмерные величины:

(4)

Доказательство этой теоремы опирается на аппарат теории непрерывных групп.