
34-50_Elektrotekhnika
.pdf
Таблица2.2
I1′ I2′ I3′ I1′′ I2′′ I3′′ I1′′′ I2′′′ I3′′′ I1 I2 I3
A A A A A A A A A A A A
Измерено
Вычислено
Экспериментальная проверка метода эквивалентного генератора
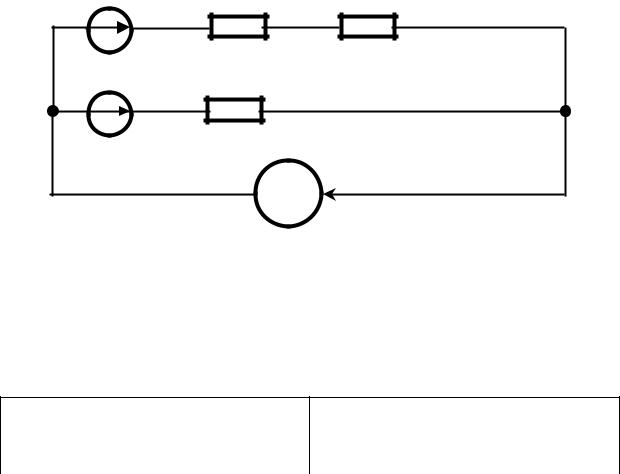
2.4.10.Для определения тока в ветви с источником Е3 методом эквивалентного генератора, собрать схему электрической цепи в соответствии с рис.2.5.
2.4.11.Значения ЭДС источников электрической энергии установить
Е1=12В, Е2=14В.
2.4.12.Произвести отсчет показания табло вольтметра РU, соответст-
вующее Э.Д.С.-ЕГ=UХХ эквивалентного генератора. Измеренное значение занести в таблицу 2.3.
E1 |
R18 |
R10 |
|
||
E2 |
R13 |
|
|
|
UXX |
|
|
РU |
Рис. 2.11
2.4.13.Для определения тока короткого замыкания IКЗ собрать схему электрической цепи в соответствии с рис.2.6.
2.4.14. Произвести отсчет показания табло амперметра РА соответствующее току короткого замыкания IКЗ на зажимах эквивалентного генератора. Измеренное значение занести в таблицу 2.3
3 1
E1 |
R18 |
|
R10 |
|
|
||
E2 |
R13 |
|
|
|
|
РA |
IКЗ |
|
|
|
Рис.2.12
Таблица 2.3
ИЗМЕРЕНО ВЫЧИСЛЕНО
UXX=EГ |
IКЗ |
RГ=Uхх/Iкз |
I3 |
|
|
|
|
2.5ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
2.5.1Вычислить аналитически, используя метод уравнений Кирхгофа, токи в ветвях схемы и напряжения на элементах цепи. Занести полученные значения в таблицу и сравнить с измеренными в опыте п.2.4.5, п.2.4.6. По полученным данным проверить справедливость законов Кирхгофа для исследуемой цепи.
2.5.2Вычислить аналитически потенциалы точек для схемы опыта п. 2.4.6, занести их в таблицу 2.1 и сравнить с потенциалами, измеренными в этом опыте.
2.5.3По данным опыта п..2.4.6 построить потенциальную диаграмму
для контура |
1-2-3-4-5-1. |
2.5.4 По данным опыта п. 2.4.9 вычислить токи в ветвях электрической
цепи I1=I11+I21+I31 ,I2=I12+I22+I32 ,I3=I13+I23+I33.Сравнить получен-
ные значения токов с данными опыта п. 2.4.5 2.5.5 Вычислить аналитически токи для схем представленных на
рис.2.2, рис.2.3, рис.2.4, занести полученные значения в таблицу 2.2 и сравнить данные величины с токами ,измеренными в опыте 2.4.5.
3 2
2.5.6По данным опыта п2.4.5 и выполненным вычислениям проверить справедливость метода наложения.
2.5.7По результатам измерений выполненных в п.2.4.12-2.4.14 определить ток I3 .Результаты занести в таблицу 2.3.
2.5.8Используя программу схемотехнического моделирования выполнить виртуальный эксперимент, для чего необходимо выполнить графический ввод исследуемых схем и определить значения измеряемых параметров Сравнить результаты схемотехнического моделирования с экспериментально полученными данными. Сделать вывод о сходимости результатов
2.5.9Составить баланс мощностей для схемы рис.2.1.Сравнить активные мощности, отдаваемые источниками, с активными мощностями, потребляемыми резисторами.
2.6 КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ ЗАЩИТЫ
Для защиты лабораторной работы необходимо выполнить компьютерное тестирование по теме “Методы расчета цепей постоянного тока”
2.7СОДЕРЖАНИЕ ОТЧЕТА
•Схемы исследуемых цепей
•Таблицы экспериментальных и расчетных данных
•Результаты цифрового моделирования исследуемых схем
•Потенциальные диаграммы ,полученные экспериментально и на основании расчетных данных
3 3
3. Лабораторная работа №3
Исследование линейных цепей переменного тока в установившемся режиме
3.1 ЦЕЛЬ РАБОТЫ
Цель работы: исследование основных свойств линейных электрических цепей с гармоническими (синусоидальными) источниками ЭДС, применяя на практике метод комплексных амплитуд.
3.2 ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ
Для решения основных задач анализа гармонических колебаний в линейных электрических цепях преимущественно используется метод, основанный на замене операций над синусоидальными функциями, описывающими колебания, операциями над комплексными числами, содержащими полную информацию о параметрах колебаний. Возможность подобной замены обусловлена тем, что в режиме гармонических колебаний все колебания имеют одну и ту же заранее известную частоту. Тогда функция U (t ) = U m sin( ωt + ψ ) , описывающая гармоническое колебание известной
частоты, характеризуется лишь двумя вещественными числами:
-амплитудой - U m
-и начальной фазой - ψ (рис.3.1.а).
Эти два числа можно объединить в одно комплексное число
•
U m =U m e jψ (рис.3.1.б), которое может рассматриваться как символическое изображение синусоидальной функции.
3 4

U(t) |
|
+j |
|
|
|
• |
|
2π |
|
Um |
|
|
|
|
|
|
Um |
|
|
|
|
Ψ |
|
Ψ |
ωt |
|
+1 |
|
|
|
|
а) |
рис.3.1 |
б) |
|
|
|
|
|
• |
• |
|
|
Комплексное число (U m =Um e jψu ; I m = Im e jψi ) , модуль которого равен |
|
||
амплитуде, а аргумент – начальной фазе функции, описывающей |
|
||
гармоническое колебание [u(t) =Um sin(ϖt +ψu );i(t) = Im sin(ϖt +ψi )] , называться |
|||
комплексной амплитудой колебания (напряжения, тока). Для комплексных амплитуд колебаний формально верны законы Кирхгофа и Ома, поэтому при анализе электрических цепей можно применять все методы, правила и формулы, используемые при анализе резистивных электрических цепей.
Отличие будет заключаться лишь в том, что вместо терминов «напряжение», «ток», «сопротивление», «проводимость» используются термины «комплексная амплитуда напряжения», «комплексная амплитуда тока», «комплексное сопротивление», «комплексная проводимость»
элементов (ветвей) цепи.
Комплексным сопротивлением Z ( jω) двухполюсника (комплексом полного сопротивления) называется отношение комплексных амплитуд напряжения и тока на входе двухполюсника. Схемное обозначение двухполюсника приведено на рис. 3.2.а.
3 5

I• |
|
|
|
R |
|
• |
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
Z( jω) • |
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
• |
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
б) |
|
|
|
|
R |
• |
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
• |
|
|
|
|
• |
|
|
• |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
I1 |
|
|
|
|
I 2 |
|
|
I 3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
• |
|
|
С |
|
|
|
• |
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
U |
|
|
R1 |
|
|
|
L |
|
|
C |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис.3.2 |
|
|
|
|
|
|
г) |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В соответствии с определением Z (iω) = |
Um |
= |
1 |
|
, где Y ( jω) - комплекс- |
||||||||||||||||
• |
Y ( jω) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ная проводимость (комплекс полной проводимости) двухполюсника.
|
|
|
|
|
• |
• |
Для |
упрощения |
обозначений вместо комплексных амплитуд колебаний |
Um и |
Im |
||
принято |
составлять уравнения для комплексных действующих |
значений |
||||
• |
|
• |
• |
• |
|
|
U |
=Um |
2 ; I = |
Im 2 . |
|
|
|
В простейших случаях, когда двухполюсник представляет собой пассивный элемент электрической цепи, коэффициенты, связывающие между со-
3 6

бой комплексные действующие значения напряжений и токов, определяется как:
•
Z L ( jω) = U•L = jωL = jX L ; X L =ωL ; IL
ZR ( jω) = R ;
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
Z |
C |
( jω) = |
UC |
= |
1 |
= − j |
1 |
= − jX |
C |
; |
X |
C |
= |
1 |
; |
|
jωC |
ωC |
ωC |
||||||||||||
|
|
• |
|
|
|
|
|
|
|||||||
|
|
|
IC |
|
|
|
|
|
|
|
|
|
|
|
|
и являются комплексными сопротивлениями, соответственно, индуктивности, резистив-ного сопротивления и емкости.
Коэффициенты обратные к приведенным выше:
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Y ( jω) = |
|
I L |
|
= |
|
1 |
= − jB |
|
; B |
|
= |
|
1 |
; |
||||||
|
|
|
|
|
|
jωL |
|
|
ωL |
|||||||||||
L |
|
• |
|
|
|
|
|
L |
|
L |
|
|
||||||||
|
|
|
U L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
YR (Jω) = |
|
IR |
= |
|
1 |
= G ; |
|
|
|
|
|
|
|
|||||||
|
• |
|
|
|
|
|
|
|
|
|
||||||||||
|
UR |
|
|
|
R |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Y (Jω) = |
|
IC |
|
= jωC = jB ; |
|
B = ωС |
|
|||||||||||||
|
|
|
|
|||||||||||||||||
C |
|
• |
|
|
|
|
|
|
C |
|
С |
|
|
|
|
|
||||
UC
-являются комплексными проводимостями соответствующих элементов.
Комплексное сопротивление и комплексная проводимость двухполюсника при произвольном соединении элементов, входящих в его состав, соответственно, равны:
Z ( jω) = Rϑ + jXϑ ; Y ( jω) =Gϑ = jBϑ ,
где Rϑ и Gϑ - эквивалентные активные составляющие, соответственно,
комплексного сопротивления и комплексной проводимости двухполюсника;
Xϑ и Bϑ - эквивалентные реактивные составляющие, соответственно, комплексного сопротивления и комплексной проводимости двухполюсника.
3 7

Используя показательную форму записи комплексных чисел можно записать:
Z( jω) =| Z( jω) | eJγZ ; Y ( jω) =|Y ( jω) | eJγY ;
| Z( jω) |=  Rϑ2 + Xϑ2 ; |Y ( jω) |=
Rϑ2 + Xϑ2 ; |Y ( jω) |=  Gϑ2 + Bϑ2 ,
Gϑ2 + Bϑ2 ,
где | Z ( jω) | и |Y ( jω) | - модуль, соответственно, комплексного сопротивления и комплексной проводимости двухполюсника (в дальнейшем для модулей сопротивлений и проводимостей будут использоваться также и сокращенные обозначения | Z | и |Y |);
γZ и γY - аргументы, соответственно, комплексного сопротивления и комплексной проводимости двухполюсника.
Так как | Z | eJγ Z =| Z | cosγZ + J | Z | sinγZ , |
а |Y | eJγY =|Y | cosγY + J |Y | sinγY , то в этих |
||
выражениях: |
|
|
|
Rϑ =| Z | cosγZ |
= Re Z ( jω) ; |
Xϑ =| Z | sinγZ = JmZ ( jω) ; |
|
Gϑ =| Y | cosγY |
= ReY ( jω) ; |
Bϑ =| Y | sinγY |
= JmY ( jω) . |
Рассмотрим ряд простейших примеров, иллюстрирующих вычисление и преобразование комплексных сопротивлений и проводимостей двухполюсников. На рис.3.2.б приведена схема двухполюсника, содержащего индуктивность и резистивное сопротивление, соединенные последовательно. Так как при последовательном соединении двух-полюсников их сопротивления суммируются, то комплексное сопротивление рассматриваемого двухполюсника, при записи в алгебраической форме, будет таким:
Z ( jω) = R + JωL , где активная и реактивная составляющие, соответственно, равны Rϑ = R , а Xϑ =ωL .
Модуль сопротивления двухполюсника равен модулю Z ( jω) , т.е. R2 + (ωL)2 , а аргумент γZ = arctgωL /R; поэтому в показательной форме записи
Z ( jω) = R2 + (ωL)2 e jγ Z .
Комплексная проводимость рассматриваемого двухполюсника такова:
Y (Jω) = |
1 |
= |
1 |
. |
|
Z (Jω) |
R + jωL |
||||
|
|
|
3 8

Чтобы представить Y (Jω) в алгебраической форме, следует числитель и знаменатель Y (Jω) умножить на комплексную величину, сопряженную со знаменателем, тогда
Y (Jω) = |
R − jωL |
= |
|
R |
− |
|
jωL |
, где |
Gϑ = |
|
R |
, |
||
(R + jωL)(R − jωL) |
|
R2 +(ωL)2 |
R2 |
+(ωL)2 |
R2 |
+(ωL)2 |
||||||||
|
|
|
|
|
|
|
|
|||||||
а Bϑ = |
|
ωL |
. В показательной форме записи |
|
|
|
|
|||||||
R2 +(ωL)2 |
|
|
|
|
||||||||||
Y ( jω) =|Y | eJγY = |
1 |
|
|
e− jarctgωL R . |
|
|
|
|
|
|
|
|||
|
|
|
R2 +(ωL)2 |
|
|
|
|
|
|
|
|
|
||
Значит |Y ( jω) |= |
1 |
|
|
; |
γY = −arctgω L R . |
|
|
|
|
|||||
R2 +(ωL)2 |
|
|
|
|
||||||||||
Для двухполюсника из последовательно соединенных резистивного и емкостного элемен-
тов(рис.3.2в) аналогичнонаходим Z ( jω) = R + |
1 |
|
|
= R − j |
1 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
jωC |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
|||||
Следовательно, X |
ϑ |
= |
|
|
1 |
|
; |
| Z( jω) |= |
R2 + |
|
1 |
; |
|
γ |
Z |
|
= arctg(− |
|
1 |
|
) = −arctg |
1 |
; |
||||||||||||||||||||
|
|
|
|
ω2C2 |
|
ωCR |
ωCR |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Y ( jω) = |
|
1 |
|
|
|
= |
|
|
|
jωC |
|
|
|
|
|
. В |
последнем |
|
выражении |
|
|
|
|
|
jωC =ωCe jπ 2 |
и |
|||||||||||||||||
|
1 |
|
|
1 |
+ jωCR |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
R + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
jωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 + (ωCR)2 |
e jarctgωCR , поэтому Y ( jω) = |
|
|
|
|
ωC |
e j( |
π |
−arctgωCR) , азначит |
|||||||||||||||||||||||||||||
1 + jωCR = |
|
|
|
|
2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+(ωCR)2 |
|
|
|
|
|
|
|
|
|
|||||
|Y ( jω) |= |
|
ωC |
|
|
|
; |
|
γY |
= |
π |
|
− arctgωCR . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
1 +(ωCR)2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Наконец |
Y (Jω) |
= |
|
|
|
jωC |
|
|
|
= |
|
jωC(1− jωCR) |
|
|
|
= |
|
|
ω2C 2 R |
|
+ |
|
|
|
jωC |
; |
|
|
|||||||||||||||
1+ jωCR |
|
(1+ jωCR)(1− jωCR) |
1 |
+(ωCR)2 |
1 |
+(ωCR)2 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Gϑ = |
|
|
ω2C 2 R |
|
|
|
и |
|
|
|
Bϑ = |
|
|
|
|
|
ωC |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
+(ωCR)2 |
|
|
|
|
|
1 |
+ |
(ωCR)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
На рис.3.2г приведена схема двухполюсника, содержащего три соединенные
параллельно ветви с комплексными проводимостями:
3 9

Y1( jω) = |
1 |
; |
Y2 ( jω) = |
|
|
1 |
; Y3 ( jω) = jωC . |
|
R |
R |
2 |
+ jϖL |
|||||
|
|
|
|
|||||
|
1 |
|
|
|
|
|
При параллельном соединении двухполюсников их комплексные проводимости суммируются, поэтому:
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
R2 |
jϖL |
|||
Y ( jω) = |
|
+ |
|
|
|
+ jωC , или Y ( jω) |
= |
|
+ |
|
|
|
+ jωC − |
|
|
. |
|||
R |
R |
2 |
+ jϖL |
R |
|
R2 |
+(ϖL)2 |
R2 |
+(ϖL)2 |
||||||||||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
2 |
2 |
|
|
|||
|
|
|
|
|
|
|
R1R2 + R22 +(ωL)2 |
|
|
Bϑ |
= |
ω3 L2C +ω(CR22 − L) |
|||||||
Следовательно, Gϑ = |
|
; |
|
|
R22 +ω2 L2 |
; |
|
||||||||||||
(R22 +ω2 L2 )R1 |
|
|
|
||||||||||||||||
|Y |= |
1 = G2 |
+ B2 |
; |
γ |
Y |
= −γ |
Z |
= arctg |
Bϑ |
. |
|
|
|||||||||||
|
| Z | |
2 |
2 |
|
|
|
|
Gϑ |
|||
|
|
|
|
|
|
|
|
|
|||
По закону Ома в комплексной форме:
|
• |
|
Ue jψu |
|
|
|
|
|
|
|
|
|
|
|
|
Z ( jω) = |
U |
|
U |
e |
j(ψ |
|
−ψ |
) |
=| Z | e |
jγ |
Z ; |
||||
• |
= |
Ie jψi |
= |
I |
|
u |
|
i |
|
|
|||||
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
Ie jψi |
|
|
|
|
|
|
|
|
|
|
|
|
Y ( jω) = |
I |
= |
= |
I |
e |
j(ψ |
i |
−ψ |
u |
) |
=|Y | e |
jγ y |
; |
||
• |
Ue jψu |
U |
|
|
|
|
|
||||||||
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γz =ψu −ψi ; γ y =ψi −ψu ; γ y = −γz .
Здесь U, I - действующие значения напряжения и тока, которые могут быть определены по показаниям вольтметра. При этом I может определяться косвенным путем через напряжение UR , измеряемое вольтметром на активном сопротивлении R, т.е. I=UR /R.
Для пассивных двухполюсников аргументы комплексных сопротивлений и
проводимостей могут изменяться от 0 до ±π |
2 |
, |
т.е. − |
π |
≤γz ≤ |
π |
и |
|||
|
π |
|
π . |
|
|
2 |
|
2 |
|
|
− |
≤γ y ≤ |
|
|
|
|
|
|
|
||
|
2 |
|
2 |
|
|
|
|
|
|
|
4 0
