Метод координат Введение в векторную алгебру

1.1. НАПРАВЛЕННЫЕ ОТРЕЗКИ

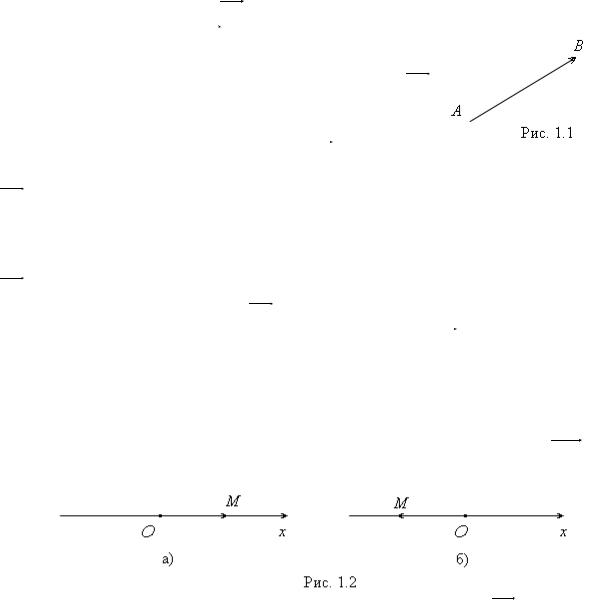
Определение 1.1. Упорядоченная пара точек

A и

B называется

направленным отрезком

АВ .

Первая точка

A

называется началом

направленного отрезка

АВ ,

а вторая точка B – его

концом (рис. 1.1).

В обозначении направленного

отрезка

АВ

порядок точек определяется порядком их записи:

A – первая точка, B – вторая. Если точки

A

и

B

различны, то направленный отрезок

АВ называется

ненулевым, а если точки

A

и

B

совпадают, то направленный отрезок

АВ

называется нулевым.

Определение 1.2. Осью называется прямая линия, на которой фикси-

ровано положительное направление и выбран масштабный отрезок.

Определение 1.3. Координатой ненулевого направленного отрезка

АВ ,

лежащего на оси

l , называется число

x ,

модуль которого равен

длине направленного отрезка

АВ , измеренной масштабным отрезком оси

l; оно положительно, если направленный отрезок

АВ

и ось l

имеют

одинаковое направление, и отрицательно в противном случае.

Определение 1.4. Осью координат называется ось, на которой фик-

сирована точка O , называемая началом координат.

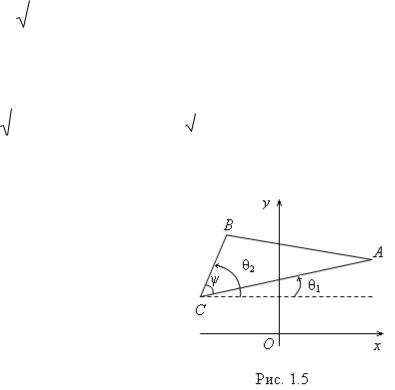
Определение 1.5. Координатой

x1

точки

M ,

лежащей на оси

координат, называется координата направленного отрезка

OM

(рис. 1.2, а, б).

x =

x2 −

x1.

ТЕОРЕМА 1.2. Расстояние

d

между точками A(x1 ) и B(x2 )

оси координат, вычисляется по формуле

d =

x2 −

x1

.

угол

π

в положительном направлении, т.е. в направлении, противопо-

2

Пусть

M – произвольная точка плоско-

сти, не лежащая ни на одной оси координат.

Опустим из точки

M

перпендикуляры на оси

координат. Обозначим точки пересечения с

осью

Ox –

M1 , а с осью

Oy – M 2 (рис. 1.3).

Точки М1 и М2 – ортогональные проекции точки

M на оси координат. Пусть

x – координата

точки

M1

на оси

Ox , а

y – координата точ-

ки

M 2

на оси

Oy .

называются декартовыми или прямоугольными

Числа

x

и

y

координатами точки

M .

Первая координата

x – абсцисса точки M ,

вторая координата y – ордината точки

M .

x , y обознача-

Точка M

с координатами

ется

M (x; y) .

При помощи прямоугольной систе-

мы координат на плоскости устанавливается взаим-

но однозначное соответствие между множеством

всех точек плоскости и множеством всех упорядо-

ченных пар чисел. Координатные оси разделяют

всю плоскость на четыре части (рис. 1.4), называе-

мые четвертями. Четверти нумеруются по опреде-

ленному правилу. Точки, лежащие в каждой из них,

характеризуются знаком своих координат. Ордина-

ты

точек, лежащих на оси

Ox ,

равны нулю ( y = 0). Абсциссы точек, ле-

жащих на оси

Oy ,

равны нулю

(x =

0) .

Вычисление расстояния между двумя точками

ТЕОРЕМА 1.3. Для любых точек

M1 (x1 ; y1 )

и M 2 (x2 ; y2 )

плоско-

сти расстояние d между ними определяется формулой

d =

(х2 - x1)2 + ( y2 -

y1)2

.

(1.1)

П р и м е р .

Определить расстояние

между

точками A( 3;8 ) и

B( − 5;14 ).

Р е ш е н и е . Воспользовавшись формулой (1.1), получим

d =

(- 5 - 3)2 + (14 - 8)2

=

= 10 .

64 + 36

Вычисление площади треугольника по координатам его вершин

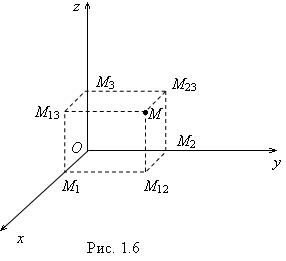
Пусть даны вершины треугольника

A(x1; y1) , B(x2 ; y2 ) ,

C(x3; y3 )

(рис. 1.5). Пусть

СА = d1 ,

СB = d2 и

ψ

–

S =

1 ×

d ×

d

2

× sinψ

.

2

1

Пусть

q 1 – угол между отрезком

CA и

осью Ox ,

q 2 – угол между отрезком

CB и

осью Ox . Так как

y

= q 2 - q 1 , то

1

× d1

× d2

× sinψ =

1 × d1 × d2 × sin(θ2 - θ1 ) =

2

1

2

=

× (d1 ×

cos θ1×

d2 × sinθ2 -

d2 × cos θ2 × d1 sinθ1 ).

2

x2 -

x1 =

d × cosθ , y2 - y1 = d × sinθ (эти формулы вы-

Учитывая, что

длину и угол между отрезком и осью

Ox ), получим, что

d1 × cosθ1 =

x1 -

x3 , d1 × sinθ1 =

y1 - y3 ,

d2 × cosθ2 =

x2 -

x3 , d2 × sinθ2 = y2 -

y3 .

Таким образом, выражение для площади треугольника имеет вид

S =

1 ×

(x -

x ) × ( y

2

-

y

3

) - (x

2

-

x ) × (y -

y

3

)

.

(1.2)

2

1

3

3

1

C лежит в начале координат

В частном случае, если вершина

(т.е. x3 = y3 = 0 ),

S =

± 1 × (x1 × y2 - x2 ×

y1) .

2

1 ×

1

1

1

S = ±

x1

x2

x3

.

2

y

y

2

y

3

1

П р и м е р .

Определить

площадь

треугольника с

вершинами

A(2;8) , B(10;2)

и

C(− 2;− 4) .

Р е ш е н и е .

Воспользовавшись формулой (1.2), получим

S = 1

(2 +

2)(2 + 4) - (10 +

2)(8 +

4)

= 1

24 - 144

=

60 (кв.ед.).

2

2

К осям абсцисс Ox и ординат

Oy

плоскости добавляется ось ап-

пликат – Oz . При этом положительное направление оси

Oz выбирается

таким образом, чтобы поворот от оси

Ox

к оси Oy

на угол, меньший

какой-нибудь точки положительной полуоси

Oz .

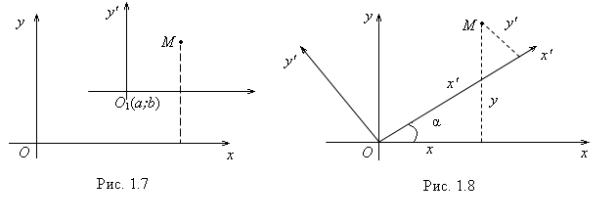
Пусть

M – произвольная точ-

ка пространства, а точки

M1 ,

M 2 ,

M3

– ортогональные проекции точки

M

на оси координат (рис. 1.6). Чис-

ла x = OM1 , y = OM2 и z = OM3 –

координаты точки

M

в заданной

прямоугольной

системе

координат.

Таким образом, точка в пространстве

задается тремя координатами

x,y,z

и записывается

M ( x; y;z) .

Три

координатные

плоскости

xOy , xOz

и

yOz

разделяют про-

O1 (a;b)

(рис. 1.7), связь между старыми и новыми координатами для не-

которой

точки

M

плоскости

определяется

формулами

x =

x′ +

a ,

y =

y′ +

b

(1.3)

или

y′ =

y −

b .

x′ =

x −

a ,

(1.4)

мость между старыми координатами

x, y

и новыми x′, y′

определяет-

ся следующими формулами:

x =

x′ cosα−

y′ sin α,

y =

x′ sinα+

y′ cosα.

(1.5)

или

x′ =

xcosα+

ysin α,

y′ =

− xsinα+

y cosα .

(1.6)

В случае пространства формулы перехода при параллельном перено-

се осей будут иметь следующий вид:

или

x = x′ +

a , y =

y′ + b ,

z = z′ +

c

(1.7)

x′ =

x − a , y′ =

y − b , z′ = z − c .

(1.8)

При повороте координатных осей

x =

x′ cos α1

+

y′ cos α2 +

z′ cos α3

ü

y = x¢ cos β1

+

y¢ cos β2 +

z¢ cos β3

ï

,

(1.9)

ý

z =

x¢ cos γ1 +

y¢ cos γ2 +

z¢ cos γ3

ï

þ

где α 1, α 2 , α 3

– углы, образуемые осью Ox

соответственно с новыми

осями Ox′ , Oy′ , Oz′ ;

β 1,β 2 ,β 3 , γ 1, γ 2 , γ 3 – углы, образуемые соответствен-

но осью

Oy и осью

Oz с новыми осями (или

α 1,β 1, γ 1 – образуемые но-

вой осью

Ox′

соответственно со старыми осями Ox , Oy , Oz и т. д.).

пользоваться полярной системой координат.

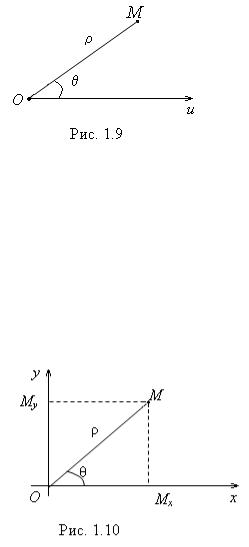
Полярная

система

координат (рис. 1.9)

определяется заданием некоторой точки

O ,

называемой полюсом, исходящего из этой точ-

ки луча, называемого полярной осью, и масшта-

ба для измерения длин.

M . Кроме

Возьмем на плоскости точку

задания полярной системы координат должно

быть указано положительное направление вра-

щения вокруг точки O (от полярной оси к лучу

OM

против часовой

стрелки). Число r =

OM

называется полярным радиусом и является пер-

вой координатой точки

M ,

а число θ – полярным углом и является вто-

рой координатой точки

M .

Определение 1.6. Полярный радиус и полярный угол точки называ-

ются полярными координатами.

Полярные координаты

ρ , θ записываются в скобках после буквы,

обозначающей точку: M (ρ ;θ ) .

M

Если точка

имеет полярные

координаты ρ >

0

и 0 ≤

θ <

2π , то ей же

отвечает и бесчисленное множество пар

полярных

координат

(ρ ,θ + 2kπ ) ,

где

k Z .

Выведем формулу перехода от по-

лярных координат к прямоугольным и

обратно.

Для

простоты

рассуждений

рассмотрим частный случай, когда полюс

полярной системы координат совпадает с

прямоугольные координаты точки

M ,

через ρ

и θ – ее полярные

координаты. Как известно,

x = OM x ,

y = OM y .

С другой стороны,

OM x = ρ× cos θ , OM y = ρ× sin θ .

Поэтому

x =

ρ× cos θ,

(1.10)

y =

ρ× sinθ.

Обратно, зная прямоугольные координаты точки, можно определить

ее полярные координаты по формулам

ρ =

x2 + y2 ,

(1.11)

tgθ =

y

.

x

1 . Найти полярные координаты точки M (1;-

).

3

Р е ш е н и е .

На основании равенств (1.11) находим

ρ =

12 + (-

= 2, tgθ = -

.

3)2

3

Очевидно, что точка

M лежит в IV четверти и, следовательно,

θ =

5π

3

.

Таким образом, полярные координаты точки

M (2;

5π

3

).

A(2

)

2. Найти прямоугольные координаты точки

,

заданной

2;3π

4

своими полярными координатами.

Р е ш е н и е .

На

основании

равенств

(1.10)

имеем

x =

2

cos(3π 4) =

- 2,

y = 2

sin(3π 4) =

2.

2

2

Таким образом, прямоугольные координаты точки

A(-

2;2) .

1.7. ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ

Пусть точка

M

имеет прямоугольные координаты

( x; y;z) .

Если

Q – ортогональная проекция точки

M

на плоскость

xOy ,

тогда ци-

линдрическими координатами точки

M

называются три числа (r ;q ; z) ,

где

(r ;q ) – полярные координаты точки Q( x; y)

в плоскости

xOy .

Заметим, что

ρ =

x2

+ y2

есть расстояние от точки

(0;0;z)

до

M (x; y;z) , т.е. расстояние от точки

M

до оси

Oz

(рис. 1.11).