2 курс ИНФОРМ ТЕХНОЛОГИИ ЖД ТРАНСП / 2 курс / Математика к. р. 2 курс
.pdfРОССИЙСКАЯ ОТКРЫТАЯ АКАДЕМИЯ ТРАНСПОРТА
________________________________________________________________
Одобрено кафедрой «Высшая и прикладная математика»
МАТЕМАТИКА
Задание на контрольные работы № 4-6 с методическими указаниями по выполнению
для студентов-бакалавров 2 курса направления: «Информационные системы и технологии»
профиля: «Информационные системы и технологии на транспорте»
Москва – 2012
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ
ОБЩИЕ УКАЗАНИЯ
Задачи, включенные в контрольную работу, взяты из сборника задач, подготовленного коллективом преподавателей кафедры «Высшая и прикладная математика» РОАТ МГУПС. Все задачи имеют тройную нумерацию, которая включает номер раздела из программы по математике для соответствующей специальности, уровень сложности задачи и порядковый номер задачи. Студент выполняет те задачи, последняя цифра которых совпадает с последней цифрой его учебного шифра. Например, студент, учебный шифр которого имеет последнюю цифру 1, в контрольной работе №4 решает задачи 15.1.61, 15.1.111, 15.2.61, 15.2.111, 15.3.11; в контрольной работе №5 – 11.2.11, 15.3.61, 16.1.11, 16.1.21, 16.2.1; в контрольной работе №6 – 17.1.11, 17.2.11, 17.2.31, 17.2.41, 17.3.11.
Перед выполнением контрольной работы студент должен ознакомиться с содержанием разделов математических дисциплин, на освоение которых ориентирована выполняемая контрольная работа. Необходимую учебную литературу студент может найти в рабочей программе по математике для своей специальности (в программе указана как основная, так и дополнительная литература).
Каждая контрольная работа выполняется в отдельной тетради, на обложке которой должны быть указаны: дисциплина, номер контрольной работы, шифр студента, курс, фамилия, имя и отчество студента. На обложке вверху справа указывается фамилия и инициалы преподавателя-рецензента. В конце работы студент ставит свою подпись и дату выполнения работы.
В каждой задаче надо полностью выписать ее условие. В том случае, когда несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
Решение каждой задачи должно содержать подробные вычисления, пояснения, ответ, а также, в случае необходимости, и рисунки. После каждой задачи следует оставлять место для замечаний преподавателя-рецензента. В случае невыполнения этих требований преподаватель возвращает работу для доработки без ее проверки.
2
|
|
|
|
|
КОНТРОЛЬНАЯ РАБОТА № 4 |
Обыкновенные дифференциальные уравнения и системы. |
|||||
15.1.61–15.1.70. Найти общее решение (общий интеграл) дифференциального уравнения. |
|||||
Сделать проверку. |
|
|
|
|
|
15.1.61. (х2 – у2)у' = 2ху; |
|
|
15.1.62. (1 + х2)у' – 2ху = (1 + х2)2; |
||
15.1.63. ху' = у1n(у/х); |
|
|
|
15.1.64. ху' + y = 3; |
|
15.1.65. ху' +хеy/х – y = 0; |
|
|
15.1.66. у'соs х – (у + 1)sinх; |
||
|
|
|
|
|
|
15.1.67. ху' – у = |
x 2 |
y |
2 |
|
2 |
|
|
; |
15.1.68. х у' – 2ху = 3; |
||
15.1.69. х2у' + у2 – 2xy = 0; |
15.1.70. ху' + у = x + 1. |
||||
15.1.111-15.1.120
15.1.111. Найти закон движения материальной точки массы m, если известно, что работа силы, действующей в направлении движения, пропорциональна пути от начала движения (коэффициент пропорциональности k).
15.1.112. Лодка пущена со скоростью 4 км/ч через реку и прибыла на другой берег со скоростью 2км/ч через 6 мин. Сила сопротивления воды пропорциональна квадрату скорости. Найти закон движения лодки и ширину реки.
15.1.113. У моторного судна при скорости 10 км/ч отключается мотор. Отрицательное ускорение, сообщаемое лодке сопротивлением воды, пропорционально скорости. Найти закон движения лодки.
15.1.114. Сила упругости, возникающая при растяжении пружины, пропорциональна увеличению ее длины и равна 1 Н, когда длина пружины увеличивается на 1 см. Найти закон движения груза, если его оттянуть книзу, а затем отпустить.
15.1.115. Кривая проходит через точку А(1; –2) и обладает тем свойством, что угловой коэффициент касательной в любой ее точке пропорционален квадрату ординаты точки касания с коэффициентом пропорциональности k = 2. Найти уравнение кривой.
15.1.116. Поезд, масса которого вместе с тепловозом равна M, движется прямолинейно. Сила тяги тепловоза постоянна и равна F. Сила f сопротивления движению поезда пропорциональна скорости движения. Найти закон движения поезда, если при t = 0, v = 0.
15.1.117. Локомотив массой М движется по некоторому участку пути со скоростью 60 км/ч. Через какой промежуток времени и на каком расстоянии от начала торможения он будет остановлен, если сила сопротивления движению при торможении равна 0,2 массы локомотива.
15.1.118. Вагоновожатый трамвая, включая реостат, постепенно увеличивает мощность двигателя так, что сила тяги возрастает от нуля пропорционально времени, увеличиваясь на 120
Нв секунду. Найти закон движения трамвая при следующих данных:
1)масса вагона 10 т;
3
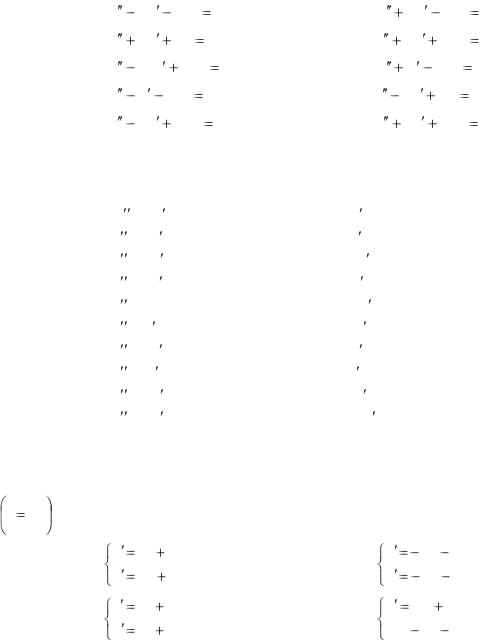
2)сопротивление трению постоянно и равно 200 Н;
3)начальная скорость равна нулю.
15.1.119. Материальная точка массой 2 г погружается в жидкость, сила сопротивления которой пропорциональна скорости погружения с коэффициентом пропорциональности k = 0,002 кг/с. Найти скорость точки через 1 с после начала погружения, если в начальный момент она была равна нулю.
15.1.120. Скорость химической реакции, при которой разлагается данное вещество, пропорциональна количеству неразложившегося вещества. Через час после начала реакции осталось 36 г неразложившегося вещества, а через 3 часа – 9 г. Сколько было взято вещества первоначально?
15.2.61–15.2.70. Найти общее решение линейного дифференциального уравнения.
Сделать проверку. |
|
|
|
|
|
|
|
|
|
15.2.61. |
y |
2 y |
15 y |
0 ; |
15.2.62. |
y |
2 y |
15 y |
0 ; |
15.2.63. |
y |
6 y |
9 y |
0 ; |
15.2.64. |
y |
6 y |
34 y |
0 ; |
15.2.65. |
y |
10 y |
34 y |
0 ; |
15.2.66. |
y |
y |
12 y |
0 ; |
15.2.67. |
y |
y |
12 y |
0 ; |
15.2.68. |
y |
6 y |
9 y |
0 ; |
15.2.69. |
y |
6 y |
25 y |
0 ; |
15.2.70. |
y |
8 y |
25 y |
0 . |
15.2.111–15.2.120. |
Найти |
частное |
|
решение |
линейного |
неоднородного |
||
дифференциального уравнения. Сделать проверку. |
|
|
|
|
||||
15.2.111. y |
– 3y |
– 4y = e-x, |
y(0) = 0, |
y (0) = –1; |
|
|
||
15.2.112. y |
– 6y |
+ 9y = x + 1, |
y(0) = 1, |
y (0) = 0; |
|
|
||
15.2.113. y |
+ 9y |
= x – 2 , |
y(0) = –2, |
y (0) = 1; |
|
|
||
15.2.114. y |
– 2y |
+ 10y = sin3x, |
y(0) =1, |
|
y (0) = 1; |
|
|
|
15.2.115. y |
+ 4y = x2, |
y(0) = –1, |
y (0) = 0; |
|
|
|||
15.2.116. y |
+ y |
– 6y = 2e-3x, |
y(0) = 0, |
|
y (0) = 2; |
|
|
|
15.2.117. y |
– 3y |
= cos2x, |
y(0) = 3, |
y (0) = 1; |
|
|
||
15.2.118. y |
– 4y |
+ 4y = 2sin3x, |
y(0) =0, |
y (0) = –1; |
|
|
||
15.2.119. y |
+ 4y |
+ 5y = 4ex, |
y(0) = 2, |
|
y (0) = 0; |
|
|
|
15.2.120. y |
+ 4y |
= cosx, |
y(0) = –2, |
y (0) = –1. |
|
|
||
15.3.11–15.3.20. Найти общее решение системы линейных дифференциальных уравнений с постоянными коэффициентами в матричной форме. Сделать проверку найденного решения
/ d |
|
|
|
||
|
|
. |
|
|
|
|
dt |
|
|
|
|
|
|
|
x |
4x |
6 y, |
15.3.11. |
y |
4x |
2 y. |
||
|
|
|
|||
|
|
|
x |
3x |
y, |
15.3.13. |
y 8x y. |
||||
|
|
|
|||
|
x |
5x |
4 y, |
15.3.12. |
y |
2x |
3y. |
|
|
|
x 6x 3y,
15.3.14.y
8x 5 y.
4
|
x |
x |
5 y, |
15.3.15. |
y |
x 3y. |
|
|
|
|
|
|
x |
4x |
6 y, |
15.3.17. |
y |
4x |
2 y. |
|
|
|
|
|
x |
x |
5 y, |
15.3.19. |
y |
7x |
3y. |
|
|
|
|
|
x 3x 2 y, |
15.3.16. |
y 2x 8 y. |
|
x 5x 8 y, 15.3.18. y
3x 3y.
x 7x 5 y,
15.3.20.y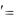
4x 8 y.
5
КОНТРОЛЬНАЯ РАБОТА № 5 Числовые ряды. Уравнения в частных производных.
Теория функций комплексного переменного.
11.2.11–11.2.20. Выяснить, какие из данных рядов сходятся и какие расходятся.
|
|
|
n |
2 |
|
. |
|
|
|
|
|
|||
11.2.11. n 1 n4 |
5 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
n |
|
|
|
|
|
||||
|
|
|
|
|
|
|
. |
|
|
|
|
|
||
11.2.13. n 1 n3 |
5 |
|
|
|
|
|
||||||||
|
|
|
n3 |
|
|
|
|
|
||||||
11.2.15. n 1 |
|
|
|
. |
|
|
|
|
|
|
||||
en |
|
|
|
|
|
|||||||||
|
|
|
|
3n |
2 |
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
11.2.17. |
n 1 |
|
|
n5n |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
1 |
n |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
11.2.19. n 1 |
3n |
2 |
|
|
||||||||||
|
|
|
||||||||||||
|
|
ln( n |
2) |
. |
|
11.2.12. |
n 1 |
n |
2 |
||
|
|||||
|
|
|
3n 11.2.14. n 1 (2n)!.
2 11.2.16. n 1 n ln 3 n.
n2 . 11.2.18. n 1 (3n)!
11.2.20. n 1 (nnn2)!.
15.3.61–15.3.70. |
Методом |
Даламбера |
найти уравнение |
u u(x;t) |
формы одной |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2u |
|
a2 |
2u |
|
|
|
бесконечной струны, определяемой волновым уравнением |
t 2 |
x2 , если в начальный |
||||||||||||||||||||||||
|
||||||||||||||||||||||||||
момент t0=0 форма |
струны и |
скорость |
|
точки |
струны |
с |
абсциссой x определяются |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
u |
|
|
|
f (x) и |
u |
|
|
F (x) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
t |
0 |
|
|
|
t 0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|||||||||||||||
соответственно заданными функциями |
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
15.3.61. f(х) = х(2 – х), |
|
|
F(x) = e-x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15.3.62. f(х) = х2, |
|
|
F(x) = sin x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15.3.63. f(х) = еx, |
|
|
F(x) = ωx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15.3.64. f(х) = cos х, |
|
|
F(х) = ωх. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15.3.65. f(х) = sin x, |
|
|
F(x) = v0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15.3.66. f(х)= х, |
|
|
F(x) = cos x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15.3.67. f(х) = sin x, |
|
|
F(x) = cos x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15.3.68. f(х) = x(x – 2), |
|
|
|
F(x) = ex. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
15.3.69. f(х) = cos x, |
|
|
F(x) = sin x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15.3.70. f(х) = e-x, |
|
|
F(x) = v0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
16.1.11–16.1.20. Найти значение функции w |
|
f (z) в точке z0 x0 iy0 . |
|
|||||||||||||||||||||||
f (z) |
2e z |
|
|
|
|
|
|
|
|
|
z |
0 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
16.1.11. |
|
|
|
|
|
|
2 ; |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
f (z) |
2 sin z |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
z0 |
|
i ; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
e , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
16.1.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f (z) |
2 z cos z |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
z0 |
2i |
|
|
|
|
|
|
|
|
|
|
|||||||||||
z |
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
16.1.13. |
|
|
|
|
|
|
, |
|
; |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6
16.1.14. |
f (z) |
|
|
|
3ez |
i 3e z |
z3 |
, |
|
z0 |
|
|
|
|
i |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
f (z) |
|
ze z |
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
16.1.15. |
|
|
z |
, |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
f (z) |
|
1 |
|
|
e |
2 z |
|
1 |
|
|
|
|
|
|
|
|
z |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
16.1.16. |
|
z |
|
|
|
|
|
|
|
z , |
|
|
|
|
0 |
2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
f (z) |
|
z 2 cos z |
|
|
1 |
e z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
16.1.17. |
|
2 |
, |
|
|
z0 |
|
i |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
16.1.18. |
f (z) |
2z sin z |
|
|
|
e z4 |
|
|
|
z0 |
|
|
i |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
16.1.19. |
f (z) z2 ez |
z2 |
, |
|
|
|
|
z0 |
|
|
i |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
f (z) |
|
2 sin z |
|
e z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
16.1.20. |
|
|
|
|
|
|
|
|
z |
|
, |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
16.1.21–16.1.30. Выясните, |
в |
каких |
точках |
z |
x |
i y |
комплексной плоскости |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
дифференцируема указанная функция. Чему равна производная в каждой из этих точек? |
|||||||||||||||||||||||||||||||||||||||||||||||
16.1.21. f (z) |
2zz |
|
|
|
2z ; |
|
|
|
|
|
|
|
|
16.1.22. |
|
f (z) |
4 |
|
|
2z |
2z zz ; |
||||||||||||||||||||||||||
16.1.23. f (z) |
|
zz z z ; |
|
|
|
16.1.24. f (z) |
9 |
|
|
3z |
zz ; |
||||||||||||||||||||||||||||||||||||
16.1.25. |
f (z) zz 5z 5z ; |
|
|
|
16.1.26. f (z) |
zz |
|
|
|
z |
4z ; |
||||||||||||||||||||||||||||||||||||
16.1.27. f (z) |
7z |
|
|
|
|
4z |
|
|
|
zz ; |
|
|
|
16.1.28. |
|
f (z) |
|
9z zz z ; |
|||||||||||||||||||||||||||||
16.1.29. |
f (z) |
|
3zz 3z z ; |
|
|
|
16.1.30. |
|
f (z) 6z 2z zz . |
||||||||||||||||||||||||||||||||||||||
16.2.1–16.2.10. Разложить функцию f(z) в ряд Лорана в окрестности точки z0 и |
|||||||||||||||||||||||||||||||||||||||||||||||
определить область сходимости этого ряда. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
16.2.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16.2.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
16.2.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16.2.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
16.2.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16.2.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
16.2.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16.2.8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
16.2.9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16.2.10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7
КОНТРОЛЬНАЯ РАБОТА № 6 Теория вероятностей.
17.1.11-17.1.20
17.1.11.В магазине было 10 покемонов и 15 деджимонов. Покемоны ломаются с вероятностью 0,1, а деджимоны – с вероятностью 0,3. Купленная игрушка сломалась. Какова вероятность, что это деджимон.
17.1.12.Прибор состоит из 6 узлов. Вероятность безотказной работы каждого узла в смену равна 0,9. Найти вероятность того, что за смену откажет ровно 2 узла.
17.1.13.В первом ящике 6 шаров: 1 белый, 2 красных, 3 синих. Во втором ящике 12 шаров: 2 белых, 6 красных, 4 синих. Из каждого ящика вынули по шару. Какова вероятность, что среди вынутых шаров нет синих?
17.1.14.В корзине 20 грибов: 15 лисичек, остальные белые. Вероятность того, что лисичка червивая – 0,01, для белого – 0,3. Какова вероятность того, что взятый гриб червивый.
17.1.15.В магазин вошло 7 покупателей. Вероятность совершить покупку для каждого равна 0,4. Найти вероятность того, что покупку совершат трое.
17.1.16.В урне 7 черных шаров и 3 белых. Наугад вынимают один за другим 2 шара. Найти вероятность того, что оба шара белые.
17.1.17.В букете 15 цветов: 5 гвоздик и 10 хризантем. Гвоздики ломаются с вероятностью 0,2, а хризантемы с вероятностью 0,1. Взятый цветок сломан. Какова вероятность, что это гвоздика.
17.1.18.Рабочий обслуживает 5 станков, каждый из которых может выйти из строя в течении смены с вероятностью 0,1. Найти вероятность того, что из строя выйдет только один станок.
17.1.19.В урне 7 черных шаров и 3 белых. Наугад вынимают один шар и возвращают в урну. Шары перемешивают, затем наугад вынимают второй шар. Найти вероятность того, что оба шара белые.
17.1.20.В коробке 40 пельменей: из них 30 больших, остальные маленькие. Большие разваливаются при варке с вероятностью 0,2, а маленькие с вероятностью 0,4. Какова вероятность, что взятая пельмешка развалилась.
17.2.11-17.2.20
17.2.11.Х – число выпадения герба при двух бросаниях монеты. Найти математическое ожидание случайной величины Х.
17.2.12.В партии 20% нестандартных деталей. Х – число нестандартных деталей среди 2 отобранных. Найти дисперсию случайной величины Х.
8
17.2.13.Вероятность попадания стрелком в мишень равна 0,7. Х – число попаданий при двух выстрелах. Найти математическое ожидание случайной величины Х.
17.2.14.Х – число выпадений четверки при двух бросаниях игральной кости. Найти математическое ожидание случайной величины Х.
17.2.15.Вероятность того, что прибор исправен равна 0,8. Х – число исправных приборов из двух выбранных. Найти математическое ожидание случайной величины Х.
17.2.16.На пути автомашины 2 светофора. Каждый из них с вероятностью 0,5 разрешает дальнейшее движение. Х – число светофоров, пройденных до первой остановки. Найти дисперсию случайной величины Х.
17.2.17.Станок-автомат производит 90% изделий первого сорта, 7% второго, а остальные третьего. X – число изделий первого сорта среди двух выбранных. Найти математическое ожидание случайной величины Х.
17.2.18.В коробке 20 конфет, из которых 4 с вареньем. X – число конфет с вареньем среди двух случайно выбранных. Найти дисперсию случайной величины Х.
17.2.19.Вероятность того, что в пакетике с чипсами попадется призовой купон равна 0,1. X – число пакетиков с купонами среди двух выбранных. Найти дисперсию случайной величины
Х.
17.2.20.5% лотерейных билетов – выигрышные. X – число выигрышных билетов среди двух выбранных. Найти математическое ожидание случайной величины Х.
17.2.31–17.2.40. Дискретная случайная величина X может принимать только два значения: х1 и х2 причем х1 < х2. Известны вероятность р1 возможного значения х математическое ожидание М(Х) и дисперсия D(X). Найти закон распределения этой случайной величины.
17.2.31. р1= 0,1; М(Х)=3,9; D(X)=0,09. 17.2.32. р1= 0,3; М(Х)=3,7; D(X)=0,21. 17.2.33. р1=0,5; М(Х)=3,5; D(X)=0,25. 17.2.34. р1=0,7; М(Х)=3,3; D(X)=0,21. 17.2.35. р1=0,9; М(Х)=3,1; D(X)=0,09. 17.2.36. р1=0,9; М(Х)=2,2; D(X)=0,36. 17.2.37. р1=0,8; М(Х)=3,2; D(X)=0,16. 17.2.38. р1=0,6; М(Х)=3,4; D(X)=0,24. 17.2.39. р1=0,4; М(Х)=3,6; D(X)=0,24. 17.2.40. р1=0,2; М(Х)=3,8; D(X)=0,16.
17.2.41–17.2.50. Случайная величина X задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины. Схематично построить графики функций F(x) и f(x).
9
|
0, |
x |
0; |
|
|
|
F (x) |
x2 , 0 |
x |
1; |
|
|
|
17.2.41. |
1, |
x |
1. |
|
|
|
|
|
|
|
|
|
|
|
0, |
х |
1; |
|
|
|
F (x) |
(x2 |
x)/2, 1 |
x |
2; |
||
17.2.42. |
1, |
x |
2. |
|
|
|
|
|
|
|
|
|
|
|
0, |
x |
0; |
|
|
|
F (x) |
x3 , 0 |
x |
1; |
|
|
|
17.2.43. |
1, |
x |
1. |
|
|
|
|
|
|
|
|
|
|
|
0, |
x |
0; |
|
|
|
F (x) |
3x2 |
2x, 0 x 1/ 3; |
||||
17.2.44. |
1, |
x |
1/ 3. |
|
|
|
|
|
|
|
|
|
|
|
0, |
x |
2; |
|
|
|
F (x) |
x / 2 1, 2 x 4; |
|
||||
17.2.45. |
1, |
x |
4. |
|
|
|
|
|
|
|
|
|
|
|
0, |
x |
0; |
|
|
|
F (x) |
x2 / 9, 0 x 3; |
|
||||
17.2.46. |
1, |
x |
3. |
|
|
|
|
|
|
|
|
|
|
|
0, |
x |
0; |
|
|
|
F (x) |
x2 / 4, 0 x 2; |
|
||||
17.2.47. |
1, |
x |
2. |
|
|
|
|
|
|
|
|
|
|
|
0, |
x |
|
/ 2; |
|
|
F (x) |
cos x, |
|
/ 2 |
x |
0; |
|
17.2.48.1, x 0.
|
0, x 0; |
|
F (x) |
2sin x, 0 x |
/ 6; |
17.2.49.1, x 
/ 6. 0, x 3
/ 4;
F (x) cos 2x,3 / 4 x |
; |
17.2.50.1, x 
.
17.3.11–17.3.20. Нормально распределенная случайная величина Х задана своими параметрами а (математическое ожидание) и 
(среднее квадратическое отклонение). Требуется:
а) написать плотность вероятности и схематически изобразить ее график; б) найти вероятность того, что Х примет значение из интервала ( ; );
10