2 курс ИНФОРМ ТЕХНОЛОГИИ ЖД ТРАНСП / 2 курс / Математическая логика_пособие
.pdfРОССИЙСКАЯ ОТКРЫТАЯ АКАДЕМИЯ ТРАНСПОРТА
________________________________________________________________
Одобрено кафедрой «Высшая и прикладная математика»
МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ
Методические указания по решению задач на практических занятиях
для студентов–заочников II курса специальности 230400.62 Информационные системы и технологии
Москва – 2012
Задание №1.
Задана логическая формула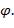 
От нее перейти к эквивалентной ей формуле 
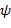так, чтобы последняя не содержала знаков операции 
и 
. Исходя из таблиц истинности булевых операций доказать, что формулы 
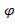и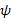 
логически эквивалентны. Для формулы 
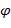найти СКНФ
и СДНФ.
Приведем некоторые логические законы исчисления высказываний, которые понадобятся нам:
1) Правила замены операции импликации
(1)
(2)
2) Правила замены операции эквивалентности
(3)
(4)
ПРИМЕР. Пусть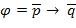 
. Используя (1), получаем 
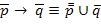. Поскольку 
,
то окончательно имеем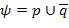 
. Теперь докажем эквивалентность формул 
и 
, и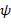спользуя таблицы истинности операций отрицания, дизъюнкции, конъюнкции и импликации.
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
0 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
1 |
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
1 |
1 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
Для формулы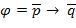 
построим СДНФ. Поскольку значение 
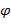равно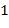 
на наборах переменных 
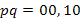, и 
, то каждому из них соответствует следующие произведения этих
переменных:
, 
, 
.
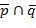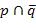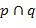Для получения СДНФ построим дизъюнкцию этих произведений:
.
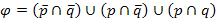Для получения CКНФ выпишем термы, на которых функция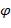 
принимает значения,
равные 0 (или, что все равно, значения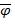 
равны 
). В нашем случае это терм (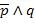
) т.е.,
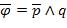. Далее в каждом таком терме инвертируем переменные и образуем из них
дизъюнкцию. Затем все эти дизъюнкции объединяем через знаки конъюнкции. В нашем случае терм 
заменяем на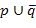 
. Поскольку терм только один, то это и есть СКНФ для функции
Задание №2.
Найти область истинности предиката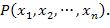 
Напомним, что областью истинности этого предиката называются те упорядоченные наборы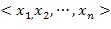 
, на которых предикат имеет значение, равное 
.
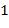ПРИМЕР. Задан предикат |
, где ( |
и |
.
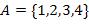Множество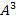 
есть множество всех упорядоченных троек (
, где 
.
Для решения рассматриваемой задачи необходимо построить все возможные
упомянутые тройки (общее |
их число равно |
) и |
для каждой из них проверить |
|
справедливость неравенства |
. Например, для тройки |
оно не выполняется, |
||
т.к. неравенство |
неверно. Следовательно, |
эта |
тройка |
не принадлежит области |
истинности предиката. Рассмотрим другую тройку –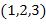 
. Для нее 
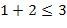, т.е. неравенство
справедливо и эта тройка принадлежит области истинности предиката. Осуществив перебор всех троек и проверив для каждой из них справедливость неравенства, получаем следующую область истинности предиката:
.
Задание №3.
Задана функция от нечетких переменных. Требуется упростить эту функцию.
Отметим, что для упрощения обычных логических функций используются все известные логические законы, включая закон тождества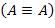 
, непротиворечивости 
,
исключенного |
третьего |
, |
свойства |
констант |
|
, |
идемпотентности |
, |
|
ассоциативности |
|
|
, |
закон поглощения |
|
, закон де Моргана |
|
и т.д. |
|
Заметим, что для упрощения функций от нечетких переменных используются те же логические законы, но два из них (непротиворечивости и исключенного третьего) не имеют места.
ПРИМЕР. Задана функция |
. Выполняем последовательно ее |
преобразования: |
|
Задание № 4.
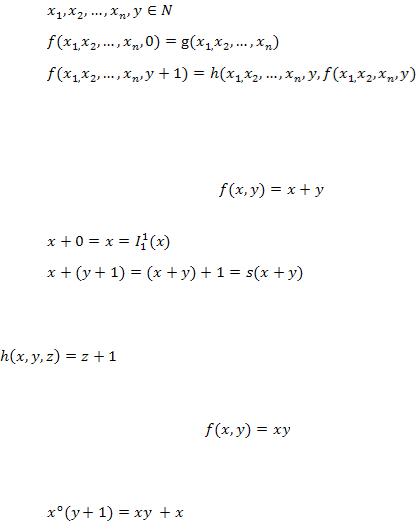
Вначале напомним следующее определение. Пусть задана некоторые числовые функции: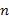 
-арная функция 
и 
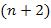-арная функция 
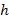. Говорят, что 
-арная функция 
возникает
из функций 
и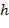 
примитивной рекурсией, если для всех имеем
,
Теперь перейдем к постановке задачи. Пользуясь определением примитивно рекурсивной функции, показать, что числовая функция примитивно рекурсивна.
ПРИМЕР 1. Пусть |
. Это двуместная функция удовлетворяет |
соотношениям |
|
, |
|
|
. |
Следовательно, рассматриваемая функция возникает из примитивной рекурсивных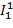 
,
операцией примитивной рекурсии и потому заданная функция примитивно
рекурсивна.
ПРИМЕР 2. Пусть |
. Это двуместная функция удовлетворяет схеме |
примитивной рекурсии
,
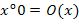с начальными примитивно рекурсивными функциями
, 
.
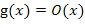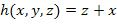Поэтому рассматриваемая функция примитивно рекурсивна.
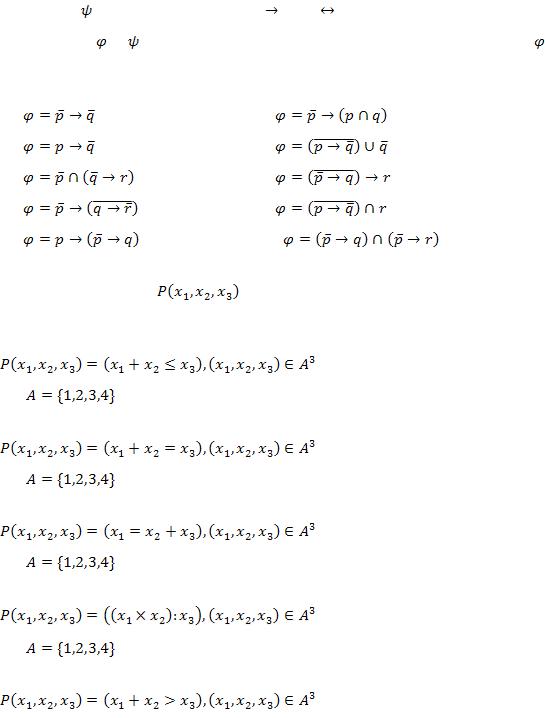
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РЕШЕНИЯ НА ПРАКТИЧЕСКИХ ЗАНЯТИЯХ
Работу необходимо выполнять аккуратно, любыми чернилами, кроме красных. При выполнении контрольной работы обязательно должны быть подробные вычисления и четкие пояснения к решению задачи. В каждой задаче должен быть ответ. В конце работы студент должен поставить дату и свою подпись. Если перечисленные требования не выполнены, то преподаватель имеет право вернуть работу, не проверяя еѐ.
Номера вариантов задач контрольной работы, который должен решить студент, определяются последней цифрой учебного шифра студента. Так, если студент имеет шифр 1010-АТС-1425, то он должен решить задачи с номерами 5, 15, 25, 35.
Задачи 1- 10.Задана формула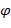 
. От формулы 
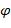перейти к эквивалентной ей формуле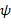 
так, чтобы формула |
не содержала связок « » и « ». Исходя из истинностных таблиц |
|
доказать, что формулы |
и равносильны (логически эквивалентны). Для формулы найти |
|
СКНФ и СДНФ. |
|
|
1. |
|
6. |
2. |
|
7. |
3. |
|
8. |
4. |
|
9. |
5. |
|
10. |
Задачи 1120. Предикат |
задан своей называющей формой. Найти область |
|
истинности предиката. |
|
|
11. |
|
, |
где |
. |
|
12. |
|
, |
где |
. |
|
13. |
|
, |
где |
. |
|
14. |
|
, |
где |
. |
|
15. |
|
, |
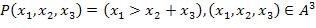
где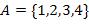 
.
16. 
,
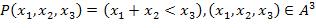где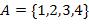 
.
17. 
,
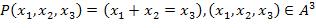где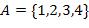 
.
18. 
,
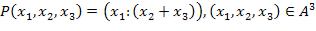где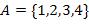 
.
19.
где 
.
20. 
,
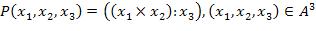где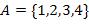 
.
Задачи 2130. Задана функция 
от нечетких переменных. Упростить эту нечеткую функцию.
21. 
,
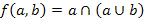22. 
,
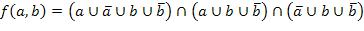23. 
,
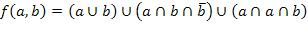24. 
,
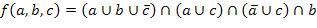25. 
,
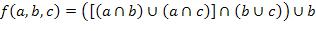26. 
,
27. 
,
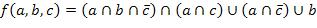28. 
,
29. 
,
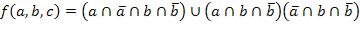30. 
.
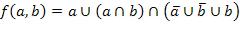Задачи 3140. Пользуясь определением примитивно рекурсивной функции, показать, что числовая функция 
примитивно рекурсивной.
31. |
, |
32. |
, |
33. |
, |
34. |
, |
35. |
, |
36. |
, |
37. |
, |
38. |
, |
39. |
, |
40. |
. |