II.Энергия механического движения.
Изменение энергии системы пропорционально работе А, совершённой внешними силами, приложенными к системе:
E = E2 – E1 = A
К механической энергии относят два вида энергии – кинетическую (ЕК) и потенциальную (ЕП). Чтобы получить выражение энергии в виде функции параметров состояния механического движения, надо найти, как изменяется величина энергии с изменением величины параметров.
Кинетической энергией называется энергия движущегося тела.
Для вычисления кинетической энергии подсчитаем работу, которую должна произвести результирующая сила F, чтобы тело массыmизменило скорость своего движения отV1доV2.
Умножим обе части равенства на Vdt=dS
(4)
– кинетическая энергия тела.
Или по другому: dA=Fdr
|
А = ЕК |
Работа равна изменению кинетической энергии тела, чтобы изменить скорость его движения от V1доV2. |
Если действует ещё сила трения, то Aтр< 0 и кинетическая энергия тела будет уменьшаться.
|
Потенциальная энергия |
Энергия, обусловленная взаимным расположением тел или частей одного и того же тела и характером их взаимодействия. |
Потенциальная энергия системы тел (или тела) может быть определена, если указаны взаимное расположение тел в системе и силы, действующие между ними.
|
|
В процессе перемещения
материальной точки на
|
внешняя сила
совершит работу
.
При этом перемещении скорость тела
не изменилась (былаV=
0 и сталаV= 0), значит в
результате совершённой работы,
произошло изменение другой (не
кинетической) формы энергии, зависящей
от координат положения тела, т.е. нужно
говорить о потенциальной энергии.Обозначим через dEП– изменение потенциальной энергии при перемещении точки в силовом поле. Согласно определению работы, можно записать:
(5)
|
Работа, совершаемая силами F, действующими на материальную точку при её перемещении, равна изменению её потенциальной энергии. |
Равенство (5) надо понимать алгебраически:
а) если dA> 0, то потенциальная энергия уменьшается (dEП< 0).
б) если dA< 0, то потенциальная энергия возрастает (dEП > 0).
Учитывая, что
,
имеем:
(6)
Это соотношение между силой и потенциальной энергией является одним из основных соотношений механики, или
(7)
Выражение
называетсяградиент изменения
потенциальной энергиина путиS.
Из этого выражения (7) следует:
а) если
–
энергия возрастает, тоFбудет отрицательна.
Сила направлена всегда в сторону уменьшения потенциальной энергии.
б) производная обращается в ноль в точках, где функция достигает максимума или минимума, а это значит – где потенциальная энергия имеет максимум или минимум, там сила равна нулю.
Изменения потенциальной энергии ЕПзависят от относительного изменения взаимного расположения взаимодействующих тел. Следовательно,потенциальная энергияU, относится не только к выбранной материальной точке, но и ко всей системе и представляет собойэнергию взаимодействия тел(поднятый над Землёй камень и Земля – потенциальная энергия взаимодействия камня и Земли).
Уравнение (5) не даёт полного определения величины потенциальной энергии в каждой точке, а определяет лишь изменение потенциальной энергии при переходе от точки к точке. Абсолютная величина ЕПзависит от выбора начала отсчёта потенциальной энергии (где потенциальная энергия равна нулю). Обычно, за начало отсчёта выбирают такое положение, при котором взаимодействие практически отсутствует (когда тела удалены в бесконечность).
Вычислим величину потенциальной энергии в двух случаях:
1. Потенциальная энергия тяготения.
dEп = -Fdr
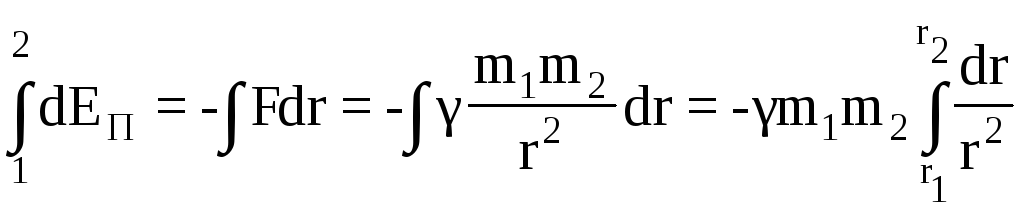
В частном случае, при r1= 0, (на поверхности Земли),r2=H, (над поверхностью Земли)
E=mgH
2. Потенциальная энергия упругодеформированного тела.
dA = Fdx = kxdx
