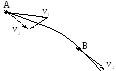Лекция №1. Механика поступательного прямолинейного и криволинейного движений.

I. Введение.

1. Наиболее простым примером механического движения является движение материальной точки.

Материальной точкой называется абстракция реального тела, размерами и формой которого можно пренебречь по сравнению с размерами других тел или расстояниями до них, обладающего массой равной массе тела.

2. Для определения положения телав пространстве нужно использовать систему отсчета. Существует (наиболее употребительные) два способа описания движения тела (точки): векторный способ и координатный.

Рассмотрим движение материальной точки в прямоугольной декартовой системе координат, поместив начало координаты в некую неподвижную точку О.

	Положение точки А определяется заданием трех координат X, Y иZ. А ее координаты изменяются с течением времени. По этому в общем случае движение будет определено, заданием трех уравнений.
		X = X(t) Y = Y(t) Z = Z(t)	Кинематические уравнения движения точки	(1)
	Исключив из уравнения время, получим уравнение линии, движения описываемой движущейся точкой в пространстве и называется траекторией движения. Длина участка траектории, пройденной точкой за времяt, называетсядлиной пути(путь)S.S– величина скалярная.

Уравнение пути: S=f(t)S≥0;

В зависимости от формы траектории движения:

а) прямолинейное ^_______

б) криволинейное ~~~~, O(частный случай – вращательное движение)

Вместо трех уравнений для координат движущейся точки ее движение можно задать одним векторным уравнением:

, (2)

где – радиус-вектор проведенный из начала координат в точку 1.

Вектор , проведенный из начала в конец положения движущийся точки, называетсявектором перемещения.

3. Кинематически характеризировать движениеточки формой траектории, путёмSи радиус-вектором– недостаточно, надо указать быстроту перемещения.

Пусть материальная точка движется по криволинейной траектории. Вектор перемещения представляет приращение радиуса-вектораза время Δt: Величину характеризующую быстроту изменения положения точки, определяют отношением: , где – средняя скорость движения.

Вектор совпадает по направлению с. Если в выраженииперейти к пределу при∆t→ 0, то получим выражениемгновенной скорости, т.е. скорость в данный момент времени:

(3)

Это значит, что в данный момент времени равен производнойи направлен по касательной к траектории в данной точке (как и) в сторону движения точки.

Из математики известно, что модуль малого приращения равен длинеdsсоответствующей ему дуги траектории, т.е.

Из последнего следует:

Для нахождения пути, пройденного телом за промежуток времени Δt, надо найти интеграл:

4. Скорость механического движенияв большинстве случаев не остается постоянной, а меняется со временем либо по величине, либо по направлению, либо по величине и направлению одновременно.

Тело двигалось из точки А в точку В. Перенеся вектор в точку А находим приращение скорости: – среднее ускорение Используя предыдущие рассуждения, получим: – мгновенное ускорение.

Ускорение– физическая величина характеризующая быстроту изменения скорости.

Ускорение – вектор, равный производной от вектора скорости по времени и совпадающий по направлению с вектором изменения скорости dvза малый интервал времениdt.

Легко показать, что:

Зная кинематические уравнения движения можно по аналогии получить:

а для модулей векторов скорости и ускорения получим:

Пример: найти уравнения [v=v(t) иS=S(t)] прямолинейного движения.

Используем уравнение ; пусть а =const, тогда ∆v=a∙∆t;v=v₀+at

Далее:

dS = (v₀ + at)dt;