
твір
.docx
 =
=
Очевидно,
що
 =
= тоді і лише тоді, коли
тоді і лише тоді, коли
 )
= 0.
Тобто перевірка збіжності послідовності
(
)
= 0.
Тобто перевірка збіжності послідовності
( )
точок простору
)
точок простору
 )
до точки
)
до точки
 зводиться до перевірки того факту, що
числова послідовність
зводиться до перевірки того факту, що
числова послідовність
 ))
є нескінченно малою.
))
є нескінченно малою.
Теорема
1. Якщо
послідовність точок простору
 )
має границю, то вона єдина.
)
має границю, то вона єдина.
Доведення.
Нехай
у просторі
 )
існує послідовність (
)
існує послідовність ( ),
для якої
),
для якої
 =
= і
і
 =
= ,
причому
,
причому

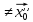 .
.
Оскільки
 =
= ,
то для будь
,
то для будь
 якого
якого
 ,
зокрема для
,
зокрема для

 ,
існує номер
,
існує номер
 такий, що всіх
такий, що всіх виконується нерівність
виконується нерівність


 .
.
А
оскільки
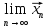 =
= ,
то для
,
то для

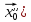 ,
існує номер
,
існує номер
 такий, що всіх
такий, що всіх виконується нерівність
виконується нерівність

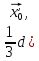
 .
.
Нехай
 .
Тоді для всіх
.
Тоді для всіх
 виконуються то обидві нерівності. А
тому, взявши конкретне
виконуються то обидві нерівності. А
тому, взявши конкретне
 .
Маємо:
.
Маємо:



 .
.
Одержане
протиріччя спростовує припущення, тобто
не існує у просторі
 )
збіжної послідовності, яка б мала більше
однієї границі.
)
збіжної послідовності, яка б мала більше
однієї границі.
Нехай
маємо не порожню множину F
точок простору
 ),
і нехай
),
і нехай
 послідовність точок цієї множини. Якщо
ця послідовність збігається, то належність
границі кожної такої послідовності
множині F
є характеристичною властивістю так
званих замкнених множин.
послідовність точок цієї множини. Якщо
ця послідовність збігається, то належність
границі кожної такої послідовності
множині F
є характеристичною властивістю так
званих замкнених множин.
Означення.
Множина
F
точок простору
 )
називається замкненою, якщо для будь
)
називається замкненою, якщо для будь
 якої збіжної послідовності
якої збіжної послідовності
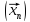 точок множини F
точок множини F
 .
.
Для
прикладу, будь
 яка скінченна множина точок простору
яка скінченна множина точок простору
 )
є замкненою множиною, будь
)
є замкненою множиною, будь
 яка область в об’єднанні із своєю межею
є замкненою.
яка область в об’єднанні із своєю межею
є замкненою.
Нехай
маємо послідовність ( )
= ((
)
= (( ))
простору
))
простору
 .
Очевидно, що вона породжує дві числові
послідовності
.
Очевидно, що вона породжує дві числові
послідовності
 ,
,
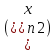 ,
які природ називати координатними
послідовностями. Аналогічно, якщо (
,
які природ називати координатними
послідовностями. Аналогічно, якщо ( )
= ((
)
= (( ))
послідовність точок простору
))
послідовність точок простору
 ,
то вона породжує три координатні
послідовності
,
то вона породжує три координатні
послідовності
 Зв’язок між збіжністю послідовності
(
Зв’язок між збіжністю послідовності
( )
і координатних послідовностей
розкривається в наступній теоремі.
)
і координатних послідовностей
розкривається в наступній теоремі.
Теорема
. Послідовність ( )
= ((
)
= (( ))
точок простору
))
точок простору
 ((
(( )
= ((
)
= (( ))
послідовність точок простору
))
послідовність точок простору
 збігається тоді і тільки тоді, коли
збігаються координатні послідовності
збігається тоді і тільки тоді, коли
збігаються координатні послідовності
 ,
,
 (
( ,
причому
,
причому
 (
(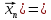
 ,
,
 (
(
 ,
,

Доведення.
Проведемо
для послідовності точок простору
 .
.
Необхідність.
Нехай
послідовність ((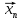 )
= ((
)
= (( ))
збігається причому
))
збігається причому
 (
(
 = (
= ( ).
).
Доведемо,
що
 =
=
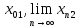 =
=
 =
=

Якщо
 (
(
 ,
то для
,
то для
 існує
номер
існує
номер
 такий, що всіх
такий, що всіх
 виконується нерівність
виконується нерівність
 .
.
А оскільки
 ׀
׀

для
і
=
1,2,3, то


 ׀
׀
 .
А це й означає, що
.
А це й означає, що
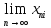 =
=

для і = 1,2,3.
Достатність.
Нехай
послідовність (( )
= ((
)
= (( ))
координатні послідовності
))
координатні послідовності
 збігаються,
причому
збігаються,
причому
 =
=
 = =
= = =
=
 Тоді для
Тоді для
 ,
зокрема для
,
зокрема для
 , існує номер
, існує номер
 такий, що всіх
такий, що всіх
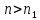 виконується нерівність
виконується нерівність
 ׀
׀
 .
Для
.
Для
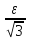 існує номер
існує номер
 такий, що всіх
такий, що всіх
 виконується нерівність
виконується нерівність
 ׀
׀
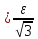 .
І, нарешті, для
.
І, нарешті, для
 існує номер
існує номер
 такий, що всіх
такий, що всіх
 виконується нерівність
виконується нерівність
 ׀
׀
 .
Нехай
.
Нехай
 .
Тоді для
.
Тоді для
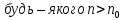 виконується нерівність
виконується нерівність
 ׀
׀
 і
для кожного і
=
1,2,3.
і
для кожного і
=
1,2,3.
Отже,
для всіх

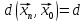 ((
(( ),
(
),
( ))
=
))
=
=
 =
=
 .
.
А
це й означає, що
 (
(
 = (
= ( ).
).
В
аналізі числових функцій ряд властивостей
неперервних функцій істотно залежить
від структури області, на якій вони
визначені. Маємо на увазі властивості
неперервних функцій, визначених на
відрізку. Звичайно ми можемо означити
відрізок і в
 .
Однак для функцій двох і трьох змінних
відрізок аж ніяк не є найбільш популярною
областю визначення. Бажано виділити
достатньо широкий клас множин, на яких
неперервні функції мають ті ж властивості,
що й на числових відрізків.
.
Однак для функцій двох і трьох змінних
відрізок аж ніяк не є найбільш популярною
областю визначення. Бажано виділити
достатньо широкий клас множин, на яких
неперервні функції мають ті ж властивості,
що й на числових відрізків.
У
зв’язку з цим звернемо увагу на одну
теорему, яка досить часто використовувалась
в аналізі числових функцій, а саме на
теорему Больцано
 Вейєрштрасса,
у якій стверджується, що з кожної
обмеженої числової послідовності можна
виділити збіжну підпослідовність.
Вейєрштрасса,
у якій стверджується, що з кожної
обмеженої числової послідовності можна
виділити збіжну підпослідовність.
Якраз властивість, яка полягає у тому, що з кожної послідовності точок множини можна виділити підпослідовність, збіжну до точки цієї множини, і є характеристичною властивістю множин, роль яких в аналізі функцій двох і трьох змінних схожа з роллю відрізків в аналізі числових функцій однієї змінної.
Теорема.
(Больцано
 Вейєрштрасса).
З
кожної обмеженої послідовності
(
Вейєрштрасса).
З
кожної обмеженої послідовності
( простору
простору
 )
можна виділити збіжну підпослідовність.
)
можна виділити збіжну підпослідовність.
Доведення.
Нехай
послідовність ( )
= ((
)
= (( ))
точок простору
))
точок простору
 обмежена. Це означає, що існує прямокутник
обмежена. Це означає, що існує прямокутник

такий,
що для всіх
 (
( )
)

 ,
причому для всіх
,
причому для всіх

 [
[ ],
],
 [
[ ].
Згідно теореми Больцано
].
Згідно теореми Больцано
 Вейєрштрасса
для числових послідовностей
Вейєрштрасса
для числових послідовностей
 ),
границя якої нехай рівняється
),
границя якої нехай рівняється
 .
За підпослідовністю
.
За підпослідовністю
 )
побудуємо піпослідовність
)
побудуємо піпослідовність
 )
послідовності
)
послідовності
 ),
яка звичайно обмежена. А тому з неї можна
виділити збіжну підпослідовність
),
яка звичайно обмежена. А тому з неї можна
виділити збіжну підпослідовність
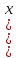 ),
границя якої нехай
),
границя якої нехай
 ).
Тоді послідовність
).
Тоді послідовність
 )
як підпослідовність збіжної послідовності
має границю
)
як підпослідовність збіжної послідовності
має границю
 ).
Отож маємо підпослідовність
).
Отож маємо підпослідовність
 ,
,
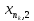 )
таку, що
)
таку, що


 ,
,
 .
.
В
силу теореми підпослідовність
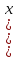 ,
,
 )
послідовності (
)
послідовності ( )
збігається.
)
збігається.
Означення.
Множина
К точок простору
 )
називається компактною множиною, якщо
з кожної послідовності точок множини
К можна виділити підпослідовність, яка
збігається до точки цієї множини.
)
називається компактною множиною, якщо
з кожної послідовності точок множини
К можна виділити підпослідовність, яка
збігається до точки цієї множини.
Теорема.
Множина
К точок простору
 )
є компактною тоді і лише тоді, коли вона
обмежена і замкнена.
)
є компактною тоді і лише тоді, коли вона
обмежена і замкнена.
В
аналізі числових функцій однієї змінної
важливу роль відіграє властивість
фундаментальності послідовності,
оскільки є необхідною і достатньою
умовою збіжності. А оскільки при означенні
фундаментальності ,,
послідовність ( )
фундаментальна :=
)
фундаментальна :=
 ҆ ҆ фігурує
тільки відстань, то його множин перенести
в довільний метричний простір, зокрема
в
҆ ҆ фігурує
тільки відстань, то його множин перенести
в довільний метричний простір, зокрема
в
 )
.
)
.
Означення.
Послідовність
( )
точок простору
)
точок простору
 )
називається фундаментальною (послідовністю
Коші), якщо для будь
)
називається фундаментальною (послідовністю
Коші), якщо для будь
 якого
якого
 існує номер
існує номер
 такий, що всіх
такий, що всіх
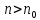 і для будь
і для будь
 якого натурального
якого натурального виконується
нерівність
виконується
нерівність
 .
.
Теорема
5. Послідовність
( )
= ((
)
= ((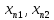 ))
точок простору
))
точок простору
 (
( )
= ((
)
= (( ))
простору
))
простору
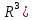 є фундаментальною тоді і лише тоді, коли
фундаментальні координатні послідовності
є фундаментальною тоді і лише тоді, коли
фундаментальні координатні послідовності
 ,
,
 (
( .
.
Доведення.
Необхідність.
Нехай
послідовність ( )
= ((
)
= (( ))
фундаментальна. Тоді в силу означення
для будь
))
фундаментальна. Тоді в силу означення
для будь
 якого
якого
 існує номер
існує номер
 такий, що всіх
такий, що всіх
 і для будь
і для будь
 якого натурального
якого натурального виконується
нерівність
виконується
нерівність

А
оскільки для будь
 яких
яких
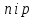
׀ ׀
׀ і
׀
і
׀ ׀
׀ ,
,
то
маємо, що для будь
 якого
якого
 маємо номер
маємо номер
 такий, що для всіх
такий, що для всіх
 і для будь
і для будь
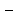 якого натурального
якого натурального виконується
нерівність ׀
виконується
нерівність ׀ ׀
׀ ,
а це означає, що послідовність (
,
а це означає, що послідовність ( того
ж
того
ж
 виконується нерівність ׀
виконується нерівність ׀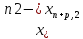 ׀
׀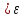 для
всіх
для
всіх
 і для будь
і для будь
 якого натурального
якого натурального ,
що свідчить про фундаментальність
послідовності
,
що свідчить про фундаментальність
послідовності
 .
.
Достатність.
Нехай
послідовність
 ,
,
 фундаментальні,
тобто для будь
фундаментальні,
тобто для будь
 якого
якого
 ,
зокрема для
,
зокрема для
 , існує номер
, існує номер
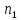 такий, що всіх
такий, що всіх
 і для будь
і для будь
 якого натурального
якого натурального виконується
нерівність ׀
виконується
нерівність ׀ ׀
׀ і
номер
і
номер
 такий, що для всіх
такий, що для всіх
 і будь
і будь
 якого натурального
якого натурального виконується
нерівність
׀
виконується
нерівність
׀ ׀
׀ .
Нехай
.
Нехай
 .
Тоді для будь
.
Тоді для будь
 якого
якого
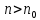 і для будь
і для будь
 якого натурального
якого натурального виконується
обидві нерівності. Отже, для всіх
виконується
обидві нерівності. Отже, для всіх
 і для будь
і для будь
 якого натурального
якого натурального
 =
=
 .
.
А
це й означає, що послідовність (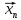 )
фундаментальна.
)
фундаментальна.
Теорема.
(критерій
Коші). Послідовність
точок простору
 )
збіжна тоді і тільки тоді, коли вона
фундаментальна.
)
збіжна тоді і тільки тоді, коли вона
фундаментальна.
Доведення.
Необхідність.
Нехай
послідовність ( )
збіжна і нехай
)
збіжна і нехай
 (
(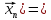
 бто
для будь
бто
для будь
 якого
якого
 ,
зокрема для
,
зокрема для
 ,
існує номер
,
існує номер
 такий, що всіх
такий, що всіх
 виконується нерівність
виконується нерівність
 будь
будь
 якого натурального
якого натурального
 ,
маємо, що і
,
маємо, що і
 .
А тому для всіх
.
А тому для всіх
 і для будь
і для будь
 якого натурального
якого натурального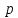 виконується нерівність
виконується нерівність


 .
.
Достатність.
Нехай
послідовність ( )
фундаментальна. Тоді згідно з теоремою
5 фундаментальними, а отже, збіжними,
будуть координатні послідовності.
Останнє гарантує збіжність послідовності
(
)
фундаментальна. Тоді згідно з теоремою
5 фундаментальними, а отже, збіжними,
будуть координатні послідовності.
Останнє гарантує збіжність послідовності
(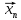 ).
).
Метричні
простори, у яких кожна фундаментальна
послідовність є збіжною називаються
повними.
Таким чином простори
 повні (без дірок).
повні (без дірок).
