
твір
.docxПлан твору
-
Двовимірні та тривимірні евклідові простори
-
Множини
 і
і
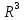 .
Наділення їх алгебраїчною структурою.
.
Наділення їх алгебраїчною структурою.
-
1.2 Наділення геометричною структурою.
1.3 Криві та області на площині. Криві, області та поверхні у просторі.
-
Топологічні властивості просторів
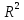 і
і
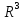
-
Послідовності точок просторів
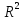 і
і
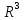 .
Збіжні послідовності.
.
Збіжні послідовності. -
Властивості границь послідовностей.
-
Теорема Больцано
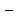 Вейєрштрасса.
Компактні властивості.
Вейєрштрасса.
Компактні властивості. -
Критерій Коші збіжності послідовності. Повнота просторів
 і
і
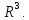
-
Двовимірні та тривимірні евклідові простори
При
побудові теорії числових функцій двох
і трьох змінних базовими множинами
будуть множина
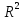 –
множина всіх можливих пар і
–
множина всіх можливих пар і
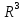 –
множина всіх можливих трійок дійсних
чисел, тобто
–
множина всіх можливих трійок дійсних
чисел, тобто

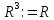
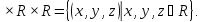
З
геометричної точки зору
 точка на площині,
точка на площині,
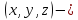 точка
у просторі.
точка
у просторі.
Означимо на цих множинах такі дві операції:

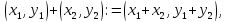
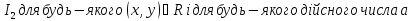
a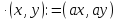 ;
;
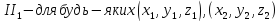
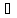
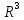
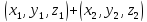
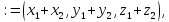
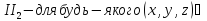
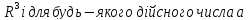
a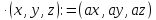 .
.
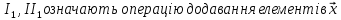 =
(
=
( ,
,
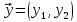 ,
,
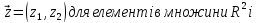
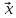 = (
= ( ,
,
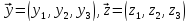 для
елементів множини
для
елементів множини
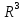 .
.
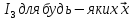 =
(
=
(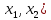 ,
,
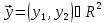
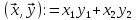 ;
;
 =
(
=
( ,
,
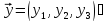
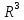
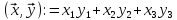 ;
;
яку
називають скалярним
(внутрішнім) добутком
елементів множин
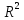 і
і
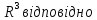 .
.
Знову таки в очевидний спосіб перевіряється, що так означені операції задовольняють властивості:
1°.
 ,
,
2°.
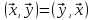 ,
,
3°.
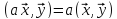 ,
,
4°.
 =
=
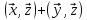
для
всіх
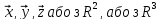 ,
для всіх
,
для всіх
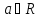 .
.
Властивості
1°
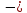 4°
є
характеристичними властивостями
евклідового простору (лінійного простору
із скалярним добутком), а тому лінійні
простори
4°
є
характеристичними властивостями
евклідового простору (лінійного простору
із скалярним добутком), а тому лінійні
простори
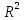 і
і
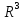 наділені операціями
наділені операціями
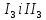 є евклідовими просторами.
є евклідовими просторами.
З
кожним елементом
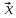 = (
= (
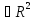 пов’яжемо
число
пов’яжемо
число
 :=
:=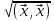 =
=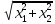
(читається
норма елемента
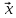 ),
а з кожним елементом
),
а з кожним елементом
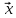 = (
= (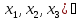
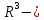 число
число
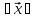 :=
:=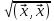 =
=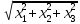
(Якщо
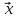 точка на координатній площині (у
координатному просторі), то
точка на координатній площині (у
координатному просторі), то
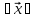 є довжина вектора
є довжина вектора
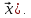 Очевидно, що як у першому так і другому
випадку
Очевидно, що як у першому так і другому
випадку
1°.
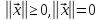
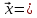
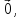
2°.
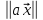 =׀
=׀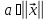 ,
,
3°.
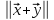

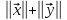 .
.
Для
прикладу, перевіримо виконуваність
нерівності 3° у просторі
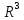 .
Якщо або
.
Якщо або
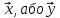 є нуль-елемент, то
є нуль-елемент, то
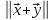

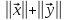 .
.
Нехай
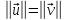 =1.
Тоді
=1.
Тоді
0
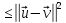 =
=
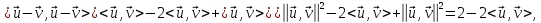
тобто
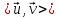
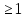 .
А тому для будь
.
А тому для будь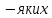 ненулевих
елементів з
ненулевих
елементів з
 :
:
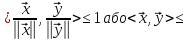
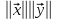 .
.
Таким
чином для будь
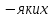
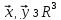 виконується нерівність
виконується нерівність
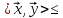
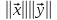 .
.
Скориставшись останньою нерівністю, маємо
 .
.
Звідси
дістаємо
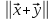
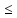
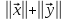 .
.
Властивості
1°
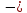 3°
є
характеристичними властивостями
нормованого простору (лінійного простору
нормою ), а тому лінійні простори
3°
є
характеристичними властивостями
нормованого простору (лінійного простору
нормою ), а тому лінійні простори
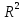 і
і
 наділені нормою, що породжується
скалярним добутком.
наділені нормою, що породжується
скалярним добутком.
Нерівність
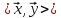
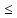
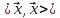
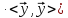 вказує на те, що існує кут
вказує на те, що існує кут
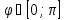 такий, що
такий, що
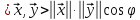 .
Якраз кут, що визначається з рівняння
.
Якраз кут, що визначається з рівняння
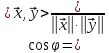
або
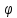 =
=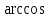
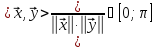
і
називається кутом
між векторами
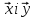 .
І цілком природно вважати, що вектори
.
І цілком природно вважати, що вектори
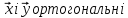 ,
якщо їх скалярний добуток рівняється
нулю.
,
якщо їх скалярний добуток рівняється
нулю.
І,
нарешті, норма дає можливість означити
відстань між елементами просторів
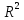 і
і
 ,
а саме
,
а саме
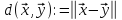 =
=

для
будь
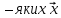 = (
= (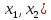 ,
,
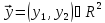
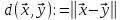 =
=
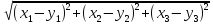
для
будь
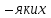
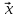 = (
= ( ,
,
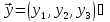
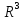 ,
,
тобто
на множинах
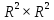 і
і
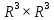 задається функція
задається функція
 ,
значення якої задовольняють такі
властивості:
,
значення якої задовольняють такі
властивості:
1°.
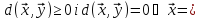
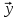 ,
,
2°.
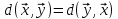 ,
,
3°.
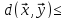
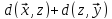
для
всіх
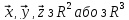 .
.
Останні
три властивості є характеристичними
властивостями метричного простору, а
тому
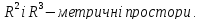
Підсумовуючи,
зазначимо, що якраз множини
 будуть базисними для розбудови теорії
числових функцій двох і трьох змінних,
причому в багатьох випадках визначальна
роль у цій розбудові за алгебраїчними
і геометричними властивостями цих
множин.
будуть базисними для розбудови теорії
числових функцій двох і трьох змінних,
причому в багатьох випадках визначальна
роль у цій розбудові за алгебраїчними
і геометричними властивостями цих
множин.
Означення 1. Евклідів простір називається гільбертовим або H-простором (від прізвища Hilbert), якщо він повний за нормою, яка породжується скалярним добутком цього
евклідового простору.
Часто в підручниках в означенні простору Гільберта додається ще умова нескінченновимірності простору.
Якщо скалярний добуток визначений над полем комплексних чисел, то простір називається комплексним H-простором. У випадку скалярного добутку над полем дійсних чисел простір називається дійсним гільбертовим простором.
Простір Гільберта є узагальненням простору зі скалярним добутком, тому його “геометрія” ближче, ніж в будь-якому банаховому просторі, до класичної евклідової геометрії. Це дало можливість розвинути функціональний аналіз на основі гільбертового простору значно повніше, ніж на основі загальних нормованих просторів. Теорія гільбертового простору виділилася в самостійний розділ функціонального аналізу зі своїми результатами та методами.
В даний час в математиці чітко проявляється тенденція переходу до проблем, зв’язаних з прикладними задачами. З іншого боку, значно ускладнилися моделі, які описують процеси в економіці та природознавстві. Виявилося, що найчастіше абстрактна теорія більш проста, перенесення її результатів на проблеми математичної економіки дає кращі результати, ніж розв'язування цих проблем “в лоб”.
Приклад Скінченновимірні евклідові та гільбертів простір:
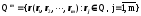 ,
,
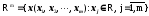 .
.
Покажемо, що Qm є евклідовим, але не гільбертовим простором, а Rm – m-вимірний гільбертів простір.
Скалярні добутки в цих просторах вводяться за формулами
 ,
,
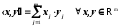 .
.
Виконання аксіом скалярного добутку в цих просторах розглянуто в прикладі 15.... Ці простори – евклідові. Скалярні добутки породжують норми :
 ,
,
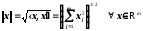 .
.
Простір Qm не є повним за нормою: існують фундаментальні послідовності Коші в Qm , границя яких не збігається до елемента в Qm , а є елементом в Rm.
Нагадаємо, що послідовності
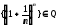 ,
,
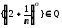
мають границі e та 2 відповідно. За критерієм Коші в R можемо одержати оцінку
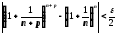 ,
,
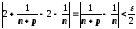 .
.
Тоді послідовність
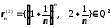
є фундаментальною в Q2 :
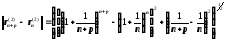 <
<
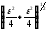 <
.
<
.
Проте

 .
.
Простір Q2 не повний, не гільбертів. Для доведення повноти простору Rm візьмемо довільну фундаментальну послідовність {x(n)}:

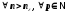 .
.
Із цієї нерівності одержуємо
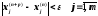 ,
,
 .
.
Тому
кожна послідовність
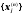 є фундаментальною в R,
за критерієм Коші в R
ця послідовність збіжна. Тому
є фундаментальною в R,
за критерієм Коші в R
ця послідовність збіжна. Тому
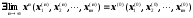
Rm
.
Rm
.
Тим
самим, довели, що евклідів простір Rm
повний за нормою
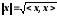 ,
цей простір є гільбертовим простором.
,
цей простір є гільбертовим простором.
Приклад Гільбертів простір l2 сумовних з квадратом послідовностей дійсних чисел
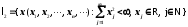 .
.
Довести, що цей простір є повним за нормою.
Скалярний добуток в l2 визначається
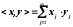 .
.
Якщо в нерівності Коші-Буняковського
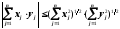
перейти до границі при n , то одержимо нерівність Коші-Буняковського для рядів
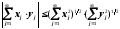
або
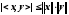 .
.
Звідси довели, що збігається ряд
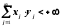 .
.
Тому l2-простір є евклідів простір. Він породжує норму
 =
=
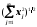 .
.
Візьмемо
фундаментальну послідовність
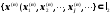 :
:
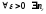 :
:
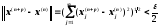 (* )
(* )
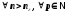 .
.
Із нерівності

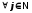
одержуємо,
що
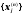 –
фундаментальна в R
для
кожного фіксованого
j
N.
За критерієм Коші в R
існує
границя
–
фундаментальна в R
для
кожного фіксованого
j
N.
За критерієм Коші в R
існує
границя
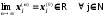 .
.
Розглянемо
послідовність
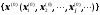 .
Покажемо, що
.
Покажемо, що
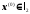 і
і
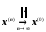 .
.
Із нерівності (*) одержуємо для будь-якого скінченного числа m доданків, що виконується нерівність
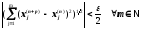 .
.
В цій нерівності перейдемо до границі при p і n > n , одержимо
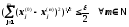 .
.
Тепер, спрямувавши m , знайдемо
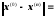
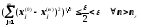 .
.
Це
означає, що
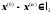 ,
тому
,
тому
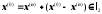 за лінійністю простору
за лінійністю простору
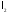 , крім того,
, крім того,
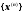 збіжна за нормою до
збіжна за нормою до
 при
n
.
при
n
.
Показали,
що довільна фундаментальна послідовність
в
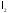 збіжна до елемента з цього простору,
тому простір
збіжна до елемента з цього простору,
тому простір
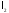 повний.
повний.
Евклідів
простір
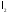 повний за нормою, породженою скалярним
добутком в
повний за нормою, породженою скалярним
добутком в
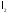 . Цей простір
. Цей простір
 є
гільбертовим простором.
є
гільбертовим простором.
Подібно
до того, як
 околом точки
околом точки
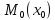 на координатній прямій R
ми називали множину
на координатній прямій R
ми називали множину
(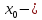
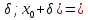
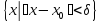 ,
,
тобто
інтервал з центром у точці
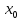 довжини 2
довжини 2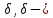 околом
точки
околом
точки
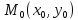 на
координатній площині будемо називати
множину
на
координатній площині будемо називати
множину
B :=
:=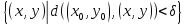 ,
,
тобто
множину точок
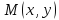 відкритого круга з центром у точці
відкритого круга з центром у точці
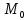 радіуса
радіуса
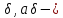 околом
точки
околом
точки
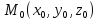 у координатному просторі
у координатному просторі
 множину
множину
B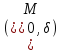 :=
:=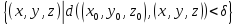
тобто
множину точок
 відкритої кулі з центром у точці
відкритої кулі з центром у точці
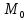 радіуса
радіуса
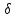 .
Взагалі множину B(
.
Взагалі множину B(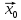 ,
r)
=
,
r)
=
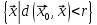 будемо
називати кулею з центром у точці
будемо
називати кулею з центром у точці
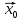 радіуса
радіуса
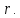
Подальший
виклад стосується відразу обох просторів.
Нехай маємо множину G
точок не будемо уточнювати чи вона
підмножина множини
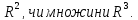 Точку
Точку
 будемо називати внутрішньою
точкою множини
G,
якщо існує окіл
будемо називати внутрішньою
точкою множини
G,
якщо існує окіл
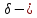 окіл
цієї точки, який включається в G.
Якщо всі точки множини є внутрішніми,
то її називають відкритою
і,
як правило, позначають
літерою
G.
окіл
цієї точки, який включається в G.
Якщо всі точки множини є внутрішніми,
то її називають відкритою
і,
як правило, позначають
літерою
G.
Множину точок
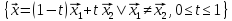
називають
відрізком,
кінцями
якого є точки
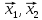 ,
а сукупність відрізків, кінцями яких
,
а сукупність відрізків, кінцями яких
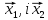 ,
,
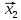 і
і
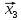 ,
…,
,
…,
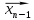 і
і
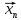 називають ламаною,
що сполучає точки
називають ламаною,
що сполучає точки
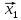 і
і
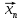 .
Якщо для будь
.
Якщо для будь
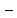 яких двох точок множини G
існує ламана, яка сполучає ці точки, і
кожна точка якої належить G,
то множина G
називається зв’язною.
Непорожня множина називається областю
(чи на площині, чи у просторі), якщо вона
відкрита і зв’язна. Точка
яких двох точок множини G
існує ламана, яка сполучає ці точки, і
кожна точка якої належить G,
то множина G
називається зв’язною.
Непорожня множина називається областю
(чи на площині, чи у просторі), якщо вона
відкрита і зв’язна. Точка
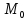 називається межовою
для області D,
якщо в будь
називається межовою
для області D,
якщо в будь
 якому
околі точки
якому
околі точки
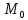 є точки, які належать D,
і точки, які D
не належать. Множину всіх межових точок
області D
називають її межею
і
позначають δD.
є точки, які належать D,
і точки, які D
не належать. Множину всіх межових точок
області D
називають її межею
і
позначають δD.
Як ілюстрацію розглянемо на координатній площині множину
E
= {(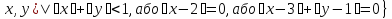
Множина
Е не є відкритою, однак її підмножина G
= {( є відкритою і зв'язною, тобто є областю.
Межею області G
є множина δG
= ={(
є відкритою і зв'язною, тобто є областю.
Межею області G
є множина δG
= ={( .
Межею множини Е є множина δЕ
={(
.
Межею множини Е є множина δЕ
={( ,
або
,
або
 .
.
У подальшому межею області на координатній площині буде крива, тобто множина точок площини, координати яких задовольняють рівняння
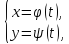
де
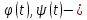 неперервні
на відрізку [
неперервні
на відрізку [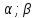 ]
функції. Такий спосіб задання кривої
носить назву параметричного.
Так, наприклад, відрізок з кінцями у
точках
]
функції. Такий спосіб задання кривої
носить назву параметричного.
Так, наприклад, відрізок з кінцями у
точках
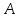 (
(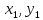 )
і B
)
і B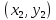 задається параметрично так
задається параметрично так
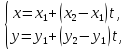
де
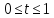 ,
а коло з центром у точці
,
а коло з центром у точці
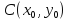 радіуса r
рівнянням
радіуса r
рівнянням
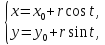
де
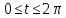 .
.
Кривою у просторі є множина точок простору, координати яких задовольняють рівняння
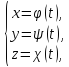
де
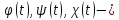 неперервні на відрізку [
неперервні на відрізку [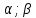 ]
функції. Як приклад, множина точок,
координати яких задовольняють рівняння
]
функції. Як приклад, множина точок,
координати яких задовольняють рівняння

де
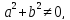
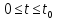 ,
є
крива, яку називають гвинтовою лінією.
,
є
крива, яку називають гвинтовою лінією.
При
аналітичному підході будь
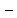 яка
фігура у просторі з обраною системою
координат задається рівняннями або
нерівністю (або їх системою), яке (які)
задовольняють координати кожної точки,
що належать фігурі, і не задовольняють
координати жодної точки, які не належать
цій фігурі, зокрема рівняння
яка
фігура у просторі з обраною системою
координат задається рівняннями або
нерівністю (або їх системою), яке (які)
задовольняють координати кожної точки,
що належать фігурі, і не задовольняють
координати жодної точки, які не належать
цій фігурі, зокрема рівняння
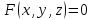
задає у просторі поверхню. Поверхня може бути задана параметрично, але це потребує функцій двох змінних.
Топологічні
властивості просторів
 і
і
Серед
властивостей збіжних послідовностей
особлива роль за теоремою Больцано
 Вейєрштасса
та критерієм Коші. Якраз через ці теореми
розкривається повнота просторів
Вейєрштасса
та критерієм Коші. Якраз через ці теореми
розкривається повнота просторів
 .
Щодо техніки введення понять, то будемо
виходити з того, що означення границі
числової послідовності (
.
Щодо техніки введення понять, то будемо
виходити з того, що означення границі
числової послідовності (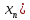 .
.
,,
 ҆ ҆
҆ ҆
можна перефразувати у такий спосіб:
,,Точка
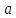 метричного простору R
називається
границею числової послідовності (
метричного простору R
називається
границею числової послідовності ( точок цього простору, якщо для будь
точок цього простору, якщо для будь
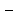 якого
якого
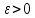 існує номер
існує номер
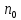 такий, що всіх
такий, що всіх
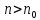 виконується нерівність
виконується нерівність
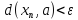 ҆
҆,
҆
҆,
тобто
означення границі числової послідовності
формується тільки через поняття відстані,
а отже, його можна перенести у довільний
метричний простір, зокрема в
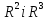 .
Отож будемо діяти за схемою: означимо
поняття точок простору
.
Отож будемо діяти за схемою: означимо
поняття точок простору
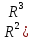 ),
виділимо клас збіжних послідовностей
і перенесемо на них всі ті властивості
числових послідовностей, у формулюванні
яких фігурує тільки відстань.
),
виділимо клас збіжних послідовностей
і перенесемо на них всі ті властивості
числових послідовностей, у формулюванні
яких фігурує тільки відстань.
Означення
. Відповідність,
яка кожному натуральному числу відносить
точку
простору
 )
називається послідовністю точок цього
простору
і
позначається (
)
називається послідовністю точок цього
простору
і
позначається ( )
або
)
або
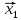 ,
,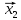 ,…,
,…,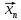 ,…
.
,…
.
Зрозуміло,
що в залежності від того, послідовність
точок якого простору розглядається
маємо ще й такий запис послідовностей
(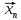 )
= ((
)
= ((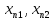 )),
(
)),
(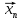 )
= ((
)
= (( )).
)).
В
очевидний спосіб переносимо поняття
обмеженої послідовності, а саме
послідовність ( )
обмежена,
якщо існує куля, якій належать всі точки
цієї послідовності.
)
обмежена,
якщо існує куля, якій належать всі точки
цієї послідовності.
Означення
. Точка
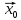 простору
простору
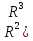 )
називається границею послідовності
(
)
називається границею послідовності
(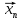 ),
якщо для
),
якщо для
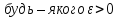 існує номер
існує номер
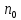 такий, що всіх
такий, що всіх
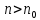 виконується нерівність
виконується нерівність
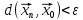 .
.
Про послідовність, яка має границю, кажуть, що вона збігається (є збіжною), і за границею залишається стандартне позначення
