
- •Общие методические указания
- •Физические основы механики
- •Тема 1.5. Элементы релятивистской динамики
- •Тема 1.6. Физика колебаний и волн
- •2. Статистическая физика и термодинамика
- •Тема 2.1. Молекулярно - кинетическая теория
- •Тема 2.2. Основы термодинамики
- •Тема 2.3. Статистические распределения
- •Электричество и магнетизм Тема 3.1. Электростатика
- •Тема 3.2. Постоянный электрический ток
- •Тема 3.3. Магнитные поле
- •Тема 3.4. Электромагнитное поле
- •5. Квантовая физика
- •Тема 5.9. Элементы квантовой электроники
- •Тема 5.10. Фазовые равновесия и фазовые превращения
- •6. Состояние вещества
- •Тема 6.1. Вещество в различных условиях
- •7. Современная физическая картина мира
- •Список литературы
- •Контрольная работа №1
- •Учебные материалы по разделам курса физики
- •Основные формулы
- •Примеры решения задач
Примеры решения задач
Пример 1.
Уравнение движения материальной точки вдоль оси имеет вид x = A+Bt+Ct3, где А = 2 м, В = 1 м/с, С = 0,5 м/с3. Найти коорди- нату х, скорость х и ускорение ах точки в момент времени t = 2 c.
|
Дано: А = 2 м; В = 1 м/с; С = 0,5 м/с3; t = 2 c. |
Решение:
Координату х найдем, подставив в уравнение движения числовые значения коэффициентов А, В и С и времени t: x = ( 2 + 12 0,523 ) м = 0. Мгновенная скорость относительно оси х есть первая производная от координаты по времени: |
|
х, х , ах ? |
![]() .
.
Ускорение точки найдем, взяв первую производную от скорости по времени:
![]() .
.
В момент времени t = 2 c
x = ( 1 30,522 ) м/с = 5 м/с;
ах = 6 (0,5)2 м/с2 = 6 м/с2.
Пример 2.
Тело вращается вокруг неподвижной оси по закону = A+Bt+Ct2, где А = 10 рад, В = 20 рад/с, С = 2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии r = 0,1 м от оси вращения, для момента времени t = 4 c.
|
Дано: А = 10 рад В = 20 рад/с С = 2 рад/с2 t = 4 c r = 0,1 м |
Решение:
Полное
ускорение точки
|
|
а ? |
.Так
как векторы
![]() и
и
![]() взаимно
перпендикулярны, то модуль ускорения
взаимно
перпендикулярны, то модуль ускорения
|
Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами
где – модуль угловой скорости тела; – модуль его углового ускорения. |
О •
Рис. 1
|
|
Подставляя
выражения
![]() и
и
![]() в
формулу
(1),
находим:
в
формулу
(1),
находим:
![]() .
(2)
.
(2)
Угловую скорость найдем, взяв первую производную угла поворота по времени:
![]() .
.
В момент времени t=2c модуль угловой скорости
= [ 20 + 2(2)4 ] рад/с = 4 рад/с.
Угловое ускорение найдем, взяв первую производную угловой скорости по времени:
![]() рад/с2.
рад/с2.
Подставляя значения , и r в формулу (2), получаем
![]() .
.
Пример 3.
Два
шарика массами m1
и m2
движутся
навстречу друг другу по идеально гладкой
поверхности со скоростями
![]() и
и
![]() .
Определить скорость шариков после
абсолютно неупругого удара.
.
Определить скорость шариков после
абсолютно неупругого удара.
|
Дано: m1 m2
|
Решение: На шарики действует сила тяжести и сила нормальной реакции, взаимно уравновешивающие друг друга, в направлении оси x внешние силы отсутствуют. Поэтому сохраняется импульс в данном направлении
где
|
|
|
после взаимодействия. В проекциях:
|
m1
x
|
x
Рис. 2 |
![]() .
.
Отсюда
![]() .
.
Пример 4.
Человек стоит на неподвижной тележке и бросает горизонтально камень массой m1 = 8 кг со скоростью 1 = 5 м/с. Определить, какую работу совершает человек, если масса человека вместе с тележкой равна m2 = 160 кг.
|
Дано: m1 = 8 кг m2 = 160 кг 1 = 5 м/c
|
Решение:
Работа,
совершаемая человеком в момент броска,
равна изменению механической энергии
системы “
человек + тележка + камень ”:
А
= W.
В силу того, что система до броска
покоилась, W1
= 0 и
|
|
A ? |
где 2 – скорость тележки с человеком сразу после броска.
По закону сохранения импульса m11 = m22 , откуда
![]() .
(2)
.
(2)
Следовательно,
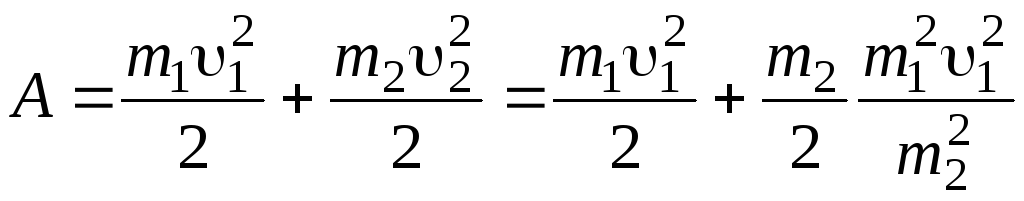 .
(3)
.
(3)
Подставляя значения m1, m2, 1 , 2 в формулу (3), найдем
![]() .
.
Пример 5.
Шар массой m1, движущийся горизонтально с некоторой скоростью 1, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю своей кинетической энергии первый шар передал второму?
|
Дано:
m1 m2 1
|
Решение:
Доля энергии, переданной первым шаром второму, выразится соотношением
где
|
|
? |
Как
видно из формулы (1), для определения надо найти![]() .
Согласно условию задачи, импульс системы
двух шаров относительно горизонтального
направления не изменяется и механическая
энергия шаров в другие виды не переходит.
Пользуясь этим, найдем:
.
Согласно условию задачи, импульс системы
двух шаров относительно горизонтального
направления не изменяется и механическая
энергия шаров в другие виды не переходит.
Пользуясь этим, найдем:
![]() ;
(2)
;
(2)
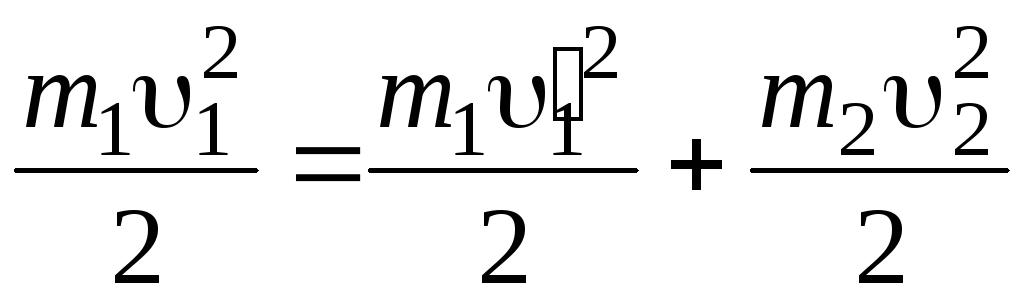 .
(3)
.
(3)
Решим совместно уравнения (2) и (3)
![]() .
.
Подставив
это выражение
![]() в формулу (1) и сократив на1
и m1,
получим
в формулу (1) и сократив на1
и m1,
получим
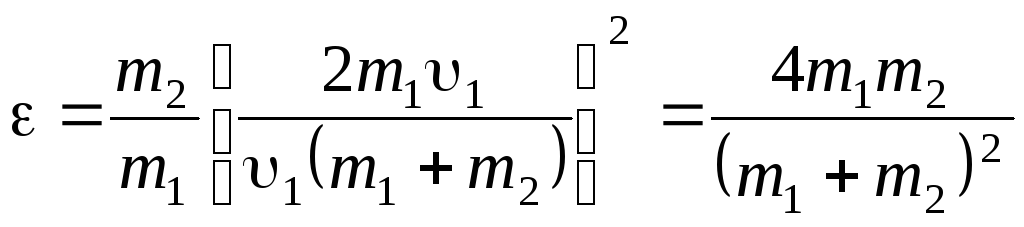 .
.
Из найденного соотношения видно, что доля переданной энергии зависит только от массы сталкивающихся шаров.
Пример 6.
Определить работу А внешней силы при растяжении двух пружин жесткостьюk1 = 200 H/м и k2 = 350 H/м соединенных последовательно, если суммарное удлинение пружин Δl = 4 см.
|
Дано:
k1 = 200 H/м k2 = 350 H/м Δl = x0 =0,04 м |
Решение: При последовательном соединении пружин, силы действующие на первую и вторую пружины одинаковы F1 = F2 = F, а суммарное удлинение пружин |
|
A ? |
x = x1 + x2 , (1)
где x1 – удлинение первой пружины, x2 – удлинение второй пружины.
Согласно закону Гука F1 = - k1 x1 , иF2 = - k2 x2 ,откуда
![]()
Подставляя значение x1 и x2 в уравнение (1) получим:
![]() (2)
(2)
При малой деформации dx работа внешней силы равна
dA = F dx (3)
Полную работу внешней силы при деформации пружины найдем проинтегрировав выражение (3) от от 0 доx0 , учитывая при этом, что внешняя сила направлена в сторону противоположную силе Гука (Fвнеш. = -F );
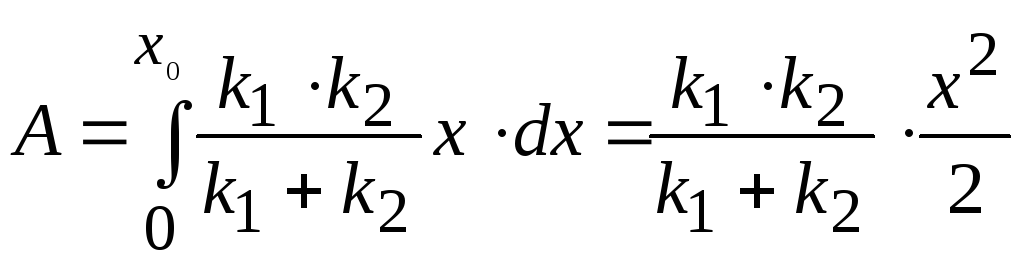 .
(4)
.
(4)
Проверим размерность:
![]() .
.
Убедившись, что полученная единица является единицей работы (Дж), подставим в формулу (4) значения величин и произведем вычисления:
![]() .
.
Пример 7.
При выстреле из пружинного пистолета вертикально вверх пуля массой m = 20 г поднялась на высоту h = 5 м. Определить жесткость k пружины пистолета, если она была сжата на х = 10 см. Массой пружины и силами трения пренебречь.
|
Дано: m =0,02 кг h = 5 м х =0,1м |
Решение: Рассмотрим систему пружина – пуля. Так как на тело системы действуют только консервативные силы, то для решения задачи можно применить закон сохранения энергии в механике. |
|
k ? |
Согласно ему полная механическая энергия Е1 системы в начальном состоянии (в данном случае перед выстрелом) равна полной энергии Е2 в конечном состоянии (когда пуля поднялась на высоту h), т. е.
Е1 = Е2, или Т1 + П1 = Т2 + П2, (1)
где Т1, Т2, П1 и П2 – кинетические и потенциальные энергии системы в начальном и конечном состоянии.
Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид
П1 = П2. (2)
Примем потенциальную энергию пули в поле сил тяготения Земли, когда пуля покоится на сжатой пружине, равной нулю, а высоту подъема пули будем отсчитывать от торца сжатой пружины. Тогда энергия системы в начальном состоянии будет равна потенциальной энергии сжатой пружины, т. е. П1 = ½ kx2, а в конечном состоянии – потенциальной энергии пули на высоте h, т. е.
П2 = mgh.
Подставив выражения П1 и П2 в формулу (2), найдем
½ kx2 = mgh,
откуда k = 2mgh/x2. (3)
Проверим, дает ли полученная формула единицу жесткости k. Для этого в правую часть формулы (3) вместо величин подставим их единицы:
![]() .
.
Убедившись, что полученная единица является единицей жесткости (1 Н/м), подставим в формулу (3) значения величин и произведем вычисления:
![]()
Пример 8.
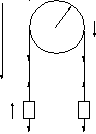
Через блок в виде сплошного диска, имеющего массу m =0,08 кг (рис. 3), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m1 =0,1 кг и m2 =0,2 кг. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь.
|
Дано: m =0,08 кг m1 = 0,1 кг m2 = 0,2 кг |
Решение: Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действуют две силы: сила тяжести и сила упругости (сила натяжения нити). Направим ось х вертикально вниз и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось. |
|
а ? |
Для первого груза
![]() ;
(1)
;
(1)
для второго груза
![]() .
(2)
.
(2)
Под действием моментов сил
![]() и
и![]() относительно осиz,
перпен- дикулярной плоскости чертежа
и направленной за чертеж, блок приобретает
угловое ускорение.
Согласно основному уравнению
относительно осиz,
перпен- дикулярной плоскости чертежа
и направленной за чертеж, блок приобретает
угловое ускорение.
Согласно основному уравнению
|
r
x
Т1 Т2
m1 g m2 g
Рис. 3 |
динамики
вращательного движения,
где
Согласно третьему закону Нью- тона,
с учетом невесомости нити
|
( m2g – m2a ) r – ( m1g + m1a ) r = m r2a / ( 2 r ).
После сокращения на r и перегруппировки членов найдем:
![]() (4)
(4)
После подстановки числовых значений получим:
![]() .
.
Пример 9.
Маховик в виде сплошного диска радиусом R = 0,2 м и массой m = 50 кг раскручен до частоты вращения n1 = 480 об/мин и предоставлен сам себе. Под действием силы трения маховик остановился через t = 50 с. Найти момент M сил трения.
|
Дано:
R = 0,2 м m = 50 кг n1=480 об/мин t = 50 с |
Решение:
Для решения
задачи воспользуемся основным
уравнением динамики вращательного
движения в виде:
где
|
|
М ? |
оси
z,
совпадающей с геометрической осью махо-
вика, за интервал времени dt
;
![]() -момент
внешних сил (в данном
-момент
внешних сил (в данном
случае момент сил трения), действующих на маховик относительно оси z.
Момент
сил трения можно считать не изменяющимся
с течением времени (![]() =const),
поэтому интегрирование уравнения (1)
приводит к выражению:
=const),
поэтому интегрирование уравнения (1)
приводит к выражению:
![]() ,
(2)
,
(2)
При вращении твердого тела относительно неподвижной оси изменение проекции момента импульса
![]() ,
(3)
,
(3)
где
Jz
– момент
инерции маховика относительно оси z;
![]() -изменение
угловой скорости маховика.
-изменение
угловой скорости маховика.
Приравнивая
правые части равенства (2) и (3), получим
![]() ,
откуда
,
откуда
![]() .
(4)
.
(4)
Момент инерции маховика в виде сплошного диска определяется по формуле
![]() .
.
Изменение
угловой скорости
![]() выразим через конечнуюn2
и начальную
n1
частоты
вращения, пользуясь соотношением
выразим через конечнуюn2
и начальную
n1
частоты
вращения, пользуясь соотношением
![]()
![]() .
.
Подставив
в формулу (4) выражение Jz
и
![]() ,
получим
,
получим![]() .
(5)
.
(5)
Проверим, дает ли расчетная формула единицу момента силы (Н·м). Для этого в правую часть формулы вместо символов величин подставим их единицы:
![]() .
.
Подставим в (5) числовые значения величин и произведем вычисления , учитывая, что n1=480 об/мин = 8 об/с;
![]()
Знак минус показывает, что момент сил трения оказывает на маховик тормозящее действие.
Пример 10.
Платформа в виде сплошного диска радиусом R = 1,5 м и массой m1 = 180 кг вращается около вертикальной оси с частотой n=10 об/мин. В центре платформы стоит человек массой m2 = 60 кг. Какую линейную скорость v относительно пола помещения будет иметь человек, если он перейдет на край платформы ?
|
Дано:
R = 1,5 м m1 = 180 кг m2 = 60 кг n=10 об/мин |
Решение: Согласно условию задачи, момент внешних сил относительно оси вращения z , совпадающей с геометрической осью платформы, можно считать равным нулю. При этом условии проекция Lz момента импульса системы платформа – человек остается постоянной:
|
|
v ? |
где J – момент инерции платформы с человеком от-
носительно
оси
z
;
![]() -угловая
скорость платформы.
-угловая
скорость платформы.
Момент инерции системы равен сумме
моментов инерции тел, входящих в состав
системы, поэтому в начальном состоянии
J=J1+J2
, а в конечном
состоянии![]()
С учетом этого, равенства (1) примет вид
![]() (2)
(2)
где
значения моментов инерции J1
и J2
платформы
и человека соответственно относятся к
начальному состоянию системы;
![]()
![]() -
к конечному.
-
к конечному.
Момент инерции платформы относительно оси z при перехо-
де
человека не изменяется:
![]() Момент инерции человека относительно
той же оси будет изменяться. Если
рассматривать человека как материальную
точку, то его момент инерцииJ2
в начальном
состоянии (в центре платформы) можно
считать равным нулю. В конечном состоянии
(на краю платформы) момент инерции
человека
Момент инерции человека относительно
той же оси будет изменяться. Если
рассматривать человека как материальную
точку, то его момент инерцииJ2
в начальном
состоянии (в центре платформы) можно
считать равным нулю. В конечном состоянии
(на краю платформы) момент инерции
человека
![]()
Подставим
в формулу (2) выражения моментов инерции,
начальной угловой скорости вращения
платформы с человеком (![]() )
и конечной угловой скорости (
)
и конечной угловой скорости (![]() v/R,
где v
–
скорость человека относительно пола):
v/R,
где v
–
скорость человека относительно пола):
![]() v/R.
v/R.
После сокращения на R2 и простых преобразований находим скорость:
v
=
![]() .
.
v
=
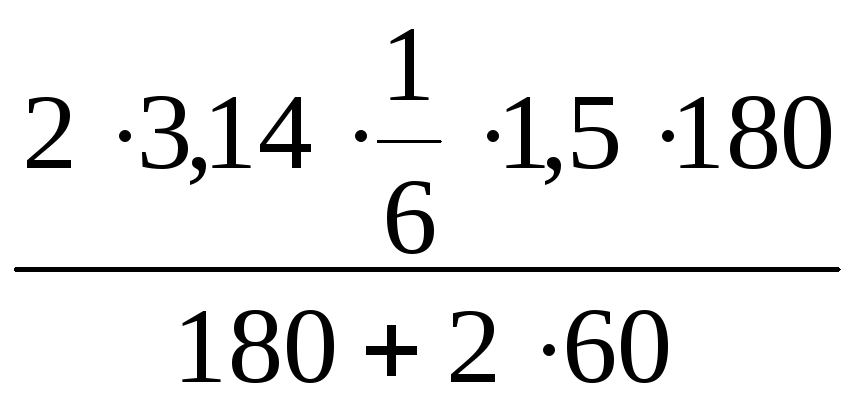 м/с = 1
м/с.
м/с = 1
м/с.
Пример 11.
Материальная точка массой m = 5 г совершает гармонические колебания с частотойv = 0,5 сек-1.Амплитуда колебаний А = 3 см. Определить: 1) скорость υ точки в момент времени , когда смещениеx = 1,5 см;2) максимальную силуFмакс, действующую на точку; 3) полную энергиюE колеблющейся точки.
|
Дано: m = 0,005 кг v = 0,5 сек-1 А = 0,03 м x =0,015 м |
Решение:
x = Asin (ωt + φ) (1) где x – смещение колеблющейся точки от по- ложения равновесия,А –амплитуда,ωt + φ – фаза колебания, φ – начальная фаза, ω- циклическая частота, t – время. |
|
υ, Fмакс ,Е ? |
Формулу скорости получим, взяв первую производную от смещения по времени,
![]() (2)
(2)
Чтобы выразить скорость через смещение, надо исключить из (1) и (2) время. Для этого возведем оба уравнения в квадрат и сложим:
![]() .
.
Решив последнее уравнение относительно υ , найдем
![]() (3)
(3)
Подставив в это выражение числовые значения величин, получим:
![]()
Знак "плюс"соответствует случаю, когда направление скорости совпадает с положительным направлением осиx. Знак"минус "соответствует случаю, когда направление скорости совпадает с отрицательным направлением осиx.
2) Силу, действующую на точку, найдем по второму закону Ньютона:
![]() ,
(4)
,
(4)
где а – ускорение точки, которое получим, если возьмем производную по скорости от времени:
![]()
или
![]()
Подставив выражение для ускорение в (4), будем иметь:
![]()
![]()
Отсюда получим максимальное значение силы
![]()
![]()
Подставив в это уравнение числовые значения величин, найдем
![]()
3) Полная энергия колеблющейся точки есть сумма кинети- ческой и потенциальной энергий, вычисленных для любого момента времени. Проще всего вычислить полную энергию в момент, когда кинетическая энергия достигает максимального значения. В это время потенциальная энергия равна нулю. Поэтому полная энергия Еколеблющейся точки равна максимальной кинетической энергииТмакс и может быть определена по формуле
![]() (5)
(5)
Максимальную скорость можно определить
по формуле (2), если принять
![]()
![]()
Подставив это выражение скорости в (5), найдем
![]()
После подстановки числовых значений получим
![]()
Пример 12.
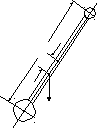
На концах тонкого стержня длиной l = 30 см и массойmст= 400 г укреплены грузики массойm1 = 200 гиm2 = 300 г . Стержень колеблется около горизонтальной оси, проходящей через его середину ( рис. 4). Определить периодТ колебаний, совершаемых стержнем.
|
Дано:
l =0, 3 м mст= 0,4 кг m1 = 0,2 кг m2 = 0,3 кг
|
Решение: Период колебания физического маятника, каким является стержень, определяется по формуле
где J – момент инерции маятника, m – масса маятника,а –расстояние от центра тяжести (центра масс) маятника до оси.
|
|
Т - ? |
Момент инерции физического
|
маятника
J – состоит из
моментов инерции
Пренебрегая размерами грузиков, получим
Момент инерции стержня относитель- но оси, проходящей через его середи- ну, определяется по формуле
|
m1
l а • О • mg
m2
Рис. 4 |
![]()
Общий момент инерции физического маятника равен
![]()
Вынеся за скобку множитель![]() ,
получим
,
получим
![]() (2)
(2)
Подставив в (4) числовые значения, получим
![]()
Масса физического маятника состоит из массы стержня и массы грузиков
![]()
Для определения расстояния а центра тяжести маятника от оси вращения напишем условие равновесия стержня с грузиками, находящегося в горизонтальном положении, относительно центра тяжести
![]()
Сократив это равенство на g и, решив его относительноа, получим
![]()
Подставим числовые значения
![]()
Теперь можем найти период колебаний, подставив числовые значения величин в (1)
![]()
Пример 13.
Складываются два колебания одинакового направления, выра- женные уравнениями
![]()
где А1=3 см, А2=2 см, τ1=1/6 с, τ2=1/3 с, Т=2 с. Построить векторную диаграмму сложения этих колебаний и написать уравнение результирующего колебания.
|
Дано:
А1=0,03 м А2=0,02 м τ1=1/6 с Т=2 с |
Решение:
Для построения
векторной диаграммы сложения двух
колебаний одного направления надо
фиксировать какой-либо момент времени.
Обычно векторную диаграмму строят
для момента времени t =
0. Преобразовав оба уравнения к
канонической форме |
|
x-? |
![]()
Отсюда видно, что оба складываемых гармонических колебания имеют одинаковую циклическую частоту
![]() .
.
Начальные фазы первого и второго колебаний соответственно равны
![]()
Произведем вычисления:
![]()
![]()
Изобразим векторы
![]() и
и![]() .
Для этого отложим отрезки длинойА1=0,03
миА2=0,02 мпод угламиφ1=300иφ2=600к оси Ох. Результирующее колебание
будет происходить с той же частотой ω
и амплитудойА, равной геометрической
сумме амплитуд
.
Для этого отложим отрезки длинойА1=0,03
миА2=0,02 мпод угламиφ1=300иφ2=600к оси Ох. Результирующее колебание
будет происходить с той же частотой ω
и амплитудойА, равной геометрической
сумме амплитуд![]() и
и![]() :
:![]() .
Согласно теореме косинусов,
.
Согласно теореме косинусов,
![]()
Начальную фазу результирующего колебания можно также определить непосредственно из векторной диаграммы (рис. 5)
![]()
Произведем вычисления
![]()
![]()
|
y
φ2
φ φ1 x A1cosφ1+A2cosφ2
Рис. 5
|
или φ = 0,735 рад.
Так как результирующее колеба- ние является гармоническим, имеет ту же частоту, что и слагаемые колебания, то его можно записать в виде:
где А = 0,048м, ω = 3,14с-1, φ = 0,735 рад. |
Пример 14.
Плоская волна распространяется вдоль прямой со скоростью υ = 20м/с.Две точки, находящиеся на этой прямой на расстояния х1 = 12 м их2= 15 мот источника волн, колеблются с разностью фаз
∆φ = 0,75π.Найти длину волныλ,написать уравнение волны и найти смещение указанных точек в моментt = 1,2 с, если амплитуда колебанийA = 0,1 м.
|
Дано:
υ = 20м/с х1 = 12 м х2= 15 м ∆φ = 0,75π t = 1,2 с A = 0,1 м |
Решение:
Точки, находящиеся друг от друга на расстоянии, равном длине волны λ, колеблются с разностью фаз, равной 2π; точки, находящиеся друг от друга на любом расстоянии Δх, колеблются с разностью фаз, равной
Решая это равенство относитедьно λ , получаем
|
|
λ - ? |
Подставив числовые значения величин, входящих в выражение (1), и выполнив арифметические действия, получим
![]()
Для
того, чтобы написать уравнение плоской
волны надо еще найти циклическую частоту
ω.
Так как
![]() - период колебаний), то
- период колебаний), то
![]() .
.
Произведем вычисления
![]()
Зная амплитуду А колебаний, циклическую частоту ω и скорость υ распространения волны, можно написать уравнение плоской волны для случая
![]() (2)
(2)
где А=0,1 м, ω =5π с-1, υ=20 м/с.
Чтобы найти смещение y указанных точек, достаточно в уравнение (2) подставить значенияt и x
![]()
![]()


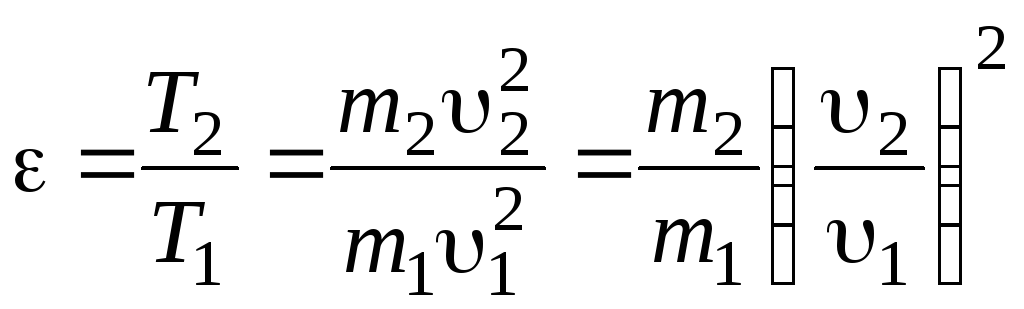 ,
(1)
,
(1)
 J1
иJ2
обоих грузиков и момента инерцииJ3
стержня
J1
иJ2
обоих грузиков и момента инерцииJ3
стержня