Пример решения задач

На рисунке представлена схема нагружения двухопорной балки.

Н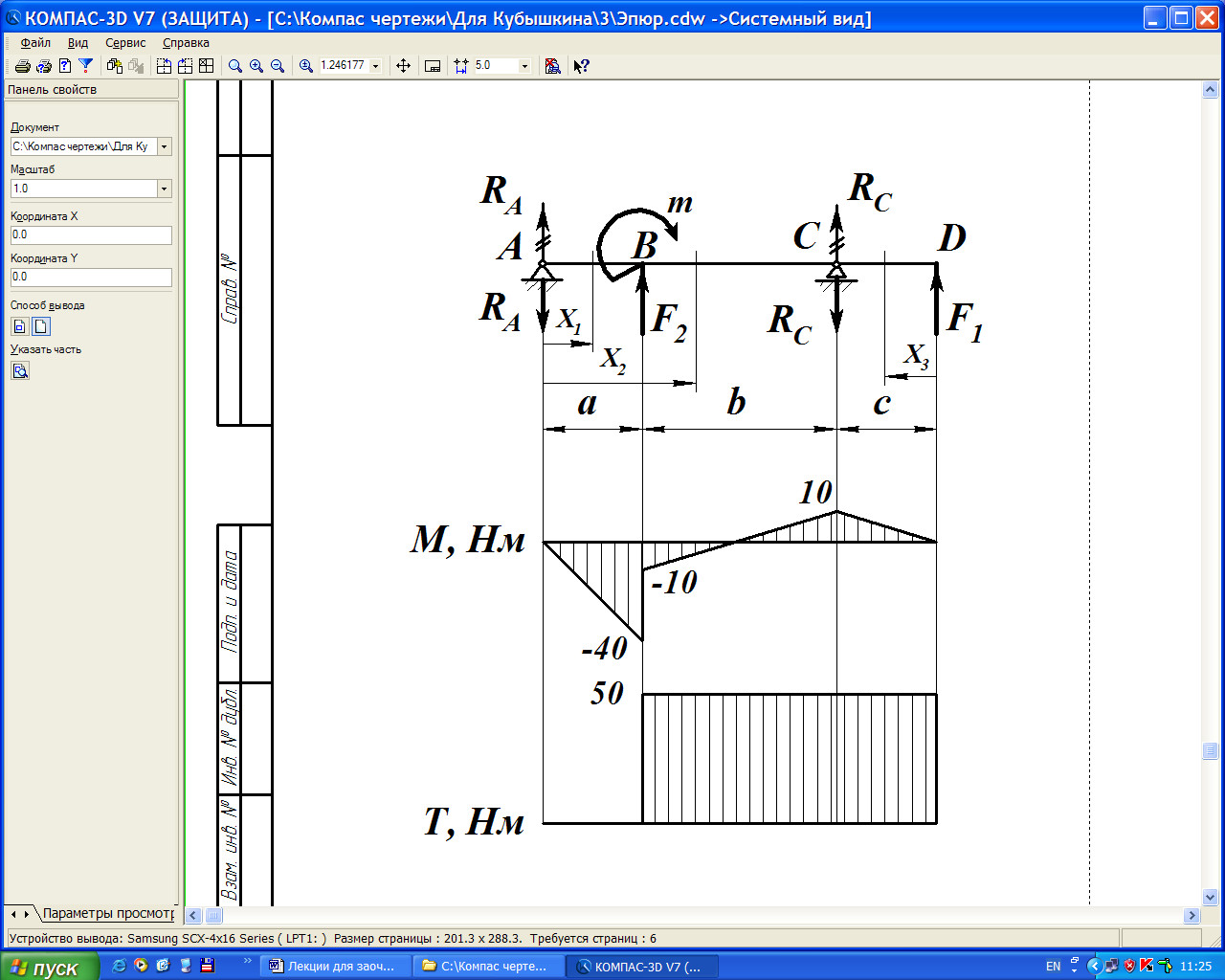агрузки:

радиальные силы

,,

изгибающий момент m = 30 Нм,

Размеры участков:

а = с = 0,1м, b = 0,2м

Решение.

Пример оформления

эпюр изгибающих Ммоментов для двухопорной балки

Изобразим на силовой схеме

предположительное направление реакций опор и- вверх.

Определим величину и направление реакций и, используя уравнения равновесия плоской системы сил.

Составим уравнение моментов сил относительно опоры С,считая действие момента по направлению движения часовой стрелки положительным (со знаком «плюс»):

Знак «минус» свидетельствует о неправильно выбранном направлении . Меняем на схеме направлениена противоположное.

Реакция = 400 Н, направлена вниз.

Составим уравнение проекций всех сил на вертикальную ось Y, считая направление вектора вверх положительным (со знаком «плюс»):

Знак «минус» свидетельствует о неправильно выбранном направлении . Меняем на схеме направлениена противоположное.

Реакция = 200 Н, направлена вниз.

Проверяем правильность решения, используя дополнительное уравнение моментов сил относительно любой неопорной точки, например, точки В:

Полученный в результате вычислений «ноль» свидетельствует о правильности определения реакций икак по величине, так и по направлению.

Используя метод сечений построим эпюры изгибающего момента Ми крутящего моментаТ. Для этого выделяем на схеме три характерных участка:АВ,ВСиCD. Последовательно на каждом участке проводим произвольное поперечное сечение с координатойх. Мысленно отбрасываем одну из отсекаемых частей балки (правую или левую), составляем уравнения равновесия для оставшейся части.

Участок АВПроводим сечение с координатойх₁, изменяемой в пределах границ участка:(начало координат в точке А). Из условия равновесия рассматриваемой части длинойх₁составляем выражение для изгибающего моментаМ₁в сечении как алгебраическую сумму (с учетом правила знаков) моментов всех внешних сил, действующих на рассматриваемую часть относительно сечения:

График изменения изгибающего момента М₁представляет собой наклонную прямую. Знак «минус» соответствует выпуклому изгибу балки. Значение момента достаточно вычислить для двух сечений, соответствующих границам участкаАВ:

при

при Нм

Полученные координаты в выбранном масштабе отмечаем по эпюре М(положительные значения откладываем вверх от базовой линии эпюры, а отрицательные – вниз) и соединяем их прямой линией.

Участок ВСПроводим сечение с координатойх₂изменяемой в пределах участка(начало координат остается в точкеА). Для рассматриваемой части балки длинойх₂составляем выражение для изгибающего моментаМ₂:

График изменения изгибающего момента М₂является наклонной прямой. Вычислим значениеМ₂для граничных сечений участкаВС:

при

Нм;

при

Нм

По полученным координатам строим эпюру М на участке ВС.

Участок CDНа этом участке удобнее рассматривать правую отсеченную часть балки, мысленно отбрасывая левую часть. В этом случае выражение для М имеет более простой вид.

Проводим сечение с координатой х₃изменяемой в пределах участка(начало координат переносим в точкуD). Для рассматриваемой части балки длинойx₃составляем выражение для изгибающего моментаМ₃:

Вычисляем значения М₃для граничных сечений и строим эпюру на участкеCD:

при ,;

при ,Нм

По полученным координатам строим эпюру М на участке CD.

Учитывая, что по условию задачи на участке BD действует постоянный вращающий момент Т = 40 Нм, строим эпюру Т в виде прямой, параллельной базовой линии эпюры.

Из анализа эпюр М и Т следует, что наиболее нагруженным, а следовательно предположительно опасным с точки зрения прочности является сечение В. В этом сечении действуют одновременно наибольший изгибающий М = 40 Нм и крутящий Т = 50 Нм моменты.

Вычисляем приведенный (эквивалентный) момент М_пр в сечении В:

Нм

Определяем диаметр вала, удовлетворяющий условию статической прочности:

мм

где =85МПа – допускаемое напряжение для стали 45 с пределом прочности _В = 750 МПа.

Принимаем стандартное значение диаметра мм.

Для проверки вала на усталостную прочность определим следующие параметры:

- предел выносливости при симметричном цикле изгиба _-1 и кручения _-1:

МПа

МПа

- амплитудные _а, _а и средние _т, _т напряжения цикла, действующие в опасном сечении при изгибе и кручении:

МПа;

МПа

- эффективные коэффициенты концентрации напряжений при изгибе К_ и кручении К_:

К_ = 1, К_ = 1 – для сечений без концентраторов;

- масштабные коэффициенты при изгибе _ и кручении _:

- коэффициент шероховатости :

= 0,93 – для шлифованных поверхностей;

- коэффициенты асимметрии цикла при изгибе и кручении:

; - для стали 45.

- коэффициенты запаса усталостной прочности в сечении В при изгибе и кручении:

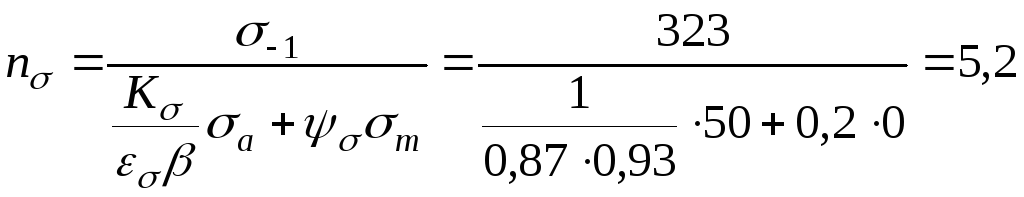
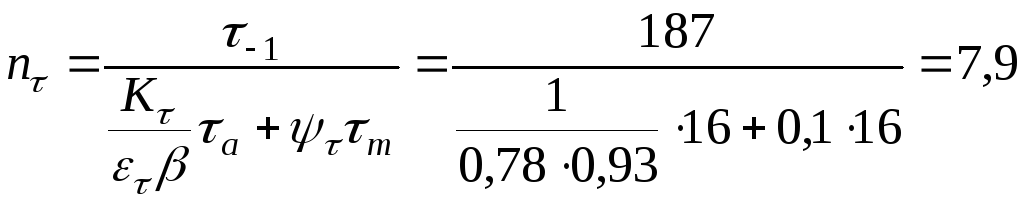
- коэффициент запаса усталостной прочности в опасном сечении:

Проверяем выполнение условия усталостной прочности вала:

Условие усталостной прочности выполняется, следовательно прочность вала обеспечена.