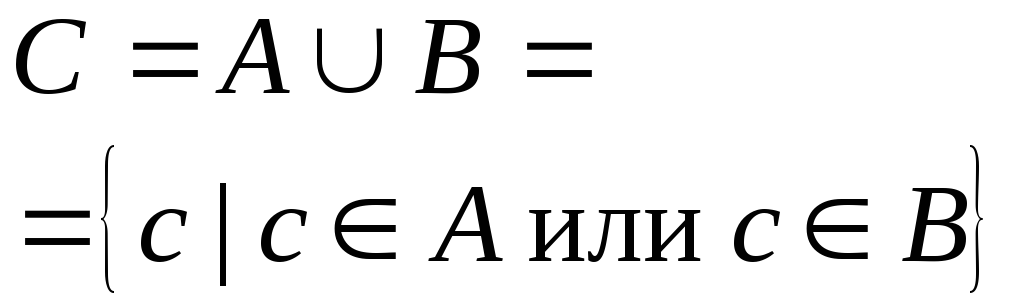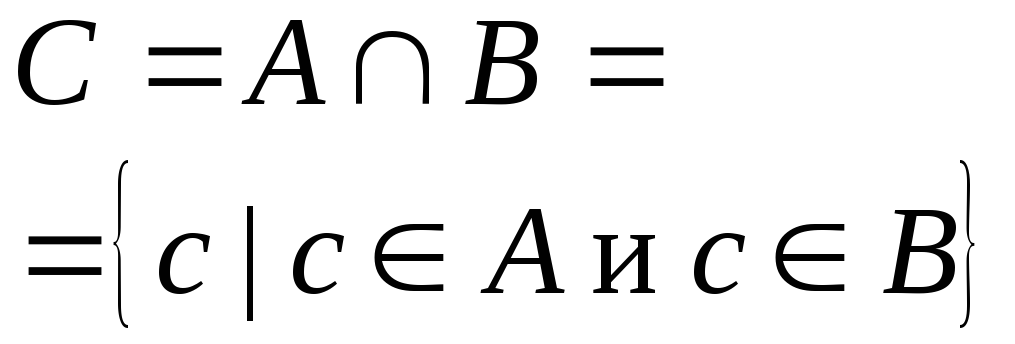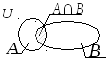МАТ_ ЛОГИКА / МАТЕМАТИЧЕСКАЯ ЛОГИКА_ЛК6_20_02_2012_Булевы алгебры

Булевы алгебры

Поставим в соответствие высказыванию логическую переменную х, которая принимает значение «1», если высказывание истинно, и «0», если высказывание ложно. Тогда каждая формула будет задавать логическую функцию – функцию от логических переменных , которая сама может принимать только два значения «1» или «0».

Функцией алгебры логики (логической функцией) называется произвольная n-местная функция, аргументы и значения которой принадлежат множеству {0, 1}.

Множество всех логических функций обозначается Р₂. Число всех возможных различающихся наборов значений n переменных логической функции равно 2ⁿ (равно числу всех возможных двоичных векторов длины n ). Тогда число всех различных функций n переменных равно – число возможных расстановок нулей и единиц в столбце с 2ⁿ строками.

Одна и та же логическая функция может быть задана формулами, включающими различные наборы логических операций. Например: . Существуют наборы логических операций, с помощью которых можно выразить любые другие логические функции. Такие наборы называются базисами. Наиболее хорошо изученным является базис .

Формулы, содержащие кроме переменных и скобок только знаки конъюнкции, дизъюнкции и отрицания, называются булевыми.

Теорема. Всякая логическая функция может быть представлена булевой формулой.

Из теоремы следует, что система операций функциональна полна.

Алгебра , основным множеством которой является множество Р₂ логических функций, а операциями – конъюнкция, дизъюнкция и отрицание, называется булевой алгеброй логических функций.

Всякая алгебра, содержащая две бинарные и одну унарную операции, называется булевой, если ее операции удовлетворяют соотношениям (1)–(15) таблицы.

Номер п/п	Название закона	Формула
1	Идемпотентность дизъюнкции
2	Идемпотентность конъюнкции
3	Коммутативность конъюнкции
4	Коммутативность дизъюнкции
5	Ассоциативность дизъюнкции
6	Ассоциативность конъюнкции
7	Дистрибутивность конъюнкции относительно дизъюнкции
8	Дистрибутивность дизъюнкции относительно конъюнкции
9	Правила де Моргана	;
10	Законы поглощения
11	Закон двойного отрицания
12	Свойства констант 0 и 1	; ;
13	Закон противоречия
14	Закон исключенного третьего
15	Закон импликации
16	Закон поглощения
17	Законы склеивания	;
18	Закон обобщенного склеивания
19	Закон ортогонализации
20	Формулы связи между логическими операциями	)

Операции и формулы булевой алгебры называются булевыми.

Примеры булевых алгебр:

– алгебра логических функций с операциями конъюнкции, дизъюнкции и отрицания;

– булева алгебра множеств над U с операциями объединения, пересечения и дополнения, здесь – множество всех подмножеств (булеан) универсального множества U.

Теорема. Булева алгебра множеств изоморфна булевой алгебре логических функций .

Изоморфизм означает, что в математическом плане алгебры представляют в своей основе одно и то же. Действительно, аппарат алгебры логики оперирует логическими переменными, которые могут принимать только два значения: 0 и 1. В алгебре множеств вместо одной предметной переменной с введем две логические переменные а и b, определяемые областями множеств соответственно А и В. Пусть переменные принимают два логических значения: 1 – истина, если принадлежат множеству, и 0 – ложь, если не принадлежат множеству. Тогда логические операции над множествами можно описать с помощью таблиц истинности, и наоборот ( табл.).

Таблица

Операции над множествами	Операции над высказываниями	Диаграмма
Объединение	а b 0 0 0 0 1 1 1 0 1 1 1 1
Пересечение	a b 0 0 0 0 1 0 1 0 0 1 1 1
Дополнение A в U	0 1 1 0

В силу изоморфизма любое эквивалентное соотношение в алгебре множеств будет сохраняться в изоморфной ей алгебре высказываний, и наоборот.

Контрольные вопросы

1. Дайте определение логической функции.

2. Дайте определение булевой формуле.

3. Дайте определение булевой алгебре.

4. Приведите примеры булевых алгебр.