Элементы математической логики Лекция 4. Применения языка логики высказываний

4.1 Важнейшие правила следования

4.1.1 Связь отношения логического следования с общезначимостью.

4.1.2 Правила следования, используемые в практике рассуждений

4.2 Анализ рассуждений средствами логики высказываний

4.2.1 Запись предложений естественного языка на язык логики высказываний.

4.2.2 Решение логических задач.

4.1 Важнейшие правила следования

4.1.1 Связь отношения логического следования с общезначимостью.

Th 4.1. ╞В, тогда и только тогда, когда ╞.

В частности, А╞В тогда и только тогда, когда ╞.

Это утверждение доказывается методом от противного.

Следствие 1. ╞В, тогда и только тогда, когда ╞.

Следствие 2. ╞В, тогда и только тогда, когда ╞В.

Применяя к этому следствию Th, получим:

╞В тогда и только тогда, когда ╞.

Th 4.2. а) ╞.

б) Если ╞…,╞

╞ С ,

то ╞ С.

Для сокращения записей обозначим Г любое множество формул, возможно пустое. Тогда первую Th можно сформулировать так:

Г, А╞В тогда и только тогда, когда Г ╞.

Th 4.3. а) Если Г, А╞ С и Г, В╞ С, то Г, АВ╞ С.

б) Если Г╞ АВ и Г, А╞ С и Г, В╞ С, то Г╞ С.

в) Если Г, А╞ В и Г, А╞ ¬В, то и Г ╞ ¬А.

□ а)Пусть Г, А╞ С (*), и Г, В╞ С (**),

но Г, АВ╞ С.

Тогда существует набор значений атомов, входящих хотя бы в одну из формул множества Г{A, В, С}, при котором все формулы множества Г{A, В} имеют значение И, а формула С — значение Л.

Но если при некотором наборе формула АВ имеет значение И, то по определению дизъюнкции значение И имеет хотя бы одна из формул А или В. Если таковой является формула А, то при рассматриваемом наборе все формулы множества Г{A} имеют значение И, а формула С — значение Л, значит

Г, А╞ С., что противоречит условию (*).

Если же значение И имеет формула В, то подобным образом получим противоречие с условием (**).

б), в) доказать самостоятельно. ■

4.1.2 Правила следования, используемые в практике рассуждений

Важнейшие правила следования являются логической основой содержательных дедуктивных рассуждений. Они были сформулированы Генценом под названием правил заключения и позволяют судить о правомерности некоторых следований исходя из правомерности других следований.

Правила заключения Генцена, как и общезначимые формулы, выражают законы логики. В то же время эти правила более естественно, чем общезначимые формулы, отражают способы наших рассуждений.

Одно из этих правил содержится в Th 4.1..

Если Г,А╞ В то Г ╞ (введение импликации, ВИ). (1)

Это правило позволяет вводить импликацию , если доказано следование А╞В, возможно с использованием некоторых других предложений (множество Г). Правило следования ВИ широко используется в доказательствах.

Пусть требуется доказать предложение импликативной структуры . В практике доказательства обычно к тем предложениям, которые уже доказаны (множество Г), добавляется предложение А и, исходя из Г и А, выводится В.

После чего говорят «теорема доказана», т. е. доказана . За этим оборотом и скрывается неявное применение правила ВИ, т. е. переход от следования Г,А╞ В к следованию Г ╞.

Еще два правила следования дает Th 4.3. .

Если Г, А╞ С, и Г, В╞ С, то Г, АВ╞ С. (удаление дизъюнкции, УД) (2)

Согласно правилу УД, для получения следствия С из дизъюнкции АВ достаточно следствие С вывести из А и из В. Другими словами, чтобы вывести С из АВ, эту дизъюнкцию «удаляют» и доказывают два различных следования Г, А╞ С, и Г, В╞ С.

Пункт б) Th 4.3. дает еще один вариант правила УД.

Если Г, А╞ В и Г, А╞ ¬В, то и Г ╞ ¬А. (введение отрицания, ВО) (3).

Правило ВО является логической основой косвенного доказательства (доказательства методом от противного). Чтобы доказать некоторое предложение А, мы допускаем, что А неверно, т. е. верно ¬А и, исходя из ¬А и уже доказанных предложений (множество Г), выводим противоречие В и ¬В (Г, А╞В и Г, А╞ ¬В). После этого говорим «полученное противоречие доказывает теорему». Этот оборот означает неявное применение правила ВО. Действительно, из Г, ¬А╞В и Г, ¬А╞ ¬В по правилу ВО имеем Г╞ ¬¬А, или, применяя правило удаления двойного отрицания (УДО), получим Г╞ А.

Рассмотрим другие правила заключения Генцена, а также некоторые правила, вытекающие из них и часто используемые в практике рассуждений.

Th 4.4. При любом выборе формул А, В, С, D имеют место следующие правила:

4. Если Г╞ А и Г╞ , то Г╞ В) (удаление импликации, УИ, или modus ponens, МР).

5. Если Г╞ А и Г╞ В, то Г╞ АВ (введение конъюнкции, ВК).

6. Если Г╞ АВ , то Г╞ А (первое удаление конъюнкции, УК1).

7. Если Г╞ АВ , то Г╞ В (второе удаление конъюнкции, УК2).

8. Если Г╞ А, то Г╞ АВ (первое введение дизъюнкции, ВД1).

9. Если Г╞ В, то Г╞ АВ (второе введение дизъюнкции, ВД2).

10. Если Г╞ ¬¬А, то Г╞ А (удаление двойного отрицания, УДО).

11. Если Г ╞ и Г ╞, то Г ╞ (силлогизм, С).

12. Если Г ╞ , то Г ╞ ¬B¬A (контрапозиция, К).

13. Если Г╞ ¬В и Г ╞, то Г╞ ¬А (modus tollens, МТ).

Доказательство правил Генцена можно провести разными методами. Покажем их на примере правила МТ.

□ Применим метод от противного к (13).

Пусть Г╞ ¬В (٭), 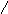Г ╞ (٭٭),

но Г╞ ¬А (٭٭٭).

Тогда должен существовать хотя бы один набор значений атомов формул множества Г{A, В}, при котором все формулы множества Г имеют значение И, а ¬А=Л, значит, А=И. Поэтому из условия (٭٭) В=И, а значит, ¬B=Л. Следовательно, Г╞ ¬В, что противоречит условию (٭).■

Важнейшие правила следования
Логическая операция	Введение	Удаление
	→	→
	→	→
	→	→
	→	→
	→	→