МАТ_ ЛОГИКА / МАТЕМАТИЧЕСКАЯ ЛОГИКА_ЛК9_12_03_2012_Метод резолюций (для высказываний)__

Метод резолюции

Существует эффективный алгоритм логического вывода - принцип (или метод) резолюции Дж. Робинсона. Он показал, что выводимость формулы В из множества посылок и аксиом F₁ F₂, F₃, ..., F_n равносильна доказательству теоремы:

|— (F₁F₂F₃. . . F_nB),

|— (­(F₁F₂F₃. . . F_n)B),

Из того, что (­(F₁F₂F₃. . . F_n)B)=И следует, что

(F₁F₂F₃...F_n (B))=Л.

Так как (F₁F₂F₃...F_n  (B)) есть КНФ, то все F_i и B должны быть приведены к КНФ. Множество элементарных дизъюнктов (входящих в КНФ): К={D₁, D₂, ..., D_m}. Два дизъюнкта D_i и D_j , содержащие одинаковые пропозициональные переменные, но с противоположными знаками, объединяют в третий дизъюнкт D_k=(D_iD_j) – резольвенту, из которой удаляются эти переменные. Пропозициональные переменные с противоположными знаками называют контрарными атомами. Если D_i=А, D_j=A, то D_k=(D_iD_j)=(АA) есть пустая резольвента, которую обозначают символом . Многократно применяя процедуру объединения дизъюнктов множества К с контрарными атомами стремятся получить пустую резольвенту. Наличие пустой резольвенты означает, что выводима формула

|— (­(F₁F₂F₃. . . F_n)B).

Алгоритм вывода по методу резолюции:

Шаг 1: принять отрицание заключения, т.е. В,

Шаг 2: привести все формулы посылок и отрицания заключения в конъюнктивную нормальную форму,

Шаг 3: выписать множество дизъюнктов всех посылок и отрицания заключения: К = {D₁ D₂, ..., D_k },

Шаг 4: выполнить анализ пар множества К по правилу: «если существуют дизъюнкты D_i и D_j, один из которых (D_i) содержит атом А, а другой (D_j) - атом А, то соединить эту пару логической связкой дизъюнкции (D_iD_j) и сформировать новый дизъюнкт - резольвенту, исключив контрарные атомы А и А, а резольвенту включить в множество К»,

Шаг 5: если в результате соединения дизъюнктов получена пустая резольвента (пустой дизъюнкт), то конец (доказательство подтвердило истинность заключения), иначе включить резольвенту в множество дизъюнктов К и перейти к шагу 4 (по закону идемпотентности любой дизъюнкт и любую резольвенту можно использовать неоднократно, т.е. из множества К не следует удалять использованные в соединении дизъюнкты).

Многие правила (modus ponens, транзитивность и др.) – частные проявления правила резолюции. В таблице слева приведены названия, в центре – традиционные формы известных правил вывода, справа – те же самые правила, записанные в обозначениях метода резолюции.

Название правила	Традиционная форма	Резолютивная форма
Modus ponens
Транзитивность
Слияние

Пример Доказать истинность заключения для правила Modus ponens

по методу резолюции.

Вывод по методу резолюции:

А – первая посылка содержит один дизъюнкт,

- вторая посылка содержит один дизъюнкт,

¬В - отрицание заключения содержит один дизъюнкт.

Множество дизъюнктов:

K={А, (AB), В}.

(AB) В≡A – резольвента.

Множество дизъюнктов:

K₁={А, (AB), В, A}.

AА≡ - пустая резольвента.

Пример Доказать истинность заключения для правила

по методу резолюции.

Вывод по методу резолюции:

- первая посылка содержит один дизъюнкт,

- вторая посылка содержит один дизъюнкт,

- отрицание заключения содержит два дизъюнкта А и ¬С.

Множество дизъюнктов:

K={(AB), (ВС), А, С}.

(AB) (ВС )≡(AС) – резольвента.

Множество дизъюнктов:

K₁={(AB), (ВС), А, С, (AС)}.

С(AС) ≡A – резольвента.

Множество дизъюнктов:

K₂={(AB), (ВС), А, С, (AС), A}.

AА≡ - пустая резольвента.

Пример Доказать истинность заключения по методу резолюции: (ABC),(CD M), (NDM)

(ABN)

Вывод по методу резолюции:

ABC ( AB)C  (ABC) – первая посылка содержит один дизъюнкт,

CDM (CD)M  (CDM) – вторая посылка содержит один дизъюнкт,

NDM NDM  (ND)  (NM) – третья посылка содержит два дизъюнкта,

((AB) N)  ABN - отрицание заключения содержит три однолитерных дизъюнкта,

Множество дизъюнктов:

K={(ABC), (CDM), (ND), (NM), А, В, N},

(MN)N  М - резольвента,

Множество дизъюнктов:

K₁={(ABC), (CDM), (ND), (NM), А, В, N, М},

(CDM)M  (CD) - резольвента,

Множество дизъюнктов:

K₂={(ABC), (CDM), (ND), (NM), А, В, N, М, (­C­D)},

(­¬A¬­BC)  (­¬C­¬D)  (­¬A¬­B­¬D) - резольвента,

Множество дизъюнктов:

K₃={(ABC), (CDM), (ND), (NM), А, В, N, М, (­C­D), (¬A¬B­¬D)},

(­¬A­¬B­¬D) A  (­¬B­¬D) - резольвента,

Множество дизъюнктов:

K₄={(ABC), (CDM), (ND), (NM), А, В, N, М, (­C­D), (¬A¬B­¬D), (­¬B­¬D)},

(­¬B­¬D)B  ­¬D - резольвента,

Множество дизъюнктов:

K₅={(ABC), (CDM), (ND), (NM), А, В, N, М, (­C­D), (¬A¬B­¬D), (­¬B­¬D),  D},

D (ND)  N - резольвента,

Множество дизъюнктов:

K₆={(ABC), (CDM), (ND), (NM), А, В, N, М, (­C­D), (¬A¬B­¬D), (­¬B­¬D),  D, N},

N­N   - пустая резольвента, что и требовалось доказать.

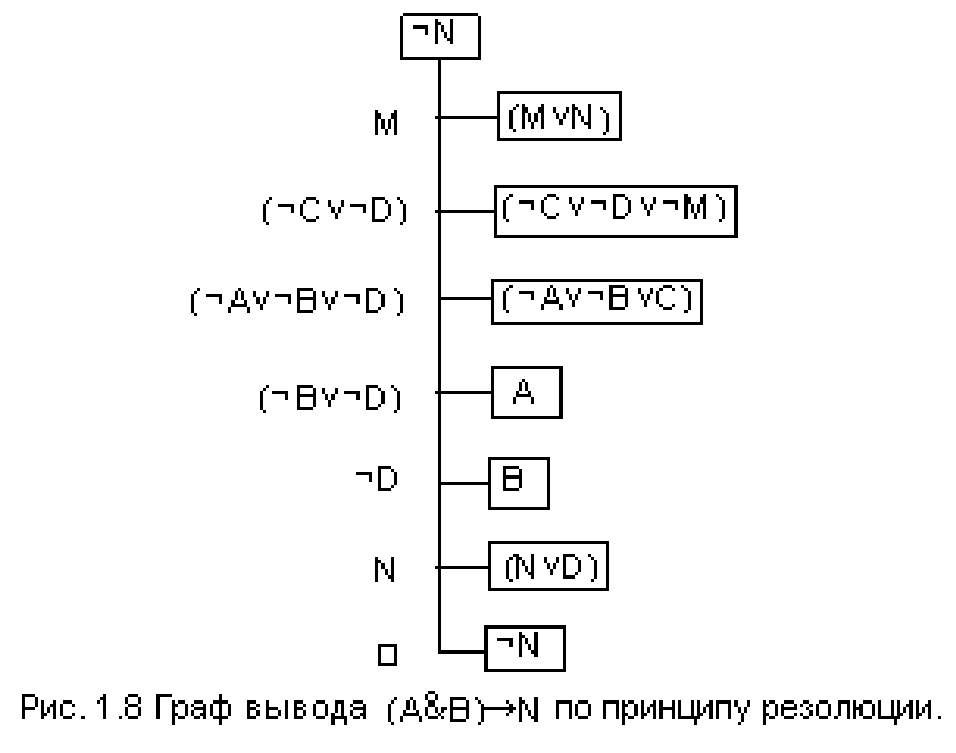
Рис. 1. Граф вывода (ABN) по принципу резолюции.

Для демонстрации удобно использовать граф типа дерево, корнем которого является один из дизъюнктов отрицания заключения, а листьями- дизъюнкты всех посылок и отрицания заключения. Тогда узлами графа являются резольвенты. На рис. 1. показан граф вывода этой задачи.

Пример Доказать истинность заключения:

(А В)  (С  D), (D  В  М), ­М

(­A­C)

Вывод по методу резолюции:

(AB)  (CD)  (­AB)  (­CD) - посылка,

DBM  ­(DB)M  (­D­BM) - посылка,

­M - посылка,

­ (­A­C ) = AC - отрицание заключения,

Множество дизъюнктов:

К ={А, С, ­М, (­AB), (­CD), (­D­BM)},

A (­AB)  В - резольвента,

Множество дизъюнктов:

К₁ ={А, С, ­М, (­AB), (­CD), (­D­BM), В},

B(­D­BM)  (­DM) - резольвента,

Множество дизъюнктов:

К₂ ={А, С, ­М, (­AB), (­CD), (­D­BM), В, (­DM)},

(­­DM)  (­­CD)  (­­CM) - резольвента,

Множество дизъюнктов:

К₃ ={А, С, ­­М, (­­AB), (­­CD), (­­D­­BM), В, (­­DM), (­­CM)},

(­­CM) ­­M  ­­C - резольвента,

­­CC   - пустая резольвента, ч.т.д.

На рис. 2 показан граф вывода этой задачи.

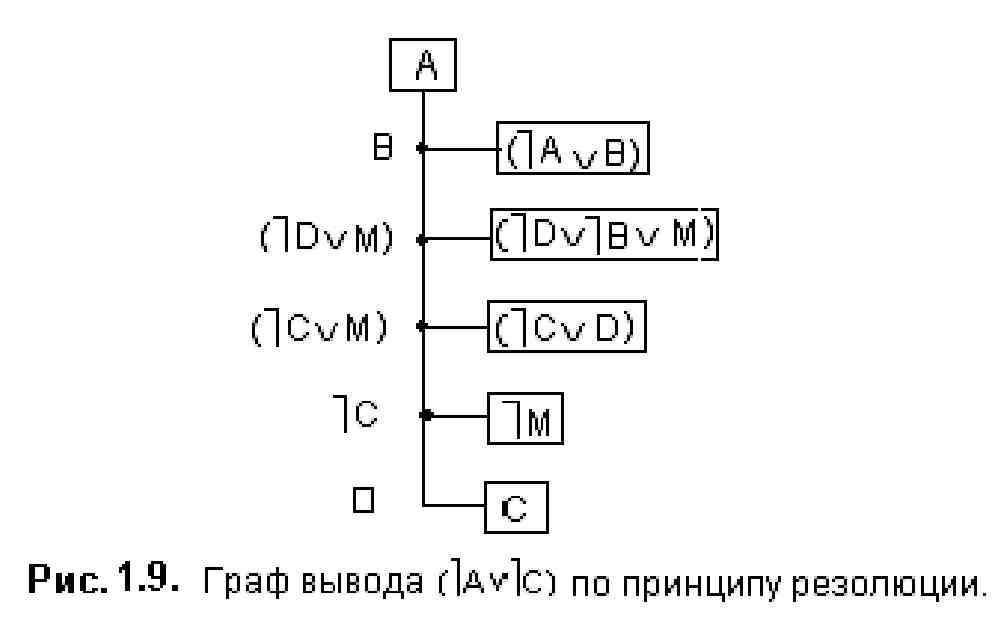
Рис.2. Граф вывода (­A­C) по принципу резолюции.

Пример. Работа автоматического устройства, имеющего три клапана А, В и С, удовлетворяет следующим условиям: если не срабатывают клапаны А или В или оба вместе, то срабатывает клапан С; если срабатывают клапаны А или В или оба вместе, то не срабатывает клапан С. Следовательно, если срабатывает клапан С, то не срабатывает клапан В.

Доказать истинность заключения:

((¬­А­¬В­¬АВ) С), ((АВАВ)  С)

(С  ­В)

Вывод по методу резолюции:

(­¬А­¬B­¬А­¬B) С  (­¬А(­¬B­¬А)­¬B) С =

=­ ¬ (­¬А(­¬B­¬А)­¬B) С=­­¬¬А¬ ­ ((­¬B­¬А)­¬B)) С=

=А (­ ¬ (¬­B­¬А) ¬¬­­B))С=А((BА)B))С=АBС=(АC)(BC) – первая посылка, содержит два дизъюнкта: (АC) и (BC);

(ABАB) ¬ ­C  (­А­C)  (­B­C) – вторая посылка, содержит два дизъюнкта:

(­А­C) и (­B­C);

¬(CВ)=¬(¬CВ)=¬¬C¬¬В=CВ - отрицание заключения, содержит два дизъюнкта: С и В.

Множество дизъюнктов:

K={(АC), (BC), (­А­C), (­B­C), С, В}.

С(­В­C) = ­В - резольвента,

множество дизъюнктов:

K₁={(АC), (BC), (­А­C), (­B­C), С, В, ­В},

­ВВ =  - пустая резольвента.

Доказано, что если срабатывает клапан С, то не срабатывает клапан В.

Пример. Доказать истинность заключения

A; В; (СAB)

С.

1) A - посылка;

2) B - посылка;

3) CA B = (CAB) - посылка;

4) (C) = C - отрицание заключения;

5) множество дизъюнктов: K={A; B; (CAB); C};

6) A(CAB)=(СB) - резольвента из 1) и 3);

7) K₁={A; B; (CAB); C; (СB)};

8) B(СB)=C - резольвента из 2) и 6);

9) K₂={A; B; (CAB); C; (СB); C };

10) СC = - пустая резольвента из 4) и 7).

1)-10) - доказательство истинности заключения  C по принципу резолюции.

Пример. Доказать истинность заключения

(AB)(CD); (DBM);¬ M

(¬A¬C)

1) (AB)(CD)=( ¬AB)( ¬CD) - посылка;

2) DBM=¬ (DB)M=(¬D¬BM) - посылка;

3) ¬ M - посылка;

4) ¬( ¬ A ¬ C ) = A  C - отрицание заключения;

5) K ={A; C; ¬M; (¬AB); (¬CD); (¬D¬BM)}

6) A(¬AB)=B - резольвента;

7) B(¬D¬BM)=( ¬DM) - резольвента;

8) (¬DM)( ¬CD)=( ¬CM) - резольвента;

9) (¬CM) ¬M=¬C - резольвента; 10) ¬CC= - пустая резольвента.

1)-10) - доказательство истинности заключения (¬A¬C).

Достоинством принципа резолюции является то, что при доказательстве применяют только одно правило: поиск и удаление контрарных атомов дизъюнктов, а для этого механизм вывода использует правила подстановки и унификации дизъюнктов.