y ' = 1 ( a – 2 x )2 + x 2( a – 2 x ) (-2) = ( a – 2 x )( a – 2 x – 4 x )=
= ( a – 2 x )( a – 6 x ).
Находим критические точки. Производная равна нулю при x 1 = а2 и x 2 = а6 .
Находим значения функции в критических точках и на концах отрезка:
|
а |
|
а |
2 |
a 3, f(0) = 0. |
|
|
|||||
f |
|
= 0; |
f |
|
= |
|
|
|||||
|
|
27 |
|
|
||||||||
|
2 |
|
6 |
|
а |
|
|
2 |
|
|||
Итак, наибольшее значение функции M = f |
|
= |
a 3. |
|||||||||
|
|
|
|
|
|
|
6 |
|
|
27 |
|
|
Если сторона вырезаемых квадратов x = а6 , получим короб-
ку наибольшего объёма
y = 2 a 3.
27
4.4. Выпуклость графика функции. Точки перегиба
Определение. График дифференцируемой функции
y = f(x) называется выпуклым вверх на интервале (а, b), если все точки графика лежат ниже любой касательной к графику функции на этом на интервале (рис. 28). График дифференцируемой функции y = f(x) называется выпуклым вниз на интервале (а, b), если все точки графика лежат выше любой касательной к графику функции на этом интервале (рис.29).
Рис. 28
51
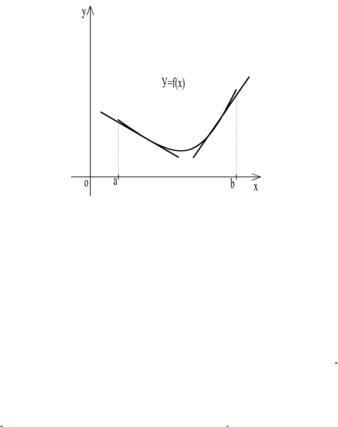
Рис. 29
Теорема. Достаточный признак выпуклости.
Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый вверх. Если во всех точках интервала (a, b) вторая производная функции f(x) положительна, т.е.
f ''(x)>0, то график функции на этом интервале выпуклый вниз.
Пример 6. Доказать, что график функции y = x arctgx
везде выпуклый вниз.
Решение. Находим первую и вторую производные:
y' = (x arctgx)' = (x)' arсtgx + x(arсtgx)' = 1 arctg x + |
|
x |
; |
|||||
|
1 + x2 |
|||||||
|
x ′ |
1 |
|
x'(1+ x2 )− x(1+ x2 )' |
|
|
|
|
y" = arctgх+ |
|
= |
|
+ |
|
= |
|
|
|
1+ x2 |
(1+ x2 )2 |
|
|||||
|
1+ x2 |
|
|
|
|
|||
= |
|
1 |
+ |
1+ x2 |
−2x2 |
= |
1+ x2 |
+1− x2 |
= |
|
2 |
> 0. |
||||
|
+ x2 |
|
(1 |
+ x2 )2 |
|
(1 |
+ x2 )2 |
|
+ x2 )2 |
|||||||
1 |
|
|
(1 |
|
||||||||||||
Следовательно, по достаточному признаку график функции выпуклый вниз при x (−∞,+∞).
Определение. Точка, отделяющая выпуклую вверх часть графика непрерывной функции от выпуклой вниз, называется
точкой перегиба графика функции.
52
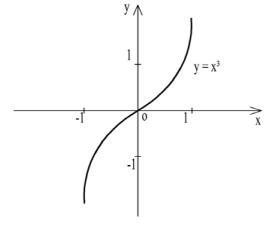
На рис. 30, 31, 32 точки О, А – точки перегиба.
Если в точке перегиба существует касательная к графику, то график функции с одной стороны от точки перегиба лежит над касательной, а с другой стороны – под касательной (рис. 30, 31).
Рис. 30
Теорема. Необходимый признак точки перегиба.
Если х0 – абсцисса точки перегиба графика функции y = f(x), то вторая производная f "(x0) равна нулю или не существует.
Замечание 1. Таким образом, абсциссы точек перегиба графика функции следует искать среди точек, в которых вторая производная равна нулю или не существует.
Замечание 2. Равенство f "(x0) = 0 является необходимым, но не достаточным признаком точки перегиба функции, имеющей вторую производную. Рассмотрим, например, функцию y = x4. Найдём производные: y' = 4x3, y " = 12x2 = 0 при х = 0.
Однако точка О (0; 0) не является точкой перегиба (рис. 33).
53
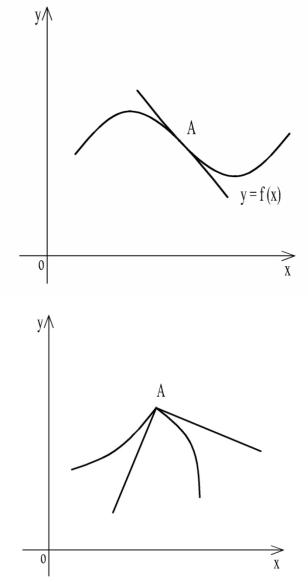
Рис. 31
Рис. 32
54
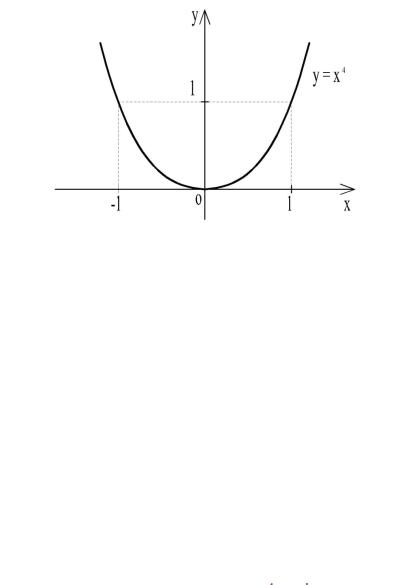
Рис. 33
Теорема. Достаточный признак точки перегиба.
Пусть функция y=f(x) непрерывна в точке х0, имеет вторую производную в некоторой окрестности точки х0, за исключением, быть может, самой точки х0. Если при переходе через точку х0 вторая производная f ''(х) меняет знак, то точка графика функции М (х0, f(x0)) – точка перегиба.
Доказательство. Так как вторая производная f ′′(x) слева и справа от точки x0 имеет разные знаки, то направление выпуклости графика функции слева и справа от точки x0 различны. Но тогда, по определению, точка графика функции M (x0 , f (x0 )) −
точка перегиба.
Пример 7. Найти точки перегиба и интервалы выпуклости вверх и вниз графика функции y=x3-3x2-12x+3.
Решение. Находим производные: y=3x2-6x-12, y"=6x-6. Вторая производная обращается в нуль при x0=1. Так как f "(x)<0 при x<1, то график функции выпуклый вверх на интервале
(-∞, 1). Так как f "(х)> 0 при х>1, график функции выпуклый вниз на интервале (1,+∞). Следовательно, х0=1 – абсцисса точки перегиба. Найдем ординату y0 =13-3 12-12 1+3=-11. Точка
M(1,-11) – точка перегиба графика функции.
55