§2.13. Гіпербола.

Гіперболою називається множина точок площини, які мають наступні властивості: модуль різниці відстаней від будь-якої точки цієї множини до двох заданих точок площини є величина стала, менша за відстань між даними точками і відмінна від нуля. Дві дані точки називаються фокусами гіперболи і позначаються і .

Уведемо позначення: – відстань між фокусами F₁ і F₂; – модуль різниці відстаней від довільної точки гіперболи до фокусів ( ). Систему координат задаємо так, щоб фокуси гіперболи знаходилися на осі і були симетричними відносно осі (рис.11). У відповідності з означенням, можемо записати

. (13.1)

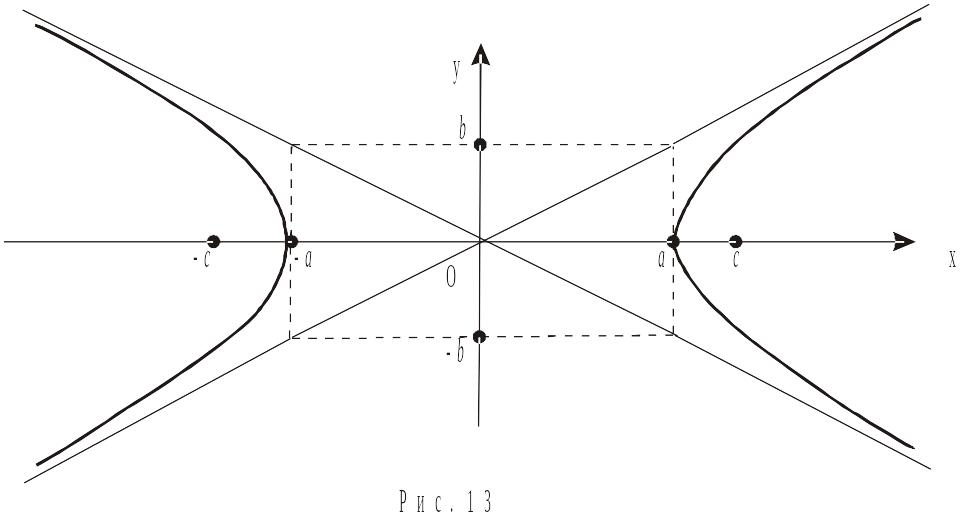
На основі (13.1), дістанемо канонічне рівняння гіперболи

, (13.2)

де . Використовуючи останнє рівняння, будуємо криву (рис.13). Величини і ( і ) називаються відповідно дійсною й уявною осями (півосями) гіперболи.

Якщо фокуси гіперболи розміщені на осі симетрично відносно осі , то канонічне рівняння гіперболи має вигляд

, (13.3)

де . У цьому випадку і – відповідно уявна й дійсна осі.

Ексцентриситетом гіперболи називається відношення відстані між фокусами до дійсної осі, тобто або . Для гіперболи .

Асимптотою кривої називається пряма, яка має наступну властивість: відстань від точки кривої до цієї прямої нескінченно зменшується при нескінченому віддаленні точки кривої від початку координат. Гіпербола має дві асимптоти (рис.13):

, . (13.4)

Приклад 1. Гіпербола задана рівнянням .

Знайти: а) півосі гіперболи; б) фокуси; в) ексцентриситет; г) рівняння асимптот.

Розв’язання. а) Після ділення даного рівняння на 36, маємо

.

Отже, , .

б) Для гіперболи , ; , – фокуси гіперболи.

в) Так як – дійсна піввісь, то .

г) застосовуючи формули (13.4), знайдемо рівняння асимптот: , .

Еліпс і гіпербола є центральними кривими, тобто вони мають центр симетрії (для канонічних рівнянь – початок координат).Окрім того, ці криві мають по дві осі симетрії (для канонічних рівнянь – осі координат).

§2.14. Парабола.

Параболою називається множина точок площини, кожна з яких рівновіддалена від даної прямої і даної точки, що не лежить на цій прямій. Дана пряма називається директрисою, а дана точка – фокусом. Якщо відстань між фокусом і директрисою позначити через , одну з координатних осей провести через фокус перпендикулярно до директриси, а іншу – посередині між фокусом і директрисою (на відстані від фокуса й директриси), то отьримаємо одне з канонічних рівнянь параболи:

, , , (14.1)

На основі формул (14.1) легко побудувати самі криві (рис.14).

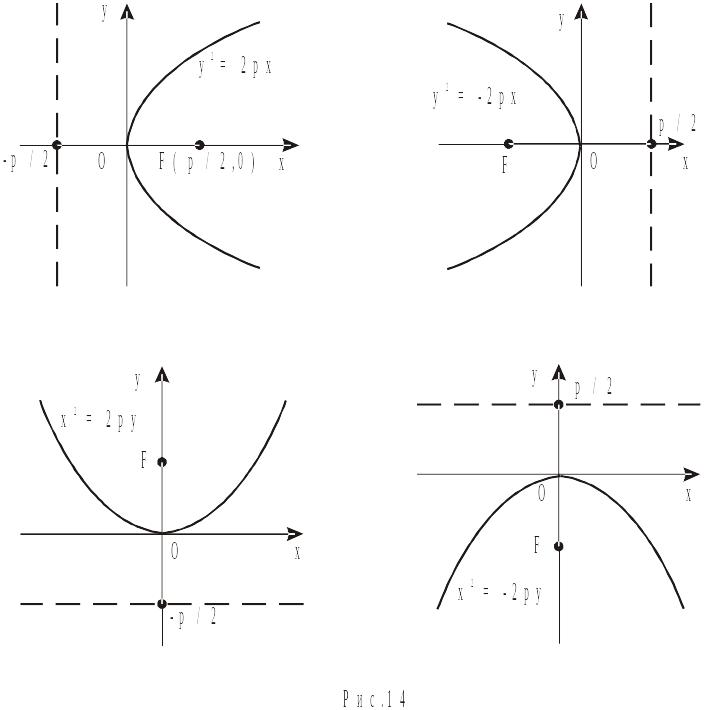
Як бачимо, парабола, а, отже і її основні характеристики визначаються одним параметром . Наприклад, і є відповідно рівнянням директриси й точкою фокуса параболи, яка описується першим із рівнянь (14.1).

Приклад 1. Парабола задана рівнянням . Визначити параметри , рівняння директриси й координати фокуса цієї параболи.

Розв’язання. дане рівняння відповідає загальній формулі . Отже, ; – рівняння директриси; – точка фокуса.