§ 2.3. Лінійні операції над векторами.

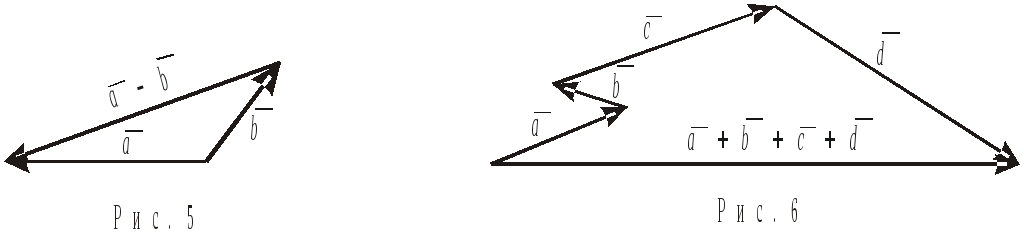
Операції додавання, віднімання векторів і множення вектора на число називаються лінійними операціями над векторами. Додавати два вектори можна за правилом паралелограма (рис.3) або за правилом трикутника (рис.4).

Операція віднімання векторів визначається рівністю

, (3.1)

де – вектор, протилежний до вектора .

На основі формули (3.1) операція віднімання зводиться до операції додавання двох векторів. Різницю двох векторів можна знаходи-ти, також, за правилами трикутника (рис. 5). При додаванні декількох векторів зручно використовувати правило многокутника (рис.6).

Добутком додатної (від’ємної) сталої k на вектор є вектор =k , який однаково (протилежно) напрямлений з вектором і модуль якого дорівнює (якщо , то довжина вектора збільшується у |k| раз; якщо , то довжина вектора зменшується у 1/|k| раз).

Приклад 1. Нижче для заданих векторів , , побудовано вектор

Основні властивості лінійних операцій (k, l –числа):

1) 2)

3) 4) ;

5) 6)

7) , , .

Якщо вектори задані своїми координатами, то при додаванні (відніманні) двох векторів їхні відповідні координати додаються (віднімаються). Для того щоб помножити вектор на число, на це число необхідно помножити всі координати даного вектора. Для векторів (a_x, a_y, a_z), (b_x, b_y, b_z) і сталої k можемо записати

, (3.2.)

, (3.3.)

(3.4.)

Приклад 2. Задані вектори (2;0;5), (3;1;-2) і (-1;1;0). Знайти вектор .

Розв’язання. Використовуючи властивості лінійних операцій (розкриваємо дужки і зводимо подібні за звичайними правилами), маємо:

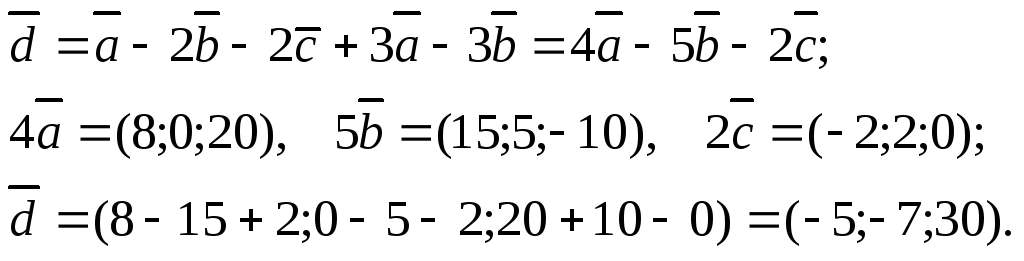
§ 2.4. Лінійна залежність векторів. Базис.

Нехай у просторі задані три ненульових вектори і . Якщо рівність

(4.1.)

м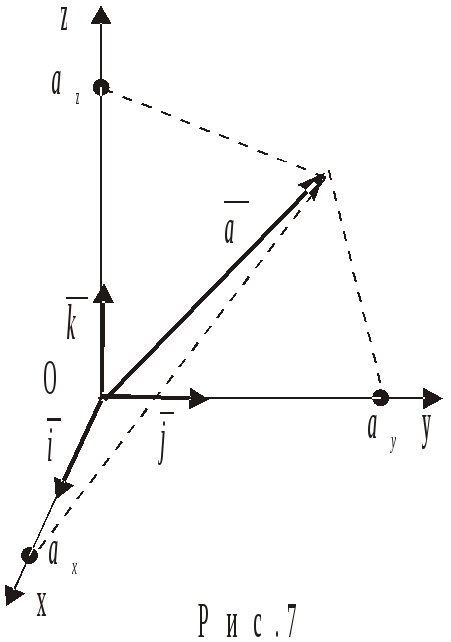 ожлива тільки при , то кажуть, що вектори , і лінійно незалежні. Якщо існує трійка чисел , серед яких хоча б одне відмінне від нуля і для яких виконується рівність (4.1.), то вектори , лінійно залежні. В останньому випадку один із трьох векторів може бути представлений через лінійну комбінацію двох інших, наприклад, .

Якщо ненульові вектори і лінійно незалежні, то упорядкована трійка цих векторів є базисом у просторі. Будь–який інший вектор може бути представлений через лінійну комбінацію базисних векторів:

. (4.2.)

Упорядкована трійка чисел називається координатами вектора у базисі , .

Координати вектора, що були визначені у §2.2. є його координатами у ортонормованому базисі , , (рис.7). Напрями останніх векторів співпадають із напрямками координатних осей, а їхні довжини дорівнюють одиниці, тобто . Іншими словами, якщо вектор представлений у вигляді

, (4.3.).

то упорядкована трійка чисел а_х , а_у , а_z є його координатами, які були визначені у § 2.2. Надалі координати вектора часто будуть задаватися у формі (4.3).

Нехай вектори задані своїми координатами у базисі (цей базис взято для визначеності; можна було взяти будь-який інший):

, ,

, .

Визначимо умову, при якій вектори утворюють базис і знайдемо координати вектора у цьому базисі.

Перепишемо векторну рівність (4.1.) у координатній формі:

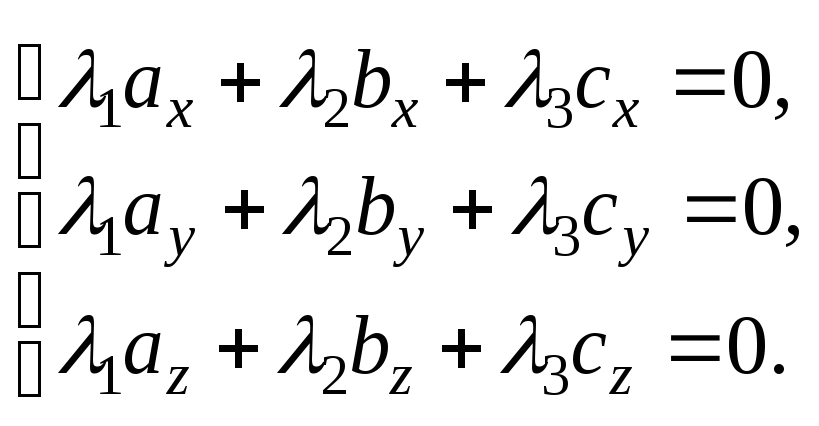(4.4)

Однорідна система (4.4) має єдиний нульовий розв’язок (див. § 1.7) при умові, що визначник системи відмінний від нуля:

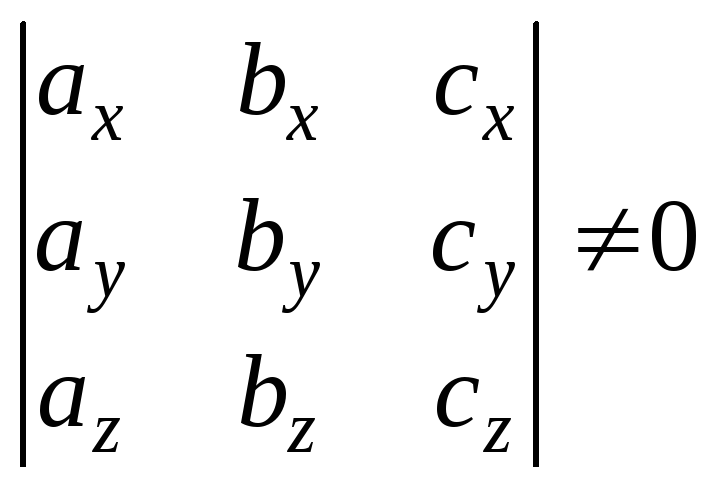. (4.5)

Нерівність (4.5) і є шуканою умовою того, що вектори утворюють базис.

Припустимо, що умова (4.5) виконується. Знайдемо координати вектора у базисі . Перепишемо рівність (4.2) у координатній формі:

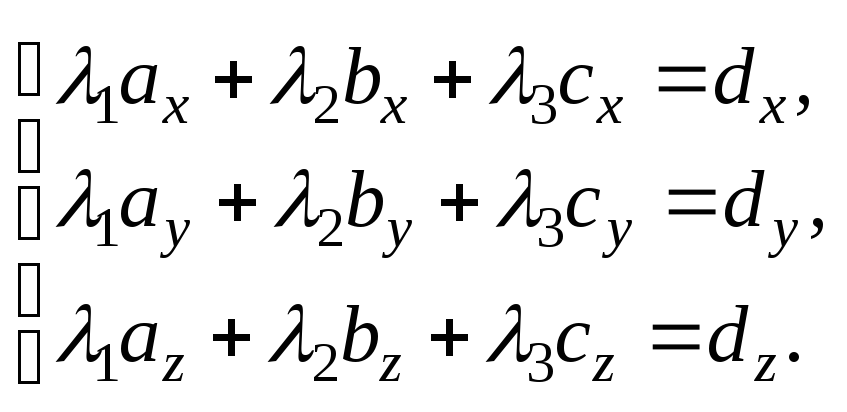(4.6)

Розв’язавши невироджену систему (4.6) будь-яким методом, знайдемо координати .

Приклад 1. Вектори , , , і задані у деякому базисі. Довести, що вектори утворюють базис і знайти координати вектора у цьому базисі.

Розв’язання. Доведемо, що вектори утворюють базис (перевіримо умову (4.5)):

.

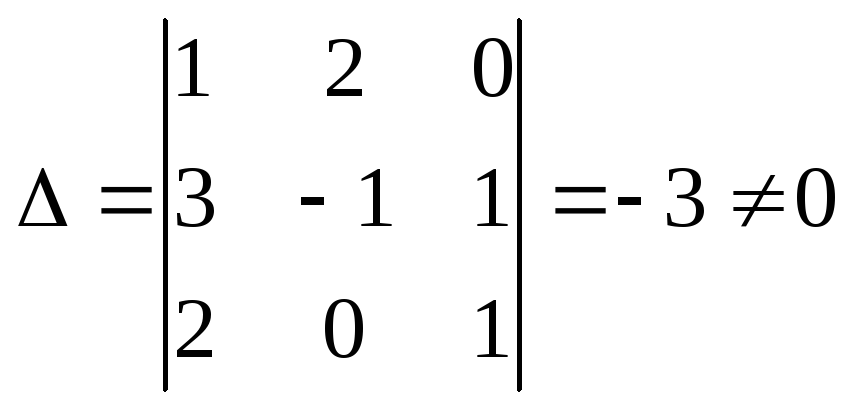Запишемо систему (4.6):

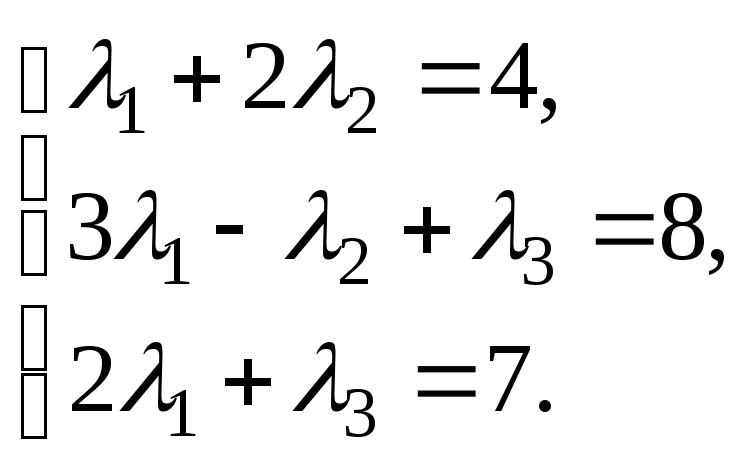
Розв’язуємо систему за формулами Крамера: , , ; , ,

Отже, .